| acmsguru |
|---|
| Закончено |
→ Теги задачи
Нет тегов
Нет прав на редактирование
Условие задачи было недавно изменено. Просмотреть изменения.
×
549. Dumbbells
Time limit per test: 1 second(s)
Memory limit: 262144 kilobytes
Memory limit: 262144 kilobytes
input: standard
output: standard
output: standard
A sports shop has n dumbbells in store. Each of them is characterised by its mass mi and cost ci. Recently the shop manager faced the following non-trivial problem. He has to find the maximum number of sports sets that satisfy the following requirements:
- each set must contain exactly k dumbbells;
- each set must have dumbbells of k distinct masses;
- for each pair of sets the masses of dumbbells must coincide
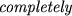 , that is, the masses in the sets must be equal as
, that is, the masses in the sets must be equal as 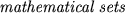 .
.
The manager's task is to make the maximum number of such sets. If there are several ways to make the maximum possible number of sets, he should choose the one that has the maximum total cost of dumbbells that are contained in the chosen sets. Note that the primary goal is to maximize the number of sets and maximization of the total cost is the secondary goal.
Input
The first line of the input contains integers n and k (1 ≤ n,k ≤ 4000). Next n lines contain descriptions of the dumbbells, one per line. Each description consists of a pair of integers mi, ci (1 ≤ mi,ci ≤ 4000), mi is the mass of the i-th dumbbell, and ci is its cost.Output
In the only output line print two integers — t and s, where t is the maximum number of sets, and s is the maximum total cost of dumbbells in t choosen sets. If the manager can't make at least one set, print a pair of zeroes.Example(s)
sample input | sample output |
7 2 16 1 4 6 16 7 7 100 32 9 4 6 32 1 | 2 22 |
sample input | sample output |
4 2 1 2 2 1 4 3 1 7 | 1 10 |
Note
In the first sample the manager should make two sets. One of the possible solutions is as follows: the first set contains the second and the seventh dumbbells, the second set contains the fifth and the sixth dumbbells.In the second sample the manager can make only one set. It consists of the third and the fourth dumbbells.
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 00:37:23 (k2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|




