Благодарности

Прежде чем перейти к разбору задач, я хотел бы поблагодарить всех, кто помогал делать отборочные раунды Russian Code Cup.

Члены жюри, авторы и разработчики задач:

• Виталий Аксенов Aksenov239
• Артем Васильев VArtem
• Николай Ведерников Niko
• Виталий Демьянюк chavit
• Андрей Комаров komarov
• Георгий Корнеев
• Павел Кротков pashkal
• Демид Кучеренко BLIZZARD
• Анна Малова
• Борис Минаев qwerty787788
• Андрей Станкевич andrewzta

Координатор разборов Виталий Аксенов Aksenov239

Прорешивали раунды:

• Геннадий Короткевич tourist
• Павел Маврин pashka
• Нияз Нигматуллин niyaznigmatul
• Владимир Смыкалов enot110
• Дмитрий Филиппов DimaPhil
• Сергей Цаплин Sert

Разумеется, те, кто участвовал в чемпионате, прорешивали только раунды, в которых они не могли участвовать.

Задача A. Разбор задач.

Идея: Анна Малова.
Реализация: Андрей Комаров.
Разбор: Андрей Комаров.

В задаче требуется составить план разбора задач так, чтобы суммарная продолжительность разбора была минимальной. Задачи должны разбираться в порядке с первой до m-й. Время разбора одной задачи состовляет t секунд. Замена разбирающего задачу члена жюри — c секунд. Если один и тот же член жюри разбирает несколько задач подряд, то замена не требуется. Про каждого члена жюри известно, какие задачи он хочет разбирать, а какие — нет.

Эта задача решается жадным алгоритмом. Выберем члена жюри, который умеет решать максимальное число задач, начиная с первой. Пусть он умеет решать k задач. Затем, выберем того, кто умеет решать максимальное число задач начиная с k-й. Будем продолжать так, пока не будут разобраны все задачи. Тогда ответом на задачу будет m · t + q · c, где q — число произведённых замен.

Почему это является оптимальным ответом? Пусть в какой-то момент был выбран член жюри, желающий проводить разбор не максимального числа задач. Тогда, от того, что его заменят на того, кто умеет разбирать больше и дать ему разобрать больше, ответ может только улучшиться.

Данное решение работает за O(n·m).

Также можно было написать простое решение с помощью динамического программирования. dp[i][j] равно минимальному времени, которое тратится, если разобрали i задач и i-ую разбирал j-ый член жюри. Данный массив можно легко посчитать за O(n²m).

Задача B. На далекой Амазонке.

Идея: Виталий Аксенов.
Реализация: Демид Кучеренко.
Разбор: Демид Кучеренко.

В данной задаче необходимо построить ориентированный граф, состоящий из n вершин, в котором выполняются следующие условия:

• В графе не должно быть циклов
• В каждую вершину ведёт максимум одно ребро
• В графе должно быть ровно a вершин, из которых существовуют исходящие ребра
• В графе должно быть ровно b вершин, в которые существуют входящие ребра

Для начала разберем случаи, когда ответ «IMPOSSIBLE». Это случаи, когда выполняется хотя бы одно из условий:

• Матерей больше, чем дочерей
• Матерей больше, чем n-1 (все матерьми быть не могут)
• Дочерей больше, чем n-1

Если такой граф возможно построить, то сначала построим цепочку из a ребер (Таким образом у нас будет задействованы a+1 женщина, и будет a матерей и a дочерей). После чего, дополним дочерьми любых матерей, чтобы дочерей стало ровно b. Может получиться так, что некоторые женщины не будут ни матерьми, ни дочерьми, но это не противоречит условию задачи.

Задача C. Лабораторная по физике.

Идея: Виталик Аксенов.
Реализация: Артем Васильев.
Разбор: Артем Васильев.

В данной задаче требуется определить, какую температуру воды можно получить при смешивании воды из двух сосудов с холодной и горячей водой. Требовалось отвечать на несколько таких запросов при заданной температуре.

Запишем формулу температуры воды, если мы смешиваем холодную воду из сосуда объёмом c_i и горячую воду из сосуда объёмом h_j: T = p / q = (C·c_i + H·h_j) / (c_i + h_j) Преобразовав эту формулу, получим, что (H·q — p) / (p — C·q) = c_i / h_j Таким образом, мы свели задачу к следующей: задана несократимая дробь и множество числителей и знаменателей, можно ли выбрать числитель и знаменатель так, чтобы получилась заданная дробь?

Введем обозначения A_x — множество всех c_i / x, где c_i делится на x. Аналогично, B_y — множество всех h_i / y, где h_i делится на y. Тогда несократимую дробь p / q можно представить тогда и только тогда, когда A_p и B_q пересекаются. Стоит отметить, что суммарный размер всех множеств A_x и B_y равен O(M log M), где M — ограничение на объем сосудов (в данной задаче M равно 10⁵).

При представлении A_x и B_y в виде отсортированных списков один запрос можно выполнить за O(M / max(x, y)). Если представлять A_x и B_y как битовые множества, то получается решение за O(M / 64) на запрос.

Самое быстрое решение получается, если не считать ответы для одной и той же дроби несколько раз. В этом случае можно доказать более точную оценку на время работы решения. Докажем оценку O((M + k) sqrt(M)), где k — количество запросов. Если максимум из p и q больше, чем sqrt(M), то запрос можно выполнить за O(sqrt(M)), просмотрев все элементы меньшего из множеств.

Оценим сумму времен выполнения всех остальных запросов. Запросов, выполняющихся за O(M / x) не больше, чем 2x. Cуммируя по всем x, и учитывая, что x не больше, чем sqrt(M), получаем оценку O((M + k) sqrt(M)) Суммарное время работы решения: O((M + k) sqrt(M)).

Задача D. Конструктор пил.

Идея: Николай Ведерников.
Реализация: Николай Ведерников.
Разбор: Николай Ведерников.

В задаче требуется посчитать количество перестановок, таких что:

• a_2·i-1≤ a_2·i
• a_2·i ≥ a_{2·i + 1}

Заметим, что количество таких перестановок равно количеству перестановок, у которых на нечётных позиция стоят числа, больше своих соседей. Биективное соответствие: b_i = n — a_i. Назовём такую перестановку убывающей пилообразной. Это нам пригодится дальше для решения задачи.

Очевидно, что если длина перестановки равна 0 или 1, то ответ — 1.

Пусть мы знаем ответ для всех длин от 0 до n, найдём ответ для n+1. Будем считать общее количество пилообразных последовательностей. Для того чтобы получить количество возрастающих, нужно общее число последовательностей разделить на 2, так как количество возрастающих равно количеству убывающих.

Пусть n+1 поставили на позицию 2·k, тогда сначала у нас идёт возрастающая пилообразная длиной 2·k−1, а после возрастающая длиной n−2·k+1. На первые 2·k−1 позиций мы можем выбрать любые из n чисел. Итого, получаем, что количество перестановок длины n+1, у которых число n+1 на позиции 2·k: ans_2·k−1 · ans_n−2·k+1 · Binom(n, 2·k−1).

Пусть n+1 поставили на позицию 2·k+1, тогда сначала у нас идёт убывающая пилообразная длиной 2·k, а после возрастающая длиной n−2·k. На первые 2·k позиций мы можем выбрать любые из n чисел. Итого получам, что количество перестановок длины n+1, у которых число n+1 на позиции 2·k+1: ans_2·k · ans_n−2·k · Binom(n, 2·k).

Итого, общее число пилообразных последовательностей длины n+1: ans_n+1 = ∑ⁿ_{k = 0} ans_k · ans_n−k · Binom(n, k).

Задача E. Зарплата.

Идея: Анна Малова.
Реализация: Павел Кротков.
Разбор: Павел Кротков.

В данной задаче дан ориентированный граф. Все ребра можно было классифицировать на три части.

• при любой расстановке окладов и бонусов в вершинах этого ребра условие руководства будет выполняться
• для выполнения условия руководства необходимо или поменять оклад с бонусом в обеих вершинах этого ребра, или не менять ни на одной
• для выполнения условия руководства необходимо поменять оклад с бонусом ровно в одной из вершин этого ребра

Забудем про все ребра первого типа и про ориентированность ребер второго и третьего типа. После этого объединим вершины, достижимые друг из друга по ребрам второго типа. После этого задача о проверке того, можно ли выполнить требование руководства, сводится к проверке того, можно ли раскрасить получившийся граф в два цвета, решающейся обходом в глубину.

Для получения минимального количества вершин, в которых нужно поменять местами оклад с бонусом, модифицируем этот поиск в глубину. После обхода и раскраски в два цвета очередной компоненты связности, посчитаем количество вершин (исходного графа, до объединения по ребрам второго типа), раскрашенных в тот и в другой цвет, и, при необходимости, инвертируем раскраску.

Задача F. Робот.

Идея: Борис Минаев.
Реализация: Борис Минаев, Артем Васильев
Разбор: Борис Минаев, Артем Васильев

В задаче требуется посчитать количество различных путей из одной клетки поля в другую за определенное количество шагов. При этом робот, который совершает действия, не может посетить конечную клетку раньше чем в последний ход. Также робот может ходить только по одной четверти бесконечной плоскости.

Для начала найдем количество способов добраться из одной клетки в другую без условия, что нельзя посещать конечную клетку раньше последнего хода. Такую задачу можно решать независимо по координатам, а потом перебрать, сколько ходов было совершено по одной координате, а сколько по другой. Как решать задачу в одномерном случае? Пусть изначально робот имеет координату x₁, а в конце должен иметь координату x₂. Пусть a=|x₂-x₁|, а всего было совершено t ходов. Тогда количество различных способов будет равно количеству сочетаний из t по (t-a)/2 (при этом t-a должно быть неотрицательным и четным). Однако нужно учесть, что робот может иметь только положительную координату в процессе путешествия. Для этого необходимо просто вычесть из полученного результата количество способов добраться из клетки -x₁ в x₂. Это справедливо, так как между путями из x₁, которые нарушают требование положительности координаты, а также всеми путями из -x₁ можно показать взаимно однозначное соответствие. Соответствующие друг другу пути будут иметь зеркальные первые части (до момента входа в клетку 0) и общие вторые части.

Вернемся к рассмотрению двумерной задачи. Пусть мы уже посчитали количество способов добраться по каждой координате от одной клетки до другой (для каждой фиксированной длины путешествия). Чтобы посчитать аналогичные значения для двумерной задачи, необходимо перебрать количество времени, которое потрачено на каждую координату, а потом перемножить соответствующие значения в уже посчитанных массивах, а также умножить на количество различных способов выбрать какие именно ходы будут соответствовать каким координатам. Чтобы посчитать эти значения быстро, можно воспользоваться преобразованием Фурье. Чтобы свести задачу к перемножению полиномов, необходимо избавиться от присутствия в формуле количества сочетаний. Для этого распишем его через факториалы. Сгруппировав слагаемые, получим, что можно i-е элементы исходных массивов поделить на i!, перемножить получившиеся полиномы, а потом значение в i-м разряде умножить на i! В задаче модуль, по которому необходимо выполнять все операции, был подобран таким образом, что по нему можно выполнять быстрое преобразование Фурье.

Теперь рассмотрим, как учесть то, что робот не может заходить в конечную клетку до последнего хода. Будем считать ответ с помощью динамического программирования. Пусть уже посчитано количество способов дойти до клетки за меньше чем t ходов. Чтобы посчитать это значения для t ходов, рассмотрим общее количество способов сделать это за t ходов и вычтем из него все способы, которые заходят в конечную клетку до хода t. Для этого переберем номер первого хода, в который робот посетит конечную клетку и умножим соответствующее ему количество способов на количество способов выйти из клетки (x₂, y₂) и вернуться в нее за оставшиеся время. При этом, робот может сколько угодно раз посещать конечную клетку (во второй части).

Заметим, что изложенное решение работает пока за t². Для более быстрого решения следует рассуждать в терминах производящих функций. Обозначим f(x) = f₀ x⁰ + f₁ x¹ + ... + f_t x^t + ..., где f_i — ответ не задачу. Аналогично определим count(x) — производящая функция для количества путей, без учета условия первого захода в конечную клетку на последнем ходу, cycle(x) — производящая функция для количества путей из конечной клетки в саму себя. Из рекуррентных соотношения для f_i, можно вывести соотношение на производящие функции: f(x) = count(x) — f(x) cycle(x), откуда f(x) = count(x) / (cycle(x) + 1) = count(x) (cycle(x) + 1)^-1. Для вычисления f необходимо посчитать первые t + 1 членов дроби в правой части. Это можно сделать, вычислив обратный к cycle(x) + 1 многочлен по модулю x^t+1, и перемножив count(x) с результатом. Взятие обратного многочлена по модулю x^t+1 можно выполнить за время O(t log t) с использованием быстрого преобразования Фурье. Итоговое время работы: O(t log t).

Всем привет!

Итак, четыре квалификации позади и приближается основное событие отборочного цикла Russian Code Cup 2014 — отборочный раунд. 802 участника сразятся за право войти в 50 лучших, которые будут приглашены в Москву в начале октября для участия в финальном раунде RCC-2014.

Отборочный раунд начнется в 14-00 по московскому времени в воскресенье, 8 июня, и продлится 3 часа.

Раунд завершен, поздравляем финалистов!

Задача А. Соцопрос.

Идея: Андрей Станкевич.
Реализация: Николай Ведерников.
Разбор: Николай Ведерников.

В задаче требуется найти минимальное и макимальное возможное количество участников, которые решат задачу. Если всего участников n, умеют решать задачу a, а задача противна b участникам.

Так как по условию задачи задачу решат только те, кому она не противна и умеют решать, то максимум, кто попытается решить задачу будет n−b. То есть если среди всех кто попытается решить задачу, будут те кто умеет, то это будет максимум кто решит, а это min(a, n−b).

Минимум же достигается, если все кому противна задача, будут уметь решать задачу, тогда ответ max(0, a−b)

Задача B. Сто.

Идея: Виталий Аксёнов.
Реализация: Павел Кротков.
Разбор: Павел Кротков.

Решением задачи является программа, аккуратно рассматривающая несколько несложных случаев. Самым простым случаем является ситуация, когда количество цифр в числе x равно k+1. В этом случае необходимо вывести −1, если число не содержит ни одного нуля, и ноль — если хотя бы один ноль в числе присутствует.

Если же количество чисел в числе x превышает k хотя бы на три, эту ситуацию необходимо обрабатывать более аккуратно. Найдем в числе второй ноль с конца. Убедимся, что за ним стоит не более, чем k+1 цифра. Вычеркнем из числа все ненулевые цифры, стоящие за вторым с конца нулем, а также вычеркнем необходимое количество цифр, стоящих сразу перед вторым с конца нулем. Заметим, что первая цифра никогда не вычеркивается, а значит, в итоговом числе не будет ведущих нулей.

Важно было не забыть о том, что операция вычеркивания цифры не должна выполняться за длину числа — решения с такой ошибкой получили превышение предела времени на третьем тесте.

Задача C. Поход в гости.

Идея: Георгий Корнеев.
Реализация: Борис Минаев.
Разбор: Борис Минаев.

Чтобы решить поставленную задачу необходимо аккуратно проэмулировать процесс, который описан в условии. При реализации удобно использовать встроенные средства для поддержания очереди. В самих очередях можно хранить, например, номер человека, который купил соответствующий подарок. Тогда очередной поход в гости происходит следующим образом. Возьмем элемент из очереди, которая соответствует человеку, идущему в гости. Если его очередь пуста, то будем считать, что из очереди был взят элемент, который соответствует этому человеку. После этого добавим данный элемент в очередь, которая соответствует человеку, к которому пришли в гости. Если значение добавленного элемента равно номеру очереди, в которую его добавили, необходимо вывести YES, иначе NO.

Задача D. СНМ.

Идея: Артем Васильев
Реализация: Артем Васильев
Разбор: Артем Васильев

В задаче была описана реализация системы непересекающихся множеств с ранговой эвристикой, но без эвристики сжатия путей. Будем решать задачу для каждого корневого дерева независимо, также следует рассмотреть случай наличия циклов.

Хоть массив rank и не задавался во входных данных, легко понять, что без сжатия путей, rank_i это высота поддерева с вершиной i в корне. Также отметим, алгоритм устроен так, что rank_i каждый раз увеличивается не более, чем на единицу, а после того, как вершина подвешивается к другой, ее parent и rank не изменяются, поэтому можно строить от листьев к корню.

Рассмотрим поддерево с корнем в вершине u. Если rank_u = r, то у вершины u должны существовать дети с рангом 0, 1, ..., r-1. Легко показать, что это условие является также достаточным: если провести операции union в порядке увеличения ранга сына, все операции пройдут корректно.

Отсюда следует решение для одного дерева:

• Рекурсивно построим решение для всех детей корня дерева.
• Проверим, что для всех h от 0 до rank_root — 1 существует сын с рангом h.
• Проделаем операции union(root, child_i) в порядке увеличения ранга child_i.

Время работы решения — O(n log (n)).

Задача E. Нанороботы.

Идея: Виталий Аксёнов.
Реализация: Андрей Комаров.
Разбор: Андрей Комаров.

В задаче требуется за минимальное число действий перемещения или разбиения на две части перевести всех нанороботов из левого верхнего угла в правый нижний.

Будем решать эту задачу при помощи динамического программирования. Обозначим за dp[w][x][y] минимальное число шагов, за которое можно довести робота массой w из клетки (x, y) до финальной клетки (n, m). Начальные значения dp[w][n][m] = 0 говорят о том, что из целевой клетки идти никуда не надо. После того, как dp будет посчитано, ответ будет содержаться в ячейке dp[w][1][1].

Научимся считать dp. Чтобы посчитать dp[w][i][j], сделаем одно из двух:

• Дойдём до финиша, не разбивая робота на части. Для этого, с помощью обхода в глубину, найдём кратчайший путь до финиша по выдерживающим клеткам.
• Либо, дойдём до какой-то клетки, разобъёмся на две части и дойдём ими оттуда.

Всем привет!

Все помнят, что исходно в RCC-2014 планировалось только 3 квалификационных раунда, но из-за ряда технических трудностей при проведении первой квалификации было решено провести четвертый раунд.

Поэтому в ближайшее воскресенье, 1 июня 2014 года, в 13-00 по московскому времени, состоится четвертый квалификационный раунд Russian Code Cup 2014.

Зарегистрироваться и участвовать можно на сайте http://russiancodecup.ru

Участвовать могут все, кроме тех участников, которые уже квалифицировались в первом, втором или третьем раундах.

200 лучших проходят в отборочный раунд, а остальным мы желаем удачи на других соревнованиях этого сезона и ждем на Russian Code Cup в следующем году.

Тем же, кто уже прошел в отборочный раунд, не стоит расслабляться, ведь он совсем скоро, 8 июня.

Раунд завершен. Поздравляю всех квалифицировавшихся!

Задача А. Треугольники.

Идея: Андрей Станкевич.
Реализация: Анна Малова.
Разбор: Анна Малова.

В задаче требуется определить количество треугольников каждого типа, которые можно составить из четырех отрезков.

Переберем все возможные тройки отрезков. Из трех отрезков можно составить треугольник, если выполнено неравенство треугольника, то есть сумма любых двух сторон строго больше длины третьей стороны.

Рассмотрим отрезки a, b, c в порядке возрастания длины, тогда если выполнено равенство c² = a² + b², то треугольник является прямоугольным, если c² < a² + b² остроугольным, и если c² > a² + b²— тупоугольным

Задача B. Оригами.

В задаче требуется проверить существует ли в прямоугольнике a на b подпрямоугольник площадью S, у которого стороны параллельны исходным.

Для этого переберём все такие x — делители числа S, и проверим, что x ≤ a и S ⁄ x ≤ b. Если существует хотя бы одна такая пара x и S ⁄ x, удолетворяющим ограничениям, то решение существует.

Время работы на один тестовый случай O(sqrt(S)).

Задача C. Митя и граф.

Идея: Жюри.
Реализация: Виталик Аксёнов.
Разбор: Виталик Аксёнов.

Первое наблюдение заключается в следующем: граф должен быть рёберным кактусом. Если он не получился таковым, то обязательно найдётся чётный цикл. Раз это кактус, то количество циклов равно m — (n — 1). А так как каждый цикл содержит в себе минимум 3 вершины, то 3·(m-(n — 1)) ≤ m. Отсюда получаем, что максимальное число рёбер равно 3·(n — 1) / 2.

При нечётных n, это мельница, то есть набор циклов длины 3, пересекающихся по 1 вершине, а при чётных n почти тоже самое, но еще одна висячая вершина соединена с любой другой ребром.

Задача D. Призы.

Идея: Виталик Аксёнов.
Реализация: Виталик Аксёнов.
Разбор: Виталик Аксёнов.

Мы знаем, что количества конфет, выданные участникам, должны убывать в зависимости от номера группы. Несложно убедиться, что любое удовлетворяющее разбиение конфет можно представить следующим способом:

• В начале, в первой группе дети получают n конфет, во второй — n-1 конфет, ..., в последней — 1 конфету.
• Далее мы можем прибавлять по одной конфете всем детям на префиксе групп. Это значит, что мы можем выбрать число p и увеличить a_i на единицу для любого i ≤ p.

Так как мы выбрали изначальное распределение, то из общего числа конфет можно сразу вычесть n·a₁+...+1·a_n. Несложно заметить, что операция распределения вычитает b_p = a₁+...+a_p. Итого, нам надо проверить, можем ли мы представить d в виде какой-то суммы b₁, ..., b_n, а это стандартная задача о рюкзаке.

Время работы O(nd).

Задача Е. Криптостойкие ключи

Идея: Виталий Демьянюк.
Реализация: Виталий Демьянюк.
Разбор: Виталий Демьянюк.

Дано множество чисел a₁, a₂, ..., a_n. Его замкнули относительно операций НОД и НОК. Требуется выяснить, принадлежит ли заданное число v замкнутому множеству S.

Представим v в виде p₁^q₁p₂^q₂... p_k^q_k, q _i > 0 , где p₁, p₂, ..., p_k — простые числа. Чтобы v принадлежало S необходимо чтобы для каждого i, 1 ≤  i ≤  k существовало j, 1 ≤  j ≤  n, такое что p_i^q_i ∣a_j и p_i^q_i+1 ∤a_j . Этот факт следует из того, что мы можем любое число представить в виде НОК(НОД(...), НОД(...), ..., НОД(...)), так как min(a, max(b, c)) = max(min(a, b), min(a, c)) и max(a, min(b, c)) = min(max(a, b), max(a, c)). Положим c_i равным наибольшему общему делителю чисел a_j, таких что p_i^q_i ∣a_j . Если все c_i делят v, то v принадлежит S. Оно может быть получено как наименьшее общее кратное всех c_i. В противном случае v не принадлежит S(это следует из свойств операций НОД и НОК).

Время работы O(nk + sqrt(v) ), где k — количество простых делителей числа v.

Всем привет!

В ближайшую субботу, 24 мая 2014 года, в 19-00 по московскому времени, состоится третий квалификационный раунд Russian Code Cup 2014.

Зарегистрироваться и участвовать можно на сайте http://russiancodecup.ru

Участвовать могут все, кроме 401 участника, которые уже квалифицировались в первом и втором раундах.

200 лучших проходят в отборочный раунд, а остальные смогут попробовать свои силы в четвертом квалификационном раунде 1 июня.

И немного приятных новостей: мы обновили версии компиляторов почти всех языков, добавили возможность отправлять на C++11 под GNU C++ (а Visual C++ 2013 и так поддерживает C++11) и добавили Java 8 (Java 7 тоже пока остается). Актуальные версии компиляторов и строки компиляции на странице с правилами чемпионата http://www.russiancodecup.ru/rules

Всем удачи!

[UPD] Всем спасибо за участие, раунд завершен. У нас снова 201 прошедший, поздравляем! Разбор будет опубликован в ближайшее время.

Всем привет!

В ближайшее воскресенье, 18 мая 2014 года, в 14-00 по московскому времени, состоится второй квалификационный раунд Russian Code Cup 2014.

Зарегистрироваться и участвовать можно на сайте http://russiancodecup.ru

Участвовать могут все, кроме 200 лучших (на самом деле 201, поскольку 200-е место было поделено) в первом квалификационном раунде.

200 лучших проходят в отборочный раунд, а остальные смогут попробовать свои силы в третьем и четвертом квалификационных раундах 24 мая и 1 июня.

Всем удачи!

Как заметили все, кто пытался принять участие в первой квалификации Russian Code Cup 2014, на протяжении всего раунда наблюдались технические проблемы с сервером, страницы с задачами и результатами были недоступны или доступны с большой задержкой.

Вне всякого сомнения, этот раунд не соответствует стандартам качества для нормального раунда, и его результаты не являются полностью достоверными. Было бы разумно сделать этот раунд "нерейтинговым" и провести вместо него новый квалификационный раунд.

С другой стороны, многие участники потратили время и силы на то, чтобы все же попытаться принять участие в раунде и порешать задачи, и нам хотелось бы их поощрить. Поэтому мы приняли следующее решение.

1) Несмотря на существенные проблемы во время раунда, чтобы поощрить тех участников, которые несмотря ни на что приняли в нем участие, 200 лучших из этого раунда проходят в отборочный раунд и получат футболку.

2) В воскресенье, 1 июня 2014 года в 13-00 будет проведен еще один, четвертый квалификационный раунд. 200 лучших участников четвертого раунда также выйдут в отборочный раунд и получат футболку, таким образом в отборочном раунде примут участие 800 участников, а не 600, как было исходно заявлено.

Мы понимаем, что решение спорное и в нем есть свои минусы, но надеемся на ваше понимание. Со своей стороны мы предпримем все возможные усилия, чтобы дальшнейшие раунды прошли без накладок и 50 сильнейших вышли в финал и сразились за звание чемпиона Russian Code Cup 2014.

Всем привет!

Напоминаю, что в субботу, 19 апреля 2014 года, в 12-00 по московскому времени, состоится первый квалификационный раунд Russian Code Cup 2014.

Зарегистрироваться и участвовать можно на сайте http://russiancodecup.ru

200 лучших проходят в отборочный раунд, а остальные смогут попробовать свои силы во втором и третьем квалификационных раундах 18 и 24 мая.

Всем удачи!

UPD: Принятое решение по итогам раунда

Тесты к прошедшему раунду: скачать тесты

417A - Отбор. Автор и реализация Aksenov239.

Сначала нужно заметить, что если k больше либо равно, чем n·m, то ответ — 0. Нам осталось набрать n·m - k человек. Есть три способа их набрать:

• Взять раунды только первого типа: .
• Взять чуть раундов второго типа до числа, делящегося на n: .
• Взять только раунды второго типа: d(n·m - k).

Также в данной задаче можно было написать переборное решение — сколько мы берём раундов первого типа, и сколько раундов второго.

Код: 6396283

417B - Сбой. Автор и реализация Aksenov239.

Заведём массив a на 10⁵ элементов, изначально заполненный  - 1, и в ячейке с номером k будем хранить максимальный номер посылки k-го участника, который сейчас есть. Будем обрабатывать посылки последовательно. Пусть обрабатывается посылка x k. Если a[k] < x - 1, то очевидно, что ответ NO, иначе обновляем массив — a[k] = max(a[k], x).

Код: 6396297

418A - Футбол. Автор и реализация Aksenov239.

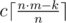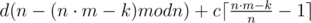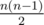Представим турнир себе как граф. Из каждой вершины ровно k выходящих рёбер. Тогда всего nk рёбер. В полном графе максимум рёбер, поэтому если n < 2k + 1, тогда ответ  - 1. Иначе, соединим i-ую вершину с i + 1, ..., i + k, зациклим если нужно.

Код: 6396331

418B - Хитрый Гена. Автор и реализация Aksenov239.

Давайте отсортируем друзей по возрастанию требуемого количества мониторов. Будем считать динамику на масках — какое минимальное число денег нужно заплатить, чтобы решить такие-то задачи, если мы взяли первых i друзей. Тогда ответ надо сравнить с ответом для i первых друзей плюс количество мониторов, которое требует i-ый друг. Не трудно заметить, что если брать друзей последовательно, то пересчитывать динамику можно как рюкзак. Время работы данного алгоритма O(nlog(n) + n2^m).

Код pashka: 6396347

418C - Квадратная таблица. Автор и реализация Aksenov239.

Давайте для любого n построим массив длины n, что сумма квадратов чисел на нём является квадратом:

• Если n = 1, то берём [1].
• Если n = 2, то берём [3, 4].
• Если n чётно, то берём .
• Если n нечётно, то берём .

Нам дано 2 числа n и m. Пусть массив a соответствует числу n, а b соответствует числу m.

Тогда итоговый массив c построим следующим способом — c_ij = a_i·b_j.

Код: 6396358

418D - Большие проблемы организаторов. Автор chavit, реализация Aksenov239.

В данной задаче есть два решения.

Первое. Подвесим за какую-нибудь вершину. Предподсчитаем для каждой, 3 самые удалённые вершины в её поддереве, а также для каждой вершины её глубину. Также предподсчитаем массивы для двоичного подъёма. Для каждой вершины i и степени двойки 2^j предподсчитаем следующие массивы — p[i][j], up[i][j] и down[i][j]. p[i][j] — это предок вершины i на расстоянии 2^j. В up[i][j] будет храниться наидлиннейший путь из i, до вершин, которые находятся в поддереве вершин, которые находятся на пути между i и p[i][j]. down[i][j] отличается от up[i][j], что хранит путь из вершины p[i][j].

Теперь осталось дело за малым. Нам приходит запрос u v, мы ищем его наименьшего общего предка — w. Осталось найти вершину hu, которая будет находиться на середине это пути. Обрезать дерево по этой вершине, и посчитать длиннейшее расстояние от вершины u в её дереве и длиннейшее расстояние от вершины v в её дереве. Представляя на дереве это, если мы не будем удалять, то можно воспользовавшись нашими предподсчитанными массивами аккуратно пересчитать значение длиннейшего пути.

Решение за O(nlog(n)).

Код: 6396376

Второе. Вкратце. Найдём диаметр этого дерева. Предподсчитаем там ответ на префиксе для каждой вершины. Тогда при ответе на запрос — мы находим, когда путь вливается диаметр. На это отрезке находим среднюю вершину, а далее отвечаем на запрос на префиксе или суффиксе.

Код cerealguy: 6396390

418E - Хитрый пароль. Авторы enot110, Aksenov239, реализация Aksenov239

Ключевая теоретическая идея данной задачи заключается в том, что 2 строка совпадает с 4, 3 с 5 и т. д. Поэтому нам нужно уметь менять что-то только на первых трёх строках.

Теперь дело остаётся за практической частью. В первую очередь сожмём все значения, чтобы они не превосходили 10⁵. Разобьём массив на отрезки длиной LEN. На каждом отрезке будем считать следующее — для каждого значения будем хранить сколько раз он встречался на префиксе cnt, а так же дерево Фенвика, в котором в ячейке f[k] будет храниться количество чисел на данном префиксе, встречающихся ровно k раз. Несложно заметить, что в первом массиве хранится ответ на запросы ко второй строке, а чтобы получить ответ для третьей строки, нужно посчитать f[cnt[k]... 10⁵]. Понятно так же, как делать пересчёт данной динамики.

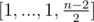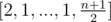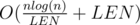Итого, получаем время на запрос за . Если мы возьмём 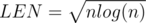, то время ответа на запрос составит .

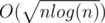Код: 6396412

Очередной сезон крупнейшей российской олимпиады Russian Code Cup стартует в субботу. Впереди новые интересные и нетривиальные задания, бескомпромиссная борьба и самые крутые призы.

Но мы подготовили вам еще один сюрприз: 17 апреля у каждого из вас есть возможность оценить свои силы. В 19:30 по московскому времени на площадке http://codeforces.ru состоится тренировочный раунд олимпиады со свежей порцией задач от создателей RCC.

RCC 2014 Warmup – это тест, который даст возможность попробовать свои силы и понять, к чему готовиться в раундах чемпионата. А для «бывалых» участников это идеальная возможность потренироваться и разогреться перед первыми сражениями RCC 2014!

Автором большинства задач этого раунда является Aksenov239 — постоянный автор задач RCC. Конечно же ему помогали и другие члены жюри RCC-2014. Раунд пройдет как в div-1, так и в div-2, так что все найдут себе задачи по силам.

Ждем вас в четверг в 19:30 на площадке http://codeforces.ru

UPD: Итак, разбалловка раунда: Div1: 500-1000-1500-2500-2500, Div2: 500-1000-1500-2000-2500. Всем удачи!

Определены даты проведения крупнейшей в России ежегодной олимпиады по спортивному программированию Russian Code Cup 2014. В этом году программисты сразятся за звание лучшего (и за главный приз – 10 тысяч долларов США) в четвертый раз. Регистрация на чемпионат уже идет, а первый тур состоится уже в эту субботу, 19 апреля!

Russian Code Cup – это возможность для русскоязычных программистов со всего мира проверить свои силы и продемонстрировать мастерство, решая оригинальные задачи различной сложности, а также заявить о себе экспертному IT-сообществу.

Олимпиада проходит в три этапа: квалификационные раунды, отборочный тур и финал, на каждом из которых участникам олимпиады предлагается от четырех до восьми разноплановых задач. Задания и техническую часть соревнования обеспечивают специалисты Mail.Ru Group и эксперты НИУ ИТМО – соорганизатора Russian Code Cup.

На первых двух этапах программисты соревнуются онлайн на сайте Russian Code Cup. Первый квалификационный раунд состоится 19 апреля в 12:00, второй – 18 мая в 19:00, третий – 24 мая в 14:00. Причем программисты, не прошедшие квалификацию с первого раза, могут попробовать свои силы в следующих раундах.

В отборочный тур, назначенный на 14:00 8 июня, пройдут 200 лучших участников из каждого квалификационного раунда. А 50 программистов, преодолевших «сито» отбора, померятся силами в финале, который состоится в октябре 2014 года в офисе Mail.Ru Group.

Победитель Russian Code Cup получит главный приз – 10 тысяч долларов США; участник, занявший второе место, — 5 тысяч долларов США; приз за третье место – 3 тысячи долларов США. Кроме того, ценные призы достанутся всем участникам, дошедшим до финала.

Для того чтобы принять участие в Russian Code Cup, нужно зарегистрироваться на сайте http://russiancodecup.ru/ (регистрация будет открыта до начала третьего квалификационного раунда).

Подробнее о чемпионате, правилах и призах и читайте на сайте http://russiancodecup.ru, по всем вопросам обращайтесь на russiancodecup@corp.mail.ru