Hello everyone,
finding the diameter is one of the most frequent ways to solve problems about trees. In this tutorial we will see how to find a diameter and some of its properties, and we will use them to solve some problems of increasing difficulty.
The first part of the tutorial is quite basic, so feel free to skip it and jump to the problems if you already know the concepts.
Target: rating $$$[1400, 2100]$$$ on CF
Prerequisites: basic graph theory, greedy
The diameter
Given an unweighted tree, let's define $$$\text{dist}(a, b) =$$$ the number of edges in the simple path $$$a \rightarrow b$$$.
A diameter of the tree is a simple path $$$a \rightarrow b$$$ that maximizes $$$\text{dist}(a, b)$$$ over all pairs of nodes. If there are multiple diameters, let's pick any of them.
The same definition is valid for a weighted tree with nonnegative weights (with $$$\text{dist}(a, b) =$$$ the sum of the weights of the edges in the simple path $$$a \rightarrow b$$$).
Finding a diameter
Given a tree with $$$n$$$ nodes are multiple ways to find a diameter. Here is one of the simplest ways:
Run a DFS from any node $$$p$$$. Let $$$a$$$ be a node whose distance from node $$$p$$$ is maximized. Run another DFS from node $$$a$$$. Let $$$b$$$ be a node whose distance from node $$$a$$$ is maximized. $$$a \rightarrow b$$$ is a diameter.
Tree = edges of a diameter + forest
Before proving the previous algorithm, let's analyze the structure of the tree (we will mention the diameter, but we will not use the fact that $$$a \rightarrow b$$$ is actually a diameter before proving it).
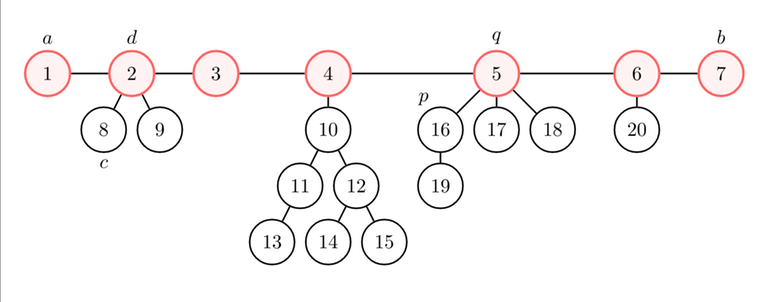
We started a DFS from node $$$p = 16$$$, and we got that node $$$a = 1$$$ is the farthest from $$$p$$$, and node $$$b = 7$$$ is the farthest from $$$a$$$.
Let's represent the diameter on a line. If you remove the edges of the diameter, you get a forest (i.e., several trees). Let's root each tree at the node in the diameter. What's the height (i.e., the maximum distance from the root to any node) of each component?
Let $$$q$$$ be the root of the component of $$$p$$$. Let's consider any component whose root $$$d$$$ is between $$$a$$$ (included) and $$$q$$$ (excluded), and one of its nodes $$$c$$$.
We get
$$$\text{dist}(p, a) \geq \text{dist}(p, c) \implies \text{dist}(p, a) - \text{dist}(p, d) \geq \text{dist}(p, c) - \text{dist}(p, d) \implies \text{dist}(a, d) \geq \text{dist}(c, d)$$$.
In other words, the height of each component with root in the left half of the diameter (i.e., $$$\text{dist}(a, d) < \text{dist}(d, b)$$$) is at most the distance of the root of the component from the left end of the diameter.
You can prove the same statement for the right half of the diameter (i.e., $$$\text{dist}(a, d) \geq \text{dist}(d, b)$$$), using that $$$b$$$ is the farthest node from $$$a$$$.
Farthest node for each node
For each node $$$i$$$, let's find a node $$$j$$$ such that $$$\text{dist}(i, j)$$$ is maximum.
Claim: $$$j = a$$$ or $$$j = b$$$ always works.
Proof:
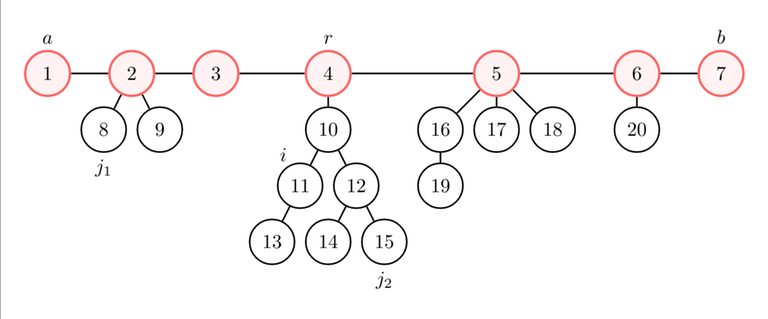
- If $$$j = j_1$$$ works ($$$j_1$$$ is not in the same component of $$$i$$$; let's assume without loss of generality that $$$j_1$$$ is closer to $$$a$$$ than to $$$b$$$), $$$\text{dist}(i, j_1) = \text{dist}(i, r) + \text{dist}(r, j_1) \leq \text{dist}(i, r) + \text{dist}(r, a) = \text{dist}(i, a)$$$. Then, $$$j = a$$$ also works.
- If $$$j = j_2$$$ works ($$$j_2$$$ is in the same component of $$$i$$$), $$$\text{dist}(i, j_1) \leq \text{dist}(i, r) + \text{dist}(r, j_1) \leq \text{dist}(i, r) + \text{dist}(r, a) = \text{dist}(i, a)$$$. Then, $$$j = a$$$ also works.
Proof that $$$a \rightarrow b$$$ is a diameter
Now we can finish the proof.
Suppose that $$$u \rightarrow v$$$ is a diameter. We have either $$$\text{dist}(u, a) \geq \text{dist}(u, v)$$$ or $$$\text{dist}(u, b) \geq \text{dist}(u, v)$$$ (see "Farthest node for each node").
Let's assume without loss of generality that $$$\text{dist}(u, b) \geq \text{dist}(u, v)$$$. We get $$$\text{dist}(a, b) \geq \text{dist}(u, b) \geq \text{dist}(u, v)$$$, so $$$a \rightarrow b$$$ is a diameter.
Observations
The algorithm also works in a weighted tree with positive edges (we've never used that the weights are $$$1$$$).
However, it doesn't work on general graphs (discussion).
How to use the diameter
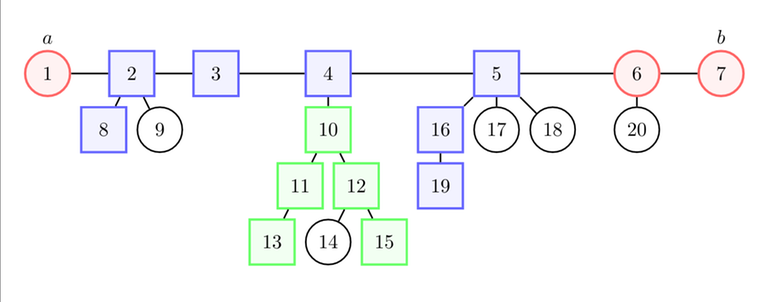
Most of the times, spamming "the farthest node from each node is one end of the diameter" and "the height of each component is smaller than the distance to the closest end of the diameter" is enough to reduce the problem to something simpler.
You may need to consider any path of the tree. Find a diameter $$$a \rightarrow b$$$. There are two cases: the path intersects (blue) or doesn't intersect (green) the diameter.
Then, you may wonder how to make the path longer / "more optimal" / etc. according to the statement. For example, you may need to use $$$\text{dist}(7, 5) \geq \text{dist}(5, 19)$$$ to show that $$$8 \rightarrow 7$$$ is "more optimal" than $$$8 \rightarrow 19$$$.
1004E - Sonya and Ice Cream (rating: 2400)
633F - The Chocolate Spree (rating: 2600)
arc088_e (rating: 2231)
arc097_e (rating: 2247)
Other problems
102694B - Dynamic Diameter
abc221_f
Conclusions
We've seen that a lot of problems where you have to swap adjacent elements can be tackled with greedy observations, such as looking at the optimal relative positions of the values in the final array; then, a lot of these problems can be reduced to "find the number of inversions" or similar.
Of course, suggestions/corrections are welcome. In particular, please share in the comments other problems where you have to swap adjacent elements.
I hope you enjoyed the blog!






