Hi everyone!
The usage of generating functions is quite common in competitive programming these days. But it seems to happen so, that they're mostly presented as a way to simplify formal manipulation with polynomial coefficients, rather than something meaningful. But there actually is a meaning to all of this, and today I'm going to shed a light on it.
Alongside the blog post we'll uncover the combinatorial meaning of
- The addition $$$F(x)+G(x)$$$,
- The multiplication $$$F(x)G(x)$$$,
- The exponent $$$\exp F(x)$$$,
- The logarithm $$$\log F(x)$$$,
- The sum of the infinite geometric progression $$$\frac{1}{1-F(x)}=1+F(x)+F^2(x)+\dots$$$,
- The general composition $$$F(G(x))$$$
for the generating functions $$$F(x)$$$ and $$$G(x)$$$ and the underlying structures they represent.
Prerequisites
- Basic notion of set theory (cardinality of sets, mappings, bijections, cartesian product, disjoint union, etc);
- Polynomials and formal power series (representation, convolution formula, power series definitions of $$$\exp$$$ and $$$\log$$$);
- Elementary combinatorics (combinations, partitions, etc).
Although combinatorial species are defined with category theory concepts, I will try to avoid them for simplicity. However, knowledge of some category theory concepts would greatly simplify the reading experience.
Some of definitions use pretty dense mathematical notation, I will follow up with informal explanation right away when it is the case.
Commutative diagrams
I will also use commutative diagrams to illustrate complicated identities. You may use the explanation below as a reference.
Every diagram is also provided with a more verbose text description, so don't be afraid if the concept seems complicated.
Definitions
A mapping $$$F$$$ that maps elements of $$$A$$$ to elements of $$$B$$$ is denoted as $$$F : A \to B$$$.
Def. 1. The identity map $$$\operatorname{Id}_A : A \to A$$$ is defined as $$$\operatorname{Id}_A(a) = a$$$ for $$$a \in A$$$.
Def. 2. Let $$$F : A \to B$$$ and $$$G : B \to C$$$. Then the composition $$$G \circ F$$$ is defined as $$$(G \circ F)(a) = G(F(a))$$$ for $$$a \in A$$$.
In the definition below we use a notion of a class. Informally, it is a collection of sets joined by some property, which does not have to be a set of its own, but for which we may still consider some mappings (functions) on top of it. It is also possible to formalize the concept or to bypass the need for it to not be a set, see the comment below.
Alternatively, if you're really uncomfortable working with proper classes (which requires the addition of new axioms to the Zermelo-Fraenkel set theory), you may assume that the work is done in the set of hereditarily finite sets rather than the class of finite sets.
Def. 3. Let $$$U$$$ be a class of finite sets. A combinatorial species is a mapping $$$F : U \to U$$$ and a family of bijections $$$F_\sigma : F(A) \to F(B)$$$ defined for every bijection $$$\sigma : A \to B$$$ between $$$A,B \in U$$$ in such way that
- If $$$\sigma : A \to B$$$ and $$$\tau : B \to C$$$ are bijections, then $$$F_{\tau \circ \sigma} = F_\tau \circ F_\sigma$$$;
- For $$$B=A$$$ and $$$\operatorname{Id}_A : A \to B$$$ it holds that $$$F_{\operatorname{Id}_A} = \operatorname{Id}_{F(A)}$$$.
The elements of $$$F(A)$$$ are called the $$$F$$$-structures and the bijection $$$F_\sigma$$$ is called the transport of $$$\sigma$$$ along $$$F$$$-structures.
In category theory terms, a combinatorial species is a functor on the category of finite sets.
Informally, $$$F(A)$$$ is a set of combinatorial structures (graphs, trees, sequences, etc) that are defined by the species $$$F$$$ and labeled by the elemenets of $$$A$$$. The bijections $$$F_\sigma$$$ define the rules in which structures change after re-labeling. In this terms, the rules are read as
- Re-labeling from $$$A$$$ to $$$B$$$ using $$$\sigma$$$ and then from $$$B$$$ to $$$C$$$ using $$$\tau$$$ should be same as re-labeling directly from $$$A$$$ to $$$C$$$ using $$$\tau \circ \sigma$$$;
- Re-labeling from $$$A$$$ to $$$A$$$ using the identity map should not change $$$F(A)$$$.
For example, let $$$F$$$ be a species of labeled trees. Then, $$$F(A)$$$ should map $$$A$$$ to a set of all labeled trees that can be build on $$$|A|$$$ vertices, such that each vertex is labeled by an element from $$$A$$$. On the picture below, you see $$$F(A_2)$$$, $$$F(A_3)$$$ and $$$F(A_4)$$$:
Labeled trees on sets $$$A_2 = \{{\color{red} \bullet}, {\color{blue} \bullet}\}$$$, $$$A_3 = \{{\color{red} \bullet}, {\color{blue} \bullet}, {\color{green} \bullet}\}$$$ and $$$A_4 = \{{\color{red} \bullet}, {\color{blue} \bullet}, {\color{green} \bullet}, {\color{goldenrod} \bullet}\}$$$.
The image by Júlio Reis is distributed under CC BY-SA 3.0 license.
Correspondingly, if you were to change labels from $$$A_4 = \{{\color{red} \bullet}, {\color{blue} \bullet}, {\color{green} \bullet}, {\color{goldenrod} \bullet}\}$$$ to $$$X_4 = \{1,2,3,4\}$$$ with a mapping $$$\sigma : A_4 \to X_4$$$, the bijection $$$F_\sigma : F(A_4) \to F(X_4)$$$ would map each tree from $$$F(A_4)$$$ to $$$F(X_4)$$$ according to the way labels are changed from $$$A_4$$$ to $$$X_4$$$ by $$$\sigma$$$.
Further examples
- Set species is defined as $$$E(A) = \{A\}$$$, combinatorial structure is a set of $$$|A|$$$ elements labeled by $$$A$$$;
- $$$n$$$-set species is defined as $$$E_n(A)= \{A\}$$$ if $$$|A|=n$$$ and $$$E_n(A)=\varnothing$$$ otherwise;
- Singleton species $$$X$$$ is defined as $$$X(A)=E_1(A)$$$;
- Subset species is defined as $$$F(A) = 2^A$$$, combinatorial structure is a subset of $$$A$$$;
- Permutation species $$$S$$$ is defined as $$$S(A) = S_{A}$$$, combinatorial structures are permutations (bijections to itself) of $$$A$$$;
- Graph species is defined as $$$F(A) = \{(A, E) : E \subset A \times A\}$$$, combinatorial structures are graphs with $$$A$$$ as vertices;
- Cycle species $$$C$$$ corresponds to combinatorial structures being cycles of $$$|A|$$$ elements labeled by $$$A$$$;
- Partition species $$$\operatorname{Par}$$$ corresponds to combinatorial structures being partitions of $$$A$$$;
- Linear order species $$$L$$$ corresponds to combinatorial structures being ordered $$$|A|$$$-tuples of distinct elements from $$$A$$$.
Species isomorphism
Def. 4. Let $$$F$$$ and $$$G$$$ be two species. Species isomorphism $$$\alpha$$$ is a family of bijections $$$\alpha_A : F(A) \to G(A)$$$ for $$$A \in X$$$, such that for every bijection $$$\sigma : A \to B$$$, and every $$$f \in F(A)$$$ it holds that $$$G_\sigma(\alpha_A(f)) = \alpha_B(F_\sigma(f))$$$.
In category theory terms, the mapping $$$\alpha$$$ is a natural transformation.
Informally, $$$\alpha_A$$$ tells us how to transform any combinatorial structure of the species $$$F(A)$$$ into the one of $$$G(A)$$$, so that the transform is consistent with any re-labeling from $$$A$$$ to $$$B$$$.
Further on, when writing $$$F=G$$$ for species $$$F$$$ and $$$G$$$ we will mean that the species are isomorphic.
Examples
Let $$$X_n = \{1, 2, \dots, n\}$$$.
- Species of subsets is isomorphic to the species of ordered possibly empty partitions into two blocks.
- E.g. the subset $$$\{1, 3, 4\}$$$ of $$$X_5$$$ corresponds to the partition $$$(\{1,3,4\}, \{2, 5\})$$$.
- Species of permutations is isomorphic to the species of sets of cycles.
- E.g. the permutation $$$\sigma = \binom{1~2~3~4}{2~1~4~3}$$$ corresponds to the set of cycles $$$\{(1 \to 2), (3 \to 4)\}$$$.
Note that the species of linear orders $$$G$$$ (orderings of $$$A$$$) are not isomorphic to the species of permutations $$$F$$$, even though $$$|F(X_n)|=|G(X_n)|=n!$$$. Consider $$$F(X_2) = \left\{\binom{1~2}{1~2},\binom{1~2}{2~1}\right\}$$$ and $$$G(X_2) = \{(1,2), (2, 1)\}$$$. If we relabel with $$$\sigma(1)=2$$$ and $$$\sigma(2)=1$$$, elements of $$$F(X_2)$$$ will not change, while elements of $$$G(X_2)$$$ will get swapped. Hence, there is no $$$\alpha$$$ consistent with such $$$\sigma$$$.
Operations on species
The operations defined below are the core ones that are related to generating functions.
This section uses the concept of the disjoint union of two sets. For sets $$$A$$$ and $$$B$$$, their disjoint union $$$A \sqcup B$$$ is constructed in such way that every element that belongs to both $$$A$$$ and $$$B$$$ appears twice: once as an element of $$$A$$$ and once as an element of $$$B$$$. This is unlike the regular union in which elements from the intersection appear once. You can define the disjoint union formally as
where $$$\circ$$$ marks the elements from $$$A$$$ and $$$\bullet$$$ marks the elements from $$$B$$$.
The disjoint union of $$$A$$$ and $$$B$$$ is formed by the union of elements labeled by the set they came from.
The image by Kismalac is distributed under CC BY-SA 3.0 license.
Def. 5. The addition $$$F+G$$$ of species $$$F$$$ and $$$G$$$ is defined as their disjoint union:
Informally, $$$(F+G)$$$-structure is either an $$$F$$$-structure or a $$$G$$$-structure.
Def. 6. The cartesian product $$$F \times G$$$ of species $$$F$$$ and $$$G$$$ is defined as
Informally, $$$(F \times G)$$$-structure is a pair of an $$$F$$$-structure and a $$$G$$$-structure, both constructed on the set $$$A$$$.
Def. 7. The ordinary product $$$F \cdot G$$$ of species $$$F$$$ and $$$G$$$ is defined as
Informally, $$$(F \cdot G)$$$-structure on $$$A$$$ is a pair of an $$$F$$$-structure on $$$B$$$ and a $$$G$$$-structure on $$$C$$$ such that $$$(B, C)$$$ is an ordered partition of $$$A$$$.
$$$A$$$ is partitioned in $$$A = B \sqcup C$$$, then an $$$F$$$-structure is constructed on top of $$$B$$$ and a $$$G$$$-structure is constructed on top of $$$C$$$.
The image by Brent Yorgey is distributed under CC BY-SA 3.0 license.
Def. 8. Let $$$\pi$$$ be an unordered partition of $$$A$$$. The composition $$$F \circ G$$$ of species $$$F$$$ and $$$G$$$ is defined as
Here $$$\prod$$$ denotes the cartesian product over all elements of $$$\pi$$$.
Informally, $$$(F \circ G)$$$-structure on $$$A$$$ is an $$$F$$$-structure built on top of $$$G$$$-structures that are constructed on each element of the partition.
$$$A$$$ is partitioned by $$$\pi$$$, a $$$G$$$-structure is formed on top of each element of $$$\pi$$$, then an $$$F$$$-structure is formed on top of $$$\pi$$$.
The image by Brent Yorgey is distributed under CC BY-SA 3.0 license.
Examples
Species of sets and sequences as a sum of simpler species.
- The set species can be represented as a sum of all $$$n$$$-set species:
- The species $$$L_n$$$ of linear orders of $$$n$$$-sets is isomorphic to $$$X^n=E_1^n$$$ and
- The non-empty sets species $$$E^+$$$ is represented as
Neutral elements for operations.
- Empty species $$$0 = G$$$ such that $$$G(A)=\varnothing$$$ for any $$$A$$$ is the neutral element of the species addition. That is, $$$0 + G = G + 0 = G$$$.
- Empty set species $$$1 = E_0$$$ is the neutral element of the species ordinary product. That is, $$$1 \cdot F = F \cdot 1 = F$$$.
- Singleton species $$$X = E_1$$$ is the neutral element of the species composition. That is, $$$X \circ F = F \circ X = F$$$.
Species as compositions of simpler species.
- $$$E \circ G$$$ is a species of sets of $$$G$$$-structures, $$$E_n \circ G$$$ is a species of $$$n$$$-sets of $$$G$$$-structures;
- $$$S = E \circ C$$$: a species of permutations is isomorphic to the species of sets of cycles;
- $$$\operatorname{Par} = E \circ E^{+}$$$: a species of partitions is a species of sets of non-empty sets;
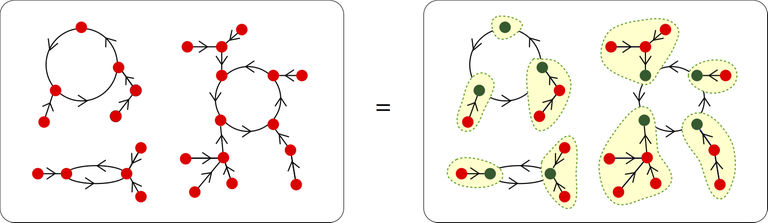
Function species is a set of cycles of rooted trees
An illustration from Combinatorial Species article by François Bergeron
- $$$f = S \circ T$$$: a species $$$f$$$ of functions from $$$A$$$ to $$$A$$$ can be represented as a permutation (set of cycles) of rooted tree species $$$T$$$.
Recursively defined species.
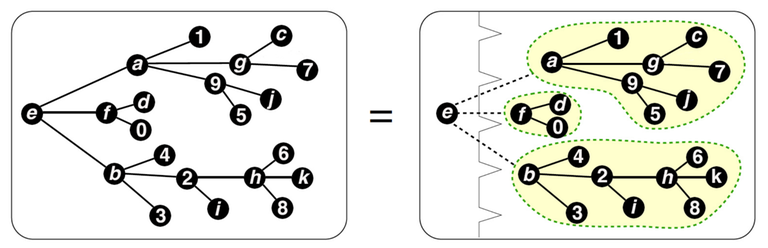
An ordered tree may be represented as a root, followed by a sequence of ordered trees.
An illustration from Binomial species and combinatorial exponentiation article by Gilbert Labelle.
A species $$$\triangle$$$ of ordered trees is described as a tree, in which the children of each node are ordered. In other words, ordered tree is a pair $$$(x, L)$$$, where $$$x$$$ is a node of the tree and $$$L$$$ is a possibly empty ordered tuple of its subtrees. Therefore, in terms of species operations,
where $$$X=E_1$$$ is a node of the tree and $$$1=E_0$$$ is the empty sequence.
In the picture above, the set $$$A=\{a,b,c,d,e,f,g,h,i,j,k, 0,1,2,3,4,5,6,7,8,9\}$$$ is first split in a pair
which corresponds to the ordinary product of singleton species and the sequence of ordered trees. The label $$$e$$$ from the first set is given to the root and the set of remaining labels then is given to the "list of trees". Then the later set is partitioned with
At last, another tree species is constructed on each set from $$$\pi$$$ and then the sequence species constructed on $$$\pi$$$ itself to make it ordered, which corresponds to the composition of the sequence species and ordered tree species.
Cardinalities of species operations
Note that the cardinality of $$$F(A)$$$ is determined by the cardinality of $$$A$$$ (otherwise $$$F_\sigma$$$ wouldn't be a bijection).
Let $$$f_i = |F(A)|$$$ for $$$|A|=i$$$ and $$$g_j = |G(A)|$$$ for $$$|A|=j$$$. What can we say about $$$|(F+G)(A)|$$$ and $$$|(F\cdot G)(A)$$$ for $$$|A|=k$$$?
- For disjoint union, the formula is simple:
- Correspondingly, for the cartesian product:
- For the ordinary product:
- And for the composition (assuming $$$g_0=0$$$):
In the last two formulas we have used the fact that there are $$$\binom{k}{i}$$$ ways to partition a set $$$A$$$ of size $$$k$$$ into sets $$$B$$$ and $$$C$$$ of sizes $$$i$$$ and $$$k-i$$$. Similarly for the composition, there are
ways to partition a set into $$$i$$$ sets of sizes $$$j_1, \dots, j_i$$$. The division by $$$i!$$$ here is needed to account for partitions being unordered, as every unordered partitions is counted for every permutation of $$$(j_1, \dots, j_i)$$$ and there are $$$i!$$$ such permutations.
Generating functions
The idea behind generating functions is to define a class of objects with operations of sum, product and composition that is consistent with a way these operations are defined above for species. The formulas above for the ordinary product and the composition could be rewritten in the following way:
- For $$$h_k = |(F \cdot G)(A)|$$$ with $$$|A|=k$$$:
- For $$$h_k = |(F \circ G)(A)|$$$ with $$$|A|=k$$$:
These formulas are consistent with the following definition:
Def. 9. The exponential generating function (EGF) of a species $$$F$$$ is defined as a formal power series
where $$$f_k = |F(X_k)|$$$ is the number of $$$F$$$-structures you could build on a set of $$$k$$$ elements.
With this definition, we can show that
- The addition of species yields the addition of the generating functions:
- The cartesian product of species yields something similar to the Hadamard product of the generating functions:
- The ordinary product of species yields the product of the generating functions:
- The composition of species yields the composition of the generating functions:
The last formula is only valid for $$$G(0)=g_0=0$$$, that is $$$G(\varnothing)=\varnothing$$$, as all sets in the partition are non-empty.
Examples
EGF of sets. The EGF of sets species is
The expression above provides the combinatorial meaning to $$$\exp F(x)$$$ and $$$\log F(x)$$$ operations on the generating functions. Specifically, $$$\exp F(x)$$$ is the generating function for the disjoint sets of $$$F$$$ structure, while $$$\log F(x)$$$ makes the inverse transform from disjoint sets of $$$G$$$ to $$$G$$$ itself. The result more commonly known as the exponential formula.
The EGF of $$$n$$$-sets species is $$$E_n(x)=\frac{x^n}{n!}$$$. In particular, the EGF of a singleton species is $$$X(x)=E_1(x) = x$$$.
EGF of permutations. The EGF of permutations species is
Permutations species is isomorphic to sets of cycles, that is $$$S = E \circ C$$$. It means that
where $$$C(x)$$$ is the generating function of cycles. Therefore,
Indeed, there are $$$(k-1)!$$$ ways to make a cycle out of $$$k$$$ distinct elements.
EGF of sequences. Species of linear orders is an ordered tuple of $$$k$$$ singletons for some $$$k$$$, hence
Another way to get it is to note that $$$L = E_0 + X \cdot L$$$, that is any sequence is either empty (corresponds to $$$E_0$$$) or can be represented as a pair of the first element (corresponds to $$$X$$$) and the sequence constructed from remaining elements (corresponds to $$$L$$$ in $$$X \cdot L$$$). This yields an equation $$$L(x) = 1+xL(x)$$$.
EGF of partitions. The partition is a set of non-empty sets: $$$\operatorname{Par} = E \circ E^+$$$. Therefore, the EGF of the partition species is
EGFs related to Catalan numbers. In the examples below we work with labeled versions of balanced bracket sequences and trees. Informally, it means that each vertex of the tree has a label (e.g. a number from $$$1$$$ to $$$n$$$) and each pair of brackets in the bracket sequence is also associated with some label.
Changing labels on the same tree/bracket sequence generally leads to a different object with the same underlying structure. For "unlabeled" case see the next section.
Balanced bracket sequence species $$$B$$$ is a (possibly empty) sequence (linear order) of balanced bracket sequences, each of them wrapped in a pair of brackets. The generating function for the balanced bracket sequence wrapped in a pair of brackets is $$$X \cdot B$$$ (as it can be represented as a pair of the outer brackets, perceived as a singleton, and the underlying sequence). Correspondingly, a sequence of wrapped bracket sequences is $$$L \circ (X \cdot B)$$$ and it has a generating function $$$L(xB(x))$$$. Therefore:
Solving the equation above for $$$B(x)$$$ yields $$$xB^2(x) - B(x) + 1 =0$$$, hence
which corresponds to the genfunc of the Catalan numbers.
Ordered tree species $$$\triangle$$$ adheres to the identity $$$\triangle = X \cdot (L \circ \triangle)$$$. Thus,
Solving the equation for $$$\triangle(x)$$$ yields $$$\triangle^2(x) - \triangle(x) + x = 0$$$, hence
which is also the generating function for the Catalan numbers.
Functions and rooted trees. Recall the species of functions $$$f$$$ and rooted trees $$$T$$$ that were introduced in the previous section. Counting rooted trees is not a trivial task, but we know that there are $$$n^n$$$ functions from a set of size $$$n$$$ onto itself. That means that
but on the other hand $$$f = S \circ T$$$, so
from which we get
Unlabeled species
The techniques and concepts developped above also can be used to deal with unlabeled objects.
Def. 10. Two structures $$$\alpha, \beta \in F(A)$$$ are equivalent if there is a bijection $$$\sigma: A \to A$$$ such that $$$F_\sigma(\alpha) = \beta$$$.
Informally, the structures are equivalent if one is obtainable from another via re-labeling to the same set $$$A$$$.
Def. 11. An unlabeled structure is an equivalence class on $$$F(A)$$$ under the equivalence relation defined above.
Informally, unlabeled structure is what we get if we "erase" labels in $$$F(A)$$$ (e.g. erase labels of vertices in graphs, etc).
On the left and on the right are equivalent trees. In the middle is the representation of their unlabeled structure.
Def. 12. The ordinary generating function (OGF) of a species $$$F$$$ is defined as a formal power series
where $$$\tilde f_k$$$ is the number of unlabeled $$$F$$$-structures on $$$X_k$$$.
One can prove that $$$\widetilde{(F \cdot G)}(x) = \widetilde F(x) \widetilde G(x)$$$ and $$$\widetilde{(F+G)}(x) = \widetilde F(x) + \widetilde G(x)$$$. The ordinary product formula stands, as you do not have to multiply by $$$\binom{k}{i}$$$ to account for the distribution of labels between the first and the second sets of the partition.
At the same time, $$$\widetilde{(F \circ G)}(x)$$$ generally can't be computed just from $$$\widetilde F(x)$$$ and $$$\widetilde G(x)$$$.
Examples
- The OGF of $$$L$$$ species is $$$\widetilde L(x) = \sum\limits_{k=0}^\infty x^k = \frac{1}{1-x}$$$, as all ordered $$$n$$$-tuples are equivalent under re-labeling.
- The OGF of $$$S$$$ species is $$$\widetilde S(x) = \prod\limits_{k=1}^\infty \frac{1}{1-x^k}$$$ is the generating function of partitions, as permutations are equivalent under re-labeling if and only if they have the same cycle type, and the number of distinct cycle types of permutations of size $$$n$$$ amounts for the number of partitions of $$$n$$$.
As you see, although $$$L(x)=S(x)$$$, at the same time $$$\widetilde L(x) \neq \widetilde S(x)$$$, which highlights the fact that $$$S$$$ and $$$L$$$ are not isomorphic species.
Exercises
Composition formula for sequences. Show that $$$\widetilde{(L \circ F)}(x) = \widetilde L(\widetilde F(x))=\frac{1}{1-\widetilde F(x)}$$$ for any species $$$F$$$.
Counter-example to general composition formula. Show that $$$\widetilde X(x) = x$$$, $$$\widetilde E(x) = \frac{1}{1-x}$$$, but $$$\widetilde{(E \circ X)}(x) = 1+x$$$ for $$$X=E_1$$$ is the singleton species and $$$E$$$ is the sets species.
General formula for sets of species. Show that, generally, $$$\widetilde{(E \circ F)}(x) = \exp\left(\widetilde F(x)-\frac{\widetilde F(x^2)}{2}+\frac{\widetilde F(x^3)}{3}-\dots\right)$$$ for any species $$$F$$$.
OGF for ordered trees and balanced bracket sequences. Show that $$$B(x) = \widetilde{B}(x)$$$ and $$$\triangle(x) = \widetilde{\triangle}(x)$$$ for the ordered trees and the balanced bracket sequences.
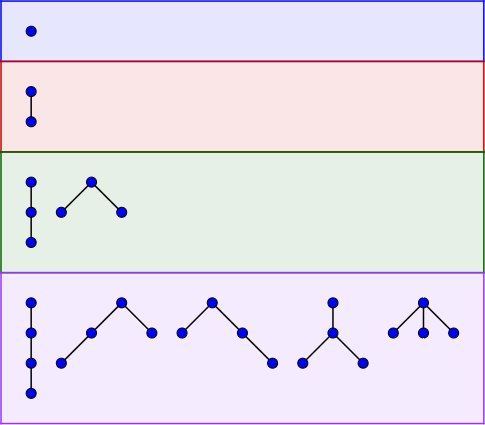
All unlabeled ordered trees on $$$n \in \{1,2,3,4\}$$$ vertices.
The structure of the composition on unlabeled structures is a topic of interest in itself and can be found in a more or less general form with the so-called cycle index series, which in turn leads to the Pólya enumeration theorem (which generalizes Burnside's lemma). But to avoid math overload we'll leave this topic for another time.






