Sometimes I wonder, what implementation of a segment tree to use. Usually, I handwave that some will suit, and that works in most of the cases.↵
↵
But today I decided to back up the choice with some data and I ran benchmarks against 4 implementations:↵
<ul>↵
<li>↵
Simple recursive divide-and-conquer implementation↵
↵
<spoiler summary="Code">↵
~~~↵
struct SimpleRecursiveSegmentTree {↵
unsigned size;↵
↵
private:↵
std::vector<long long> t;↵
↵
void _build(const std::vector<int> &v, unsigned p, unsigned l, unsigned r) {↵
if (r == l + 1) {↵
t[p] = v[l];↵
return;↵
}↵
unsigned m = (l + r) / 2;↵
_build(v, 2 * p + 1, l, m);↵
_build(v, 2 * p + 2, m, r);↵
t[p] = t[2 * p + 1] + t[2 * p + 2];↵
}↵
↵
long long _get(unsigned p, unsigned l, unsigned r, unsigned a,↵
unsigned b) const {↵
if (b <= l || r <= a) {↵
return 0LL;↵
}↵
if (a <= l && r <= b) {↵
return t[p];↵
}↵
unsigned m = (l + r) / 2;↵
return _get(2 * p + 1, l, m, a, b) + _get(2 * p + 2, m, r, a, b);↵
}↵
↵
void _add(unsigned p, unsigned l, unsigned r, unsigned i, int x) {↵
if (i < l || r <= i) {↵
return;↵
}↵
if (r == l + 1) {↵
t[p] += x;↵
return;↵
}↵
unsigned m = (l + r) / 2;↵
_add(2 * p + 1, l, m, i, x);↵
_add(2 * p + 2, m, r, i, x);↵
t[p] = t[2 * p + 1] + t[2 * p + 2];↵
}↵
↵
public:↵
SimpleRecursiveSegmentTree(unsigned _size) noexcept : size(_size) {↵
t.resize(4 * size);↵
}↵
↵
SimpleRecursiveSegmentTree(const std::vector<int> &v) noexcept↵
: size(v.size()) {↵
t.resize(4 * size);↵
_build(v, 0, 0, size);↵
}↵
↵
void add(unsigned i, int x) { _add(0, 0, size, i, x); }↵
↵
long long get(unsigned l, unsigned r) const {↵
return _get(0, 0, size, l, r);↵
}↵
};↵
~~~↵
</spoiler>↵
↵
</li>↵
<li>↵
Optimized recursive divide-and-conquer, which does not descend into apriori useless branches↵
↵
<spoiler summary="Code">↵
~~~↵
struct OptimizedRecursiveSegmentTree {↵
unsigned size;↵
↵
private:↵
std::vector<long long> t;↵
↵
void _build(const std::vector<int> &v, unsigned p, unsigned l, unsigned r) {↵
if (r == l + 1) {↵
t[p] = v[l];↵
return;↵
}↵
unsigned m = (l + r) / 2;↵
_build(v, 2 * p + 1, l, m);↵
_build(v, 2 * p + 2, m, r);↵
t[p] = t[2 * p + 1] + t[2 * p + 2];↵
}↵
↵
long long _get(unsigned p, unsigned l, unsigned r, unsigned a,↵
unsigned b) const {↵
if (a <= l && r <= b) {↵
return t[p];↵
}↵
unsigned m = (l + r) / 2;↵
long long res = 0;↵
if (a < m) {↵
res += _get(2 * p + 1, l, m, a, b);↵
}↵
if (b > m) {↵
res += _get(2 * p + 2, m, r, a, b);↵
}↵
return res;↵
}↵
↵
void _add(unsigned p, unsigned l, unsigned r, unsigned i, int x) {↵
if (r == l + 1) {↵
t[p] += x;↵
return;↵
}↵
unsigned m = (l + r) / 2;↵
if (i < m) {↵
_add(2 * p + 1, l, m, i, x);↵
} else {↵
_add(2 * p + 2, m, r, i, x);↵
}↵
t[p] = t[2 * p + 1] + t[2 * p + 2];↵
}↵
↵
public:↵
OptimizedRecursiveSegmentTree(unsigned _size) noexcept : size(_size) {↵
t.resize(4 * size);↵
}↵
↵
OptimizedRecursiveSegmentTree(const std::vector<int> &v) noexcept↵
: size(v.size()) {↵
t.resize(4 * size);↵
_build(v, 0, 0, size);↵
}↵
↵
void add(unsigned i, int x) { _add(0, 0, size, i, x); }↵
↵
long long get(unsigned l, unsigned r) const {↵
return _get(0, 0, size, l, r);↵
}↵
};↵
~~~↵
</spoiler>↵
↵
</li>↵
<li>↵
Non-recursive implementation (credits: https://mirror.codeforces.com/blog/entry/18051)↵
↵
<spoiler summary="Code">↵
~~~↵
struct NonRecursiveSegmentTree {↵
unsigned size;↵
↵
private:↵
std::vector<long long> t;↵
↵
void _build(const std::vector<int> &v) {↵
std::copy(v.begin(), v.end(), t.begin() + size);↵
for (int i = size - 1; i > 0; --i) {↵
t[i] = t[i * 2] + t[i * 2 ^ 1];↵
}↵
}↵
↵
public:↵
NonRecursiveSegmentTree(unsigned _size) noexcept : size(_size) {↵
t.resize(2 * size);↵
}↵
↵
NonRecursiveSegmentTree(const std::vector<int> &v) noexcept↵
: size(v.size()) {↵
t.resize(2 * size);↵
_build(v);↵
}↵
↵
void add(unsigned i, int x) {↵
i += size;↵
for (t[i] += x; i > 1; i /= 2) {↵
t[i / 2] = t[i] + t[i ^ 1];↵
}↵
}↵
↵
long long get(unsigned l, unsigned r) const {↵
long long res = 0;↵
for (l += size, r += size; l < r; l /= 2, r /= 2) {↵
if (l & 1) {↵
res += t[l++];↵
}↵
if (r & 1) {↵
res += t[--r];↵
}↵
}↵
return res;↵
}↵
};↵
~~~↵
</spoiler>↵
↵
</li>↵
<li>↵
Fenwick Tree↵
↵
<spoiler summary="Code">↵
~~~↵
struct FenwickTree {↵
unsigned size;↵
↵
private:↵
std::vector<long long> t;↵
↵
long long get_prefix(int i) const {↵
long long res = 0;↵
while (i >= 0) {↵
res += t[i];↵
i = (i & (i + 1)) - 1;↵
}↵
return res;↵
}↵
↵
public:↵
void add(unsigned i, int x) {↵
while (i < size) {↵
t[i] += x;↵
i = i | (i + 1);↵
}↵
}↵
↵
FenwickTree(unsigned _size) : size(_size) { t.resize(size); }↵
↵
FenwickTree(const std::vector<int> &v) : size(v.size()) {↵
t.resize(size);↵
for (unsigned i = 0; i < size; ++i) {↵
add(i, v[i]);↵
}↵
}↵
↵
long long get(unsigned l, unsigned r) {↵
return get_prefix((int)r - 1) - get_prefix((int)l - 1);↵
}↵
};↵
~~~↵
</spoiler>↵
↵
</li>↵
</ul>↵
↵
All implementations are able to:↵
<ul>↵
<li>↵
`get(l, r)`: get sum on a segment (half-interval) $[l; r)$↵
</li>↵
<li>↵
`add(i, x)`: add $x$ to the element by index $i$↵
</li>↵
</ul>↵
↵
Here are the results:↵
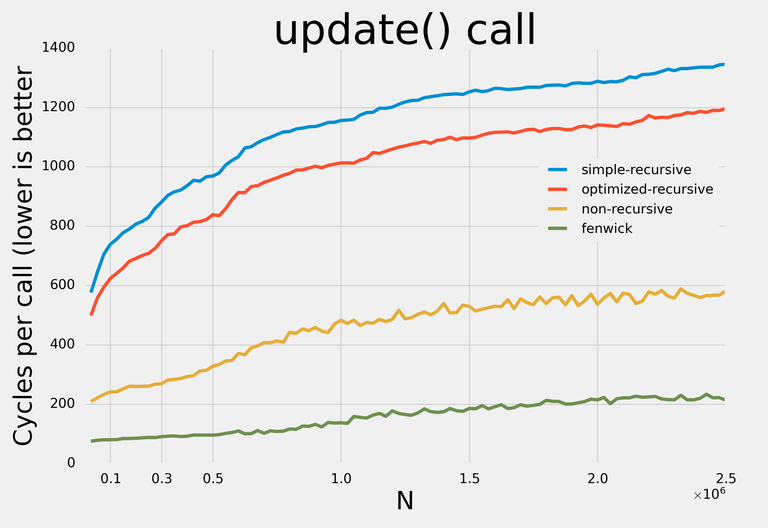↵
↵
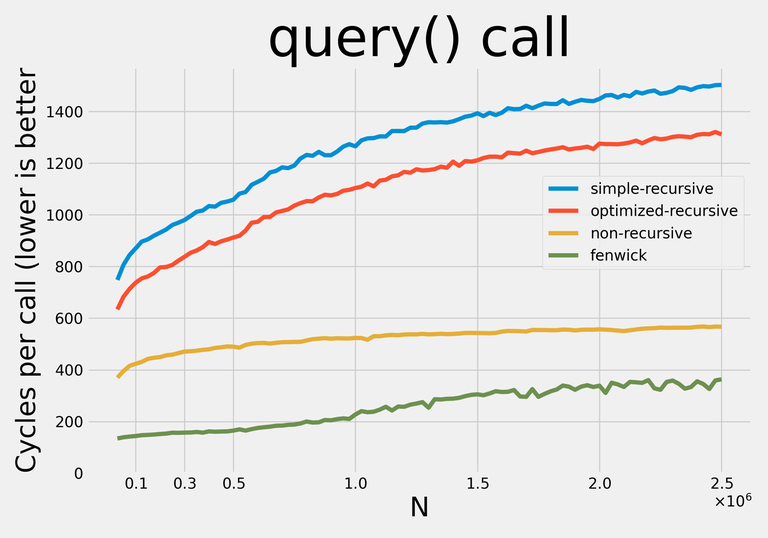↵
↵
Note: I decided not to apply any addition-specific optimizations so that with minor modifications the data structures could be used for any supported operations.↵
↵
I generated queries the following way:↵
↵
- Update: generate random index (`rnd() % size`) and number↵
- Query: at first, generate random length (`rnd() % size + 1`), then generate a left border for that length↵
↵
[Benchmarking source code](https://gist.github.com/pavel-the-best/35e1bf7759152c442f3c83d721947e97#file-bench-cpp). Note that ideally you should disable frequency scaling and, close any applications that might disrupt the benchmark (basically, the more you close — the better) and pin the benchmark process to a single CPU (core).↵
↵
[Plot-generating Python script](https://gist.github.com/pavel-the-best/8636aeb68db2119b00fce679d361df6f#file-generate_plot-py)↵
↵
[My benchmarking data](https://gist.github.com/pavel-the-best/f33879ea075b5e9b3ea16e4d85d807dd) in case you want to do some more plotting/comparing.↵
↵
I compiled the benchmark with `#pragma GCC optimize("O3")` on GNU GCC 11.3.0, and ran it with the CPU fixed on 2.4 GHz without, the process pinned on a single CPU core and the desktop environment openclosed.↵
↵
This is probably my first useful contribution so any suggestions/improvements are welcome.↵
↵
But today I decided to back up the choice with some data and I ran benchmarks against 4 implementations:↵
<ul>↵
<li>↵
Simple recursive divide-and-conquer implementation↵
↵
<spoiler summary="Code">↵
~~~↵
struct SimpleRecursiveSegmentTree {↵
unsigned size;↵
↵
private:↵
std::vector<long long> t;↵
↵
void _build(const std::vector<int> &v, unsigned p, unsigned l, unsigned r) {↵
if (r == l + 1) {↵
t[p] = v[l];↵
return;↵
}↵
unsigned m = (l + r) / 2;↵
_build(v, 2 * p + 1, l, m);↵
_build(v, 2 * p + 2, m, r);↵
t[p] = t[2 * p + 1] + t[2 * p + 2];↵
}↵
↵
long long _get(unsigned p, unsigned l, unsigned r, unsigned a,↵
unsigned b) const {↵
if (b <= l || r <= a) {↵
return 0LL;↵
}↵
if (a <= l && r <= b) {↵
return t[p];↵
}↵
unsigned m = (l + r) / 2;↵
return _get(2 * p + 1, l, m, a, b) + _get(2 * p + 2, m, r, a, b);↵
}↵
↵
void _add(unsigned p, unsigned l, unsigned r, unsigned i, int x) {↵
if (i < l || r <= i) {↵
return;↵
}↵
if (r == l + 1) {↵
t[p] += x;↵
return;↵
}↵
unsigned m = (l + r) / 2;↵
_add(2 * p + 1, l, m, i, x);↵
_add(2 * p + 2, m, r, i, x);↵
t[p] = t[2 * p + 1] + t[2 * p + 2];↵
}↵
↵
public:↵
SimpleRecursiveSegmentTree(unsigned _size) noexcept : size(_size) {↵
t.resize(4 * size);↵
}↵
↵
SimpleRecursiveSegmentTree(const std::vector<int> &v) noexcept↵
: size(v.size()) {↵
t.resize(4 * size);↵
_build(v, 0, 0, size);↵
}↵
↵
void add(unsigned i, int x) { _add(0, 0, size, i, x); }↵
↵
long long get(unsigned l, unsigned r) const {↵
return _get(0, 0, size, l, r);↵
}↵
};↵
~~~↵
</spoiler>↵
↵
</li>↵
<li>↵
Optimized recursive divide-and-conquer, which does not descend into apriori useless branches↵
↵
<spoiler summary="Code">↵
~~~↵
struct OptimizedRecursiveSegmentTree {↵
unsigned size;↵
↵
private:↵
std::vector<long long> t;↵
↵
void _build(const std::vector<int> &v, unsigned p, unsigned l, unsigned r) {↵
if (r == l + 1) {↵
t[p] = v[l];↵
return;↵
}↵
unsigned m = (l + r) / 2;↵
_build(v, 2 * p + 1, l, m);↵
_build(v, 2 * p + 2, m, r);↵
t[p] = t[2 * p + 1] + t[2 * p + 2];↵
}↵
↵
long long _get(unsigned p, unsigned l, unsigned r, unsigned a,↵
unsigned b) const {↵
if (a <= l && r <= b) {↵
return t[p];↵
}↵
unsigned m = (l + r) / 2;↵
long long res = 0;↵
if (a < m) {↵
res += _get(2 * p + 1, l, m, a, b);↵
}↵
if (b > m) {↵
res += _get(2 * p + 2, m, r, a, b);↵
}↵
return res;↵
}↵
↵
void _add(unsigned p, unsigned l, unsigned r, unsigned i, int x) {↵
if (r == l + 1) {↵
t[p] += x;↵
return;↵
}↵
unsigned m = (l + r) / 2;↵
if (i < m) {↵
_add(2 * p + 1, l, m, i, x);↵
} else {↵
_add(2 * p + 2, m, r, i, x);↵
}↵
t[p] = t[2 * p + 1] + t[2 * p + 2];↵
}↵
↵
public:↵
OptimizedRecursiveSegmentTree(unsigned _size) noexcept : size(_size) {↵
t.resize(4 * size);↵
}↵
↵
OptimizedRecursiveSegmentTree(const std::vector<int> &v) noexcept↵
: size(v.size()) {↵
t.resize(4 * size);↵
_build(v, 0, 0, size);↵
}↵
↵
void add(unsigned i, int x) { _add(0, 0, size, i, x); }↵
↵
long long get(unsigned l, unsigned r) const {↵
return _get(0, 0, size, l, r);↵
}↵
};↵
~~~↵
</spoiler>↵
↵
</li>↵
<li>↵
Non-recursive implementation (credits: https://mirror.codeforces.com/blog/entry/18051)↵
↵
<spoiler summary="Code">↵
~~~↵
struct NonRecursiveSegmentTree {↵
unsigned size;↵
↵
private:↵
std::vector<long long> t;↵
↵
void _build(const std::vector<int> &v) {↵
std::copy(v.begin(), v.end(), t.begin() + size);↵
for (int i = size - 1; i > 0; --i) {↵
t[i] = t[i * 2] + t[i * 2 ^ 1];↵
}↵
}↵
↵
public:↵
NonRecursiveSegmentTree(unsigned _size) noexcept : size(_size) {↵
t.resize(2 * size);↵
}↵
↵
NonRecursiveSegmentTree(const std::vector<int> &v) noexcept↵
: size(v.size()) {↵
t.resize(2 * size);↵
_build(v);↵
}↵
↵
void add(unsigned i, int x) {↵
i += size;↵
for (t[i] += x; i > 1; i /= 2) {↵
t[i / 2] = t[i] + t[i ^ 1];↵
}↵
}↵
↵
long long get(unsigned l, unsigned r) const {↵
long long res = 0;↵
for (l += size, r += size; l < r; l /= 2, r /= 2) {↵
if (l & 1) {↵
res += t[l++];↵
}↵
if (r & 1) {↵
res += t[--r];↵
}↵
}↵
return res;↵
}↵
};↵
~~~↵
</spoiler>↵
↵
</li>↵
<li>↵
Fenwick Tree↵
↵
<spoiler summary="Code">↵
~~~↵
struct FenwickTree {↵
unsigned size;↵
↵
private:↵
std::vector<long long> t;↵
↵
long long get_prefix(int i) const {↵
long long res = 0;↵
while (i >= 0) {↵
res += t[i];↵
i = (i & (i + 1)) - 1;↵
}↵
return res;↵
}↵
↵
public:↵
void add(unsigned i, int x) {↵
while (i < size) {↵
t[i] += x;↵
i = i | (i + 1);↵
}↵
}↵
↵
FenwickTree(unsigned _size) : size(_size) { t.resize(size); }↵
↵
FenwickTree(const std::vector<int> &v) : size(v.size()) {↵
t.resize(size);↵
for (unsigned i = 0; i < size; ++i) {↵
add(i, v[i]);↵
}↵
}↵
↵
long long get(unsigned l, unsigned r) {↵
return get_prefix((int)r - 1) - get_prefix((int)l - 1);↵
}↵
};↵
~~~↵
</spoiler>↵
↵
</li>↵
</ul>↵
↵
All implementations are able to:↵
<ul>↵
<li>↵
`get(l, r)`: get sum on a segment (half-interval) $[l; r)$↵
</li>↵
<li>↵
`add(i, x)`: add $x$ to the element by index $i$↵
</li>↵
</ul>↵
↵
Here are the results:↵
↵
↵
Note: I decided not to apply any addition-specific optimizations so that with minor modifications the data structures could be used for any supported operations.↵
↵
I generated queries the following way:↵
↵
- Update: generate random index (`rnd() % size`) and number↵
- Query: at first, generate random length (`rnd() % size + 1`), then generate a left border for that length↵
↵
[Benchmarking source code](https://gist.github.com/pavel-the-best/35e1bf7759152c442f3c83d721947e97#file-bench-cpp). Note that ideally you should disable frequency scaling
↵
[Plot-generating Python script](https://gist.github.com/pavel-the-best/8636aeb68db2119b00fce679d361df6f#file-generate_plot-py)↵
↵
[My benchmarking data](https://gist.github.com/pavel-the-best/f33879ea075b5e9b3ea16e4d85d807dd) in case you want to do some more plotting/comparing.↵
↵
I compiled the benchmark with `#pragma GCC optimize("O3")` on GNU GCC 11.3.0, and ran it with the CPU fixed on 2.4 GHz
↵
This is probably my first useful contribution so any suggestions/improvements are welcome.↵






