This (quite sudden) post is about a data structure I have came up with in one day in bed, and this won't be a full series(I am yet a student, which means I don't have time to invent data structures all day and all night). Still, Thinking about this, I thought it would be a good idea to cover it on its own post. So here we are.
Concept
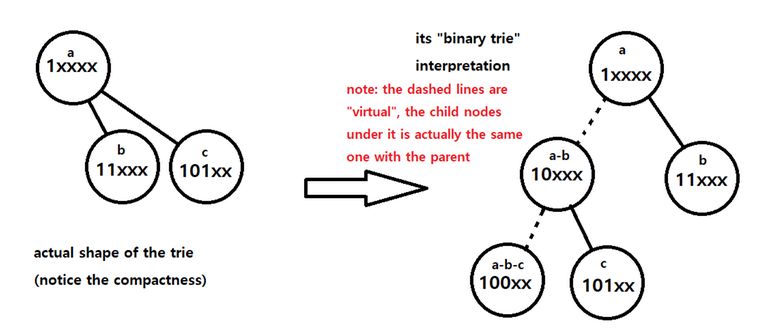
The traditional bit trie uses one leaf node for one number, and every leaf node has same depth. but about this, I thought — why? "Do we really have to use $$$32$$$ zeroes, just to represent a single zero? Heck no. There has to be a better way." And this is where I came up with this idea.
Instead of using the same old left-right child, let's use up to $$$l \leq depth$$$ children for one node. $$$l$$$ is the suffix part when each node represents a prefix. For every prefix node, we connect prefix nodes with only one $$$1$$$ bit determined after the current prefix. For example, under $$$1\text{xxxx}_2$$$, there are $$$11\text{xxx}_2$$$, $$$101\text{xx}_2$$$, and etc. Then, while the undetermined suffix (ex. the $$$\text{xxx}$$$ in $$$1\text{xxx}_2$$$) is, of course, undetermined, we can assume they are $$$0$$$ for the exact node the prefix exists on. Then we can use the prefix node $$$1\text{xxxx}_2$$$ for $$$10000_2$$$ also.
The Important Detail
At this moment, you should be wondering, how do we distinguish the node for the number $$$10000_2$$$ and the prefix $$$1\text{xxxx}_2$$$? They use the same node after all. My conclusion? You don't need to. To do this, you can just save the size (amount of elements) of the subtree. Now, let us denote the size of the subtree of prefix $$$S$$$ as $$$n(S)$$$. then $$$n(1\text{xxxx}_2) = n(11\text{xxx}_2) + n(101\text{xx}_2) + \ldots + n(10000_2)$$$ applies. So you can just traverse the child nodes one by one, and the rest is the number itself.
Traversing the Bit-indexed Trie
Using the "important detail" stated above, traversing the Bit-indexed Trie boils down to simply interpreting it like a binary tree. We start at the root, which is $$$0$$$, and we can interpret this node as $$$0\text{xxxxx}_2$$$. This root node may (or may not) have $$$01\text{xxxx}_2$$$ as a child node. Important point here is to keep a variable for the size of the "virtual" subtree of the current node. (we will denote this as $$$c$$$.) If the subtree size of the current node ($$$0\text{xxxxx}_2$$$) is $$$s$$$ and that of the right child node ($$$01\text{xxxx}_2$$$) is $$$s_1$$$, then the subtree size of the left child node, when interpreted as a binary trie, should be $$$s-s_1$$$. So if we want to traverse towards the right child node, do so, and update $$$c$$$ to $$$s_1$$$. On the other hand, if we want to traverse towards the left child node, stay on the current node, assume that we did move ($$$0\text{xxxxx}_2$$$ yet shares the node with $$$00\text{xxxx}_2$$$), and update $$$c$$$ to $$$c-s_1$$$. After understanding this, almost everything goes same with the usual trie.
Interesting stuff about the Bit-indexed Trie
With the fact that a single number is represented as a single node in the data structure, we can use a hash table to represent the whole trie. And what's so great about this method? It lies in its simplicity. Let's assume the trie is represented with a unordered_map<int,int> type. (the key is for the node, the value is for the subtree size) Now inserting a value in the trie is as simple as this:
and that is it! Simple, isn't it? and here comes the reason I named the data structure "Bit-indexed Trie". Many should have noticed the similarity of the name with the Bit-indexed Tree, also known as the Fenwick Tree. (I could not call it the Fenwick Trie, Peter Fenwick simply did not make it) The Bit-indexed Trie even has many common facts with the Bit-indexed Tree! Here are some:
- It can replace the traditional bit trie, similar to how the BIT replaces the Segment Tree in many situations.
- It reduces the memory usage from $$$2M$$$ ~ $$$4M$$$ to $$$M$$$, as they save values in every node, not only the leaf nodes.
- They have very similar implementation in many parts, see the snippet above.
also, as we saved the subtree sizes, accessing the subtree size information turns out to be almost $$$O(1)$$$ (assuming the nodes are saved in a data structure with $$$O(1)$$$ random access). Even if you don't make it $$$O(1)$$$, I believe the improvements will be quite significant, as it would be possible to optimize some processes with __builtin_clz and such bitmask functions.
EDIT: errorgorn and Kaey told me that finding the amount of numbers with a certain prefix is not $$$O(1)$$$, and he is correct. It turns out to be $$$O(\text{number of trailing zeroes in the prefix})$$$.
Summary
In this post, I covered the concepts and details of the data structure I have come up with, which makes it possible to reduce the memory usage in a bit-trie to half of the usual trie or even further. I look forward to release a full C++ implementation of it soon, and I hope many people would notice the beauty of this data structure. Thank you for reading.






