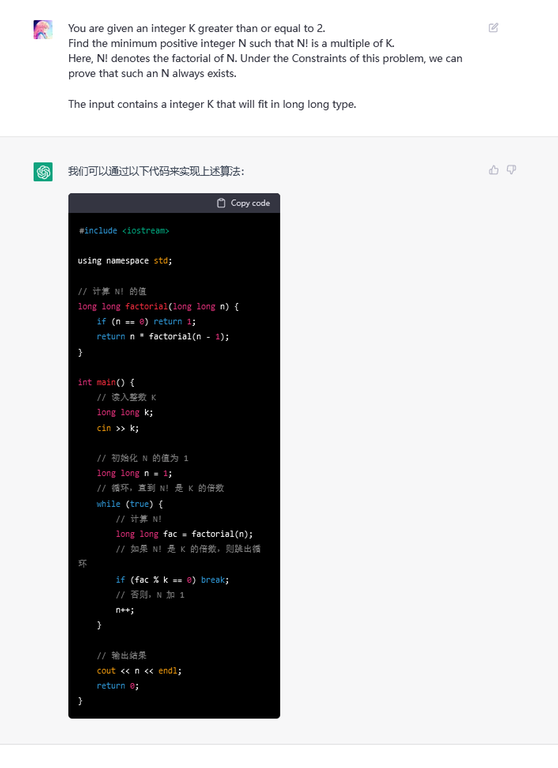
You are given an integer $$$K$$$ greater than or equal to $$$2$$$. Find the minimum positive integer $$$N$$$ such that $$$N!$$$ is a multiple of $$$K$$$.
Here, $$$N!$$$ denotes the factorial of $$$N$$$. Under the Constraints of this problem, we can prove that such an $$$N$$$ always exists.
Constraint: $$$2 \leq K \leq 10 ^12$$$
Here are the interactions. ChatGPT spoke Chinese to me (which I didn't figure out how to configure it), so I'd provide some translations here.
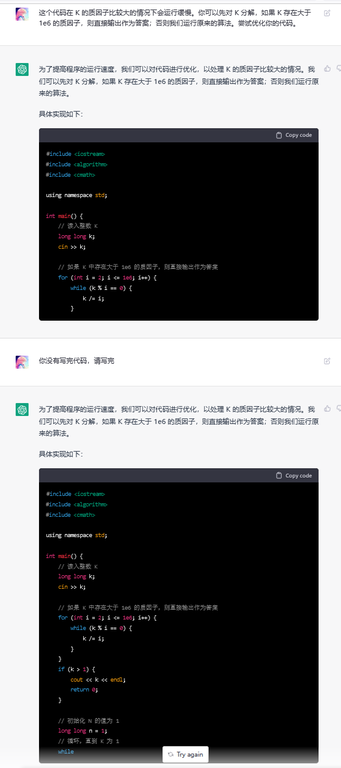
Human: (The problem statement with hint to use long long)
ChatGPT: We can use code to implement the above algorithm.
Commment: ChatGPT wrote a bruteforce algorithm that didn't notice the long long type can hardly store a factorial, which is in my expectation.
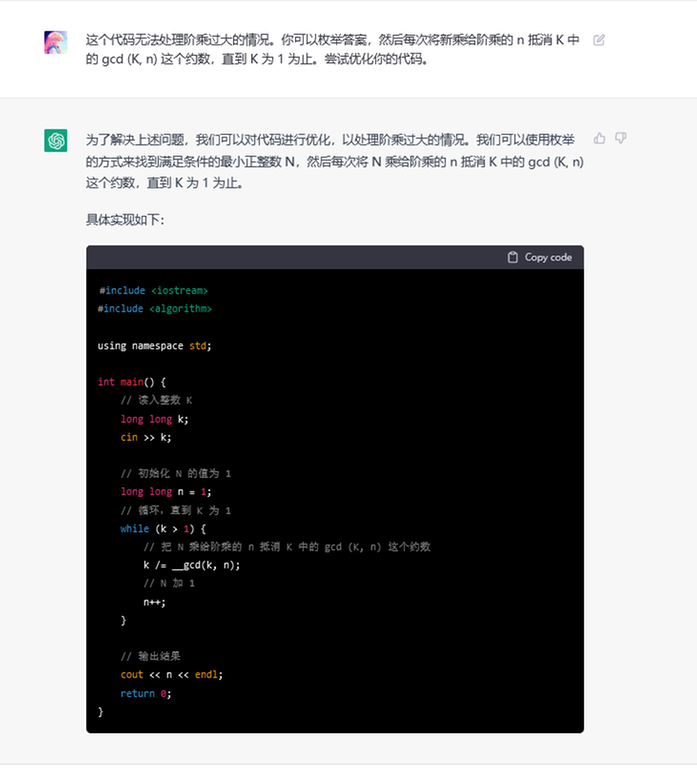
Human: This code can not process when the factorials are large. You can enumarate the answer, and when newly add $$$n$$$ to the factorial, the $$$\gcd(K, n)$$$ factor can be eliminated, until $$$K = 1$$$. Try to optimize your code.
ChatGPT: In order to solve the above problems, we can optimize the code to handle the case where the factorial is too large. We can use enumeration to find the smallest positive number N that satisfies the condition, and then offset the divisor of gcd (K, n) in K with the order n of N each time until K is 1.
The implementation is as follows. (Code follows)
Comment: !