Hello Codeforces!

Today I'll be writing about what I have learnt about combinatorics, which played, and, in my opinion, will still be playing a important role in both Codeforces and CP (short for competitive programming).

However, combinatorics is such a great subject that made that impossible for me to write it all in one blog. So, this is just the second blog, which is friendly to beginners. If you are interested, please, pay attention to this account and I'll give posts as series for a long term.

If you have found some mistakes in the text, or if you have some questions about the topic, please, leave a comment, and I'll check it weekly and reply. Also, if you find some grammar mistakes, a kind comment will be also welcomed.

Previous Blogs

• Combinatorics (1)

Blogs in the future

If finished, I'll link them.

• Combinatorics (3)
• Bitmask
• Probabilities

Content

1. Quick power
2. Fermat's little theorem
3. extent-gcd
4. The multiplicative inverse of an integer
5. Prework optimize
6. homework

Part 1 — Quick power

How to calculate the value of $$$a^b\bmod p$$$?

You may write out this code easily:

long long power(long long a, long long b, long long p) {
	long long res = 1;
	while(b--) res = res * a % p;
	return res;
}

Seems easy, right? This code has $$$\mathcal O(b)$$$ time complexity. But what if $$$1\leq a,b\leq 10^9$$$? Can you solve it?

Here, we use divide ans conquer to solve this:

According to this, we can write out a code easily:

long long powpow(long long a, long long b, long long p) {
	if(b % 2 == 1) {
		long long r = powpow(a, b / 2, p);
		return r * r % p * a % p;
	} else {
		long long r = powpow(a, b / 2, p);
		return r * r % p;
	}
}

Now certainly the time complexity is $$$\mathcal O(\log b)$$$. But this code contains a recursion. Since the recursion is simple, we can get rid of recursion:

long long quickpow(long long a, long long b, long long p) {
	long long res = 1, nowa = 1;
	while(b) {
		if(b % 2 == 1) res = res * nowa % p;
		nowa = a * a % p;
		a = nowa;
		b /= 2;
	}
	return res;
}

Now I'll give a fast version of it without explaining, you can use it in the later implementaions.

long long quickpow(long long a, long long b, long long p) {
	long long res = 1;
	while(b) {
		if(b & 1) res = res * a % p;
		a = a * a % p;
		b >>= 1;
	}
	return res;
}

The time complexity remains the same, but the constant is smaller now. If you still wonders why, you can wait for my bitmask post.

Exercise: Calculate $$$(a\times b) \bmod p$$$, $$$10^9 \leq p\leq 10^{18}$$$.

In C++, long long varible is between $$$-2^{63}$$$ and $$$2^{63}-1$$$, which is about $$$10^{18}$$$. When you do a * b % p, then things below will happen:

• $$$a\times b$$$ is calculated first, it can overflow and lead to error.
• $$$a\times b\bmod p$$$ is calculated, the result is already wrong.

So multiply it with brute force is impossible, can you think of an $$$\mathcal O(\log b)$$$ solution?

long long quickpow(long long a, long long b, long long p) {
	long long res = 1;
	while(b) {
		if(b & 1) res = (res + a) % p;
		a = (a + a) % p;
		b >>= 1;
	}
	return res;
}

You may wonder, if we divide it into $$$2$$$ parts, why don't we divide it into $$$k$$$ parts?

Actually, the time complexity is $$$\mathcal O(k\times\log_{k} n)$$$.

Look at the image we draw out $$$y=k+k\times \log_{k}(8\times 10^9)$$$:

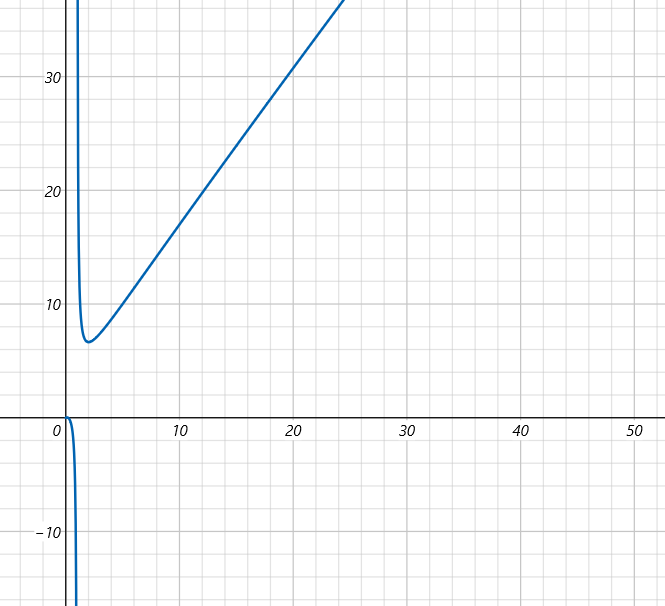
And we draw out $$$\color{green} {x=2}$$$ and $$$\color{red}{x=3}$$$:

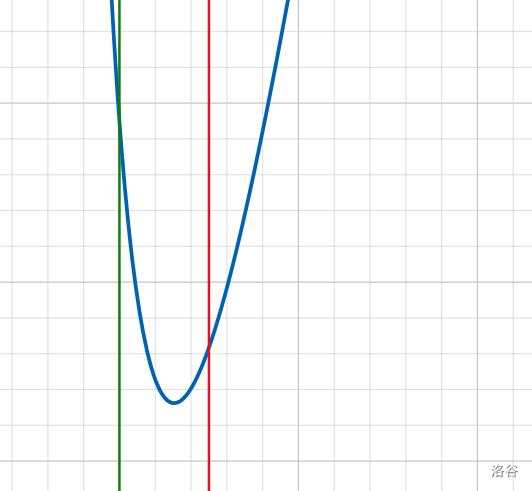
So we find that $$$k=2,3$$$ is optimal. But $$$k=3$$$ uses $$$3$$$ if sentences, this lead to larger constant than expected, so we use $$$k=2$$$ instead.