Problem: Rectangle Shrinking

Part 1: Notations

$$$x$$$: A brick. $$$x_i$$$ denotes the part of $$$x$$$ belonging to the $$$i$$$-th floor. For example, if $$$x.u=1,\,x.d=2$$$, then $$$x_1.u=x_1.d=1$$$, $$$x_2.u=x_2.d=2$$$, and $$$x_1.l=x_2.l=x.l$$$, $$$x_1.r=x_2.r=x.r$$$.

$$$A_i,\,i=1,2$$$: The set of bricks whose $$$u=d=i$$$.

$$$B$$$: The set of bricks whose $$$u=1,\,d=2$$$.

$$$\texttt{Remove}$$$: Remove a brick $$$x$$$.

$$$\texttt{Shrink}$$$: Shrink a brick $$$x$$$ to another non-empty brick.

$$$\texttt{Keep}$$$: Keep a brick $$$x$$$ unchanged.

Note that in our solution we may operate on a part of brick. For example, for a brick $$$x \in B$$$, we may $$$\texttt{Keep}\,x_1$$$ while $$$\texttt{Remove}\,x_2$$$.

Part 2: Idea

I think $$$\texttt{Shrink}$$$ing $$$x \in B$$$ is troublesome. If you shrink $$$x_1$$$, you have to shrink $$$x_2$$$ in the same way, i.e., $$$x_1$$$ has to be aligned with $$$x_2$$$. So is there a solution that only performs $$$\texttt{Remove}$$$ and $$$\texttt{Keep}$$$ on every $$$x \in B$$$? But that is impossible, because the bricks $$$x, y \in B$$$ may overlap themselves even with considering $$$A$$$. So what if $$$B$$$ are pairwise non-overlapping (because we could perform some pre-$$$\texttt{Shrink}$$$ and pre-$$$\texttt{Remove}$$$ to make $$$B$$$ pairwise non-overlapping)? [Pre-computation]

In that case, we can consider each floor independently. Let

$$$C_i := A_i \cup \{x_i \mid x \in B \}$$$.

For example, if

$$$A_1 = \{[u=1, d=1, l=2, r=5], [u=1, d=1, l=7, r=10]\}$$$,

$$$B=\{[u=1, d=2, l=2, r=2], [u=1, d=2, l=4, r=7]\}$$$, then

$$$C_1 = \{[u=1, d=1, l=2, r=2], [u=1, d=1, l=2, r=5], [u=1, d=1, l=4, r=7], [u=1, d=1, l=7, r=10]\}$$$.

We sort $$$C_i$$$ w.r.t $$$l$$$, and traverse $$$C_i$$$ like $$$\texttt{for(auto x: C_i)}$$$.

Case 1 ($$$\texttt{Keep}$$$): If $$$x$$$ is not overlapping now, then we add $$$x$$$ to the answer, no matter if $$$x$$$ is from $$$A_i$$$ or not.

Case 2 ($$$\texttt{Remove}$$$): If $$$x$$$ is fully contained in the union of other rectangles, then we always remove $$$x$$$, no matter if $$$x$$$ is from $$$A_i$$$ or not.

$$$\texttt{Keep}$$$ and $$$\texttt{Remove}$$$ are relatively easier, no matter $$$x \in A_i$$$ or $$$x \in \{x_i \mid x \in B \}$$$.

Case 3 ($$$\texttt{Shrink}$$$): If $$$x$$$ is partially overlapping with other bricks.

Case 3.1: If $$$x \in A_i$$$: $$$\texttt{Shrink} x$$$. Move the $$$x.l$$$ to the right to avoid overlapping.

Case 3.2: If $$$x \in \{x_i \mid x \in B \}$$$: $$$\texttt{Shrink}$$$ all bricks that overlap with $$$x$$$ by moving their right endpoints (i.e., *.r), to the left.

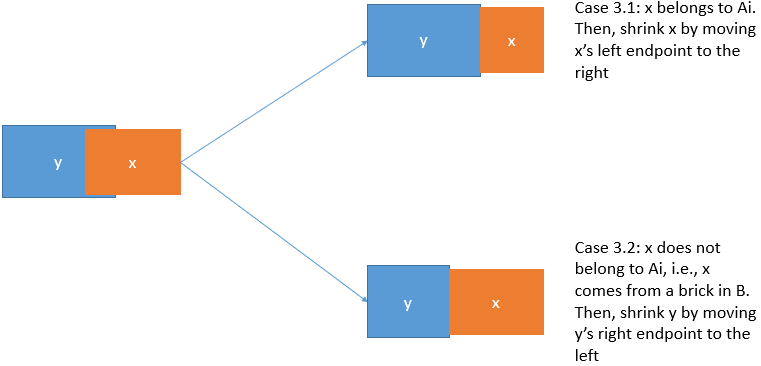
It is guaranteed in Case 3.2 that every brick overlapping with $$$x$$$ is from $$$A_i$$$ because we have already performed pre-calculations in $$$B$$$ to make them non-overlapping. The complexity is not an issue, by amortized analysis, each $$$x \in A_i$$$ will do $$$\texttt{Remove}$$$ at most once and $$$\texttt{Remove}+\texttt{Shrink}$$$ at most twice (keep/move left endpoint+keep/move right endpoint).

Part 3: Implementation

First I copy a range-set implementation from nok0. Basically, it maintains a set of intervals using $$$\texttt{std::set}$$$. When inserting/erasing a range, it can merge/split/erase intervals automatically, using binary search (Yes, stop learning useless algorithms, go to learn binary search!). It supports many APIs, here are some useful APIs in our implementation:

(1) $$$\texttt{Insert(l, r)}$$$: Insert an interval $$$[l, r]$$$.

(2) $$$\texttt{covered_by(l, r)}$$$: Return an interval covering $$$[l, r]$$$, if not exists, returning $$$(-\infty, \infty)$$$.

(3) $$$\texttt{covered(l, r)}$$$: Return a bool variable indication whether interval $$$[l, r]$$$ is fully covered.

(4) $$$\texttt{right(x)}$$$: Return $$$\min \{y|y \geq x, y \text{ is not covered}\}$$$. Note that API could calculate the $$$\texttt{mex}$$$, so it is also useful for calculating the Sprague-Grundy (SG) number. SG number is irrelevant to our topic.

(5) $$$\texttt{left(x)}$$$ (added by me): Return $$$\max \{y|y \leq x, y \text{ is not covered}\}$$$.

There are also APIs that we don't use in this implementation, but they are also beneficial:

(6) $$$\texttt{Erase(l, r)}$$$: Erase $$$[l, r]$$$. That may lead to interval splitting, for example, if we erase $$$[2, 3]$$$ from $$$[1, 4]$$$, we get two intervals remaining: $$$[1, 1]$$$ and $$$[4, 4]$$$.

(7) $$$\texttt{size}$$$: Get the size of intervals.

(8) $$$\texttt{dump}$$$: Output all intervals for debugging.

So, we implement the pre-computation step (first paragraph in Part2) as follows:

sort B w.r.t l (left endpoint).
Initial a range set named rs.
for(auto& x: B){
    int rightl = rs.right(x.l), leftr = rs.left(x.r);
    if(right <= rightr){
        rs.insert(rightl, leftr);
        for(int i = 1; i <= 2; ++i)  {
             Ci = Ai; Ci.push_back({x.u, x.rightl, x.d, x.leftr, x.id}); //push into Ci
        }
    }else{
        //Case 2, fully contained, remove it!
        //We actually do nothing here
    }
}  

Then, how to calculate $$$C_i$$$ from each floor independently? We need another set that is sorted by $$$r$$$ in the ascending order, let's call it $$$\texttt{sortbyr}$$$, to maintain rectangles in $$$A_i \subseteq C_i$$$. If Case 3.2 happens, we need to find such $$$y \in \texttt{sortbyr}$$$ quickly by $$$\texttt{sortbyr.lower_bound(x.l)}$$$, i.e., find an interval $$$y \in A_i$$$ quickly, using binary search, such that the right endpoint of $$$y$$$ ($$$y.r$$$) is greater or equal than $$$x.l$$$. Note that when we find such an $$$y$$$, you need to iterate to the end of $$$\texttt{sortbyr}$$$, that's why my previous submissions WA at test15--I only handle one of them. Here is the sketch of the implementation:

for(int i = 1; i <= 2; ++i){
    Initialize sortbyr; //Remember to initialize because we handle each floor independently!
    sort(Ci.begin(), Ci.end());
    Initial a range set named rs.
    for(auto x: Ci){
         bool lcovered = rs.covered(l), rcovered = rs.covered(r);
         if(!lcovered && !rcovered){
             //Case 1, Keep
             if(u == d){
                sortbyr.insert({x.u, x.l, x.d, x.r, x.id});
             }
             ans[x.id].insert(node{j+1, x.l, j+1, x.r, x.id}); //No matter u == d or u != d, we only consider one floor here!
             rs.insert(x.l, x.r);
         }else if(lcovered && !recovered){
             if(u == d){
                 //Case 3.1
                 int rightl = rs.right(l);
                 ans[x.id].insert(x.u, x.rightl, x.d, x.r, x.id);
                 rs.insert(rightl, x.r);
                 sortbyr.insert(x.u, x.rightl, x.d, x.r, x.id});
             }else{
                 //Case 3.2
                 auto y = sortbyr.lower_bound({-1, -1, -1, x.l, -1});
                 while(y != sortbyr.end()){
                     //Here, we should deal with all overlaps! That's why my previous submissions WA on test15
                     auto [u2, l2, d2, r2, id2] = *y;
                     //Here l2 <= l because we sort Ci by l. So sortbyr only contains elements whose left endpoint <= l!
                     //By lower_bound, we have r2 >= x.l
                     ans[id2].erase({u2, l2, d2, r2, id2}); //We erase it from our answer
                     sortbyr.erase(y++);
                     ans[x.id].insert({j+1, x.l, j+1, x.r, x.id}); //We never shrink the splitted ones
                     rs.insert(x.l, x.r); //Although [l, r] overlaps with [l2, r2], range set will merge them automatically!
                     if(l2 <= l-1){ //Be careful! r2 may <= r, so y after shrinking may be empty!! 
                         ans[id2].insert({u2, l2, d2, x.l-1, id2});
                         sortbyr.insert({u2, l2, d2, x.l-1, id2});
                     }
                 }
             }//Case 3.2
         }//Case 3
    }//for
}

In the above implementation, it is not possible that $$$\texttt{!lcovered && rcovered}$$$, otherwise $$$[l, r]$$$ is covered by some $$$[l_1, r_1]$$$ which $$$l_1 > l$$$. But we have already sorted $$$C_i$$$ by $$$l$$$. And, if $$$l$$$ and $$$r$$$ are both covered, we just ignore and \texttt{Remove} this segment.

Finally, we need to output the answer, for this part please refer to the code. Note that due to the implementation, we may insert two parts of bricks for $$$b \in B$$$. I mean, for $$$x = \{1, l, 2, r, id\} \in B$$$, the implementation might insert both $$$\{1, l, 1, r, id\}$$$ and $$$\{2, l, 2, r, id\}$$$ into $$$ans[id]$$$, so we need to merge them manually, that is dirty work.

Here is an advertisement for CFStress: Although my previous submission WA on case5 of test15, CFStress could still find a very small counterexample in a very short time! As mentioned here, My debugging ability is really poor, so I don't use CFStress very frequently, as I often debug myself to improve my debugging ability. However, CFStress has saved me many times from insomnia. Thanks, variety-jones!