Alice and Bob are playing a game on a tree $$$T$$$ whose root is $$$1$$$. $$$T$$$ has $$$n$$$ vertices and $$$n-1$$$ edges, each vertex has an attribute $$$a \in \{1,2,3\}$$$. If $$$a=1$$$, a person on this vertex $$$v$$$ must jump to the parent of $$$v$$$, i.e., v->parent. If $$$a=2$$$, a person on this vertex $$$v$$$ must jump to $$$v$$$'s grandparent, i.e., v->parent->parent. If $$$a=3$$$, a person on this vertex can either jump to v->parent or v->parent->parent. Alice starts the first and she can choose a leaf node of $$$T$$$ to start. If somebody cannot make a move, she/he loses the game. For example, if Alice stands on a child of the root and this child has attribute $$$2$$$, then Alice loses as this child does not have a grandparent. Similarly if Bob stands on the root, he will lose as he cannot move no matter what the attribute of the root is.
Input contains $$$n+1$$$ ($$$2 \leq n \leq 10^5$$$) lines.
The first line contains a single integer $$$n$$$, which is the number of vertices.
The second line contains $$$n$$$ integers $$$a_i$$$ ($$$1 \leq a_i \leq 3$$$) representing the attribute of each vertex $$$i$$$.
The following $$$n-1$$$ lines representing edges, each line contains two integers $$$u_i$$$ and $$$v_i$$$. $$$u_i$$$-$$$v_i$$$ is an undirected edge of the tree $$$T$$$.
Output should contain $$$n-1$$$ lines, each line is a query. The $$$i$$$-th ($$$1 \leq i \leq n-1$$$) line represents the winner if Alice and Bob plays optimally when the $$$i$$$-th edge is deleted from $$$T$$$. The deletion operations are independent along queries, i.e., the $$$i$$$-th edge is recovered from deletion when you process the $$$i+1$$$-th query. Note that Alice can only choose the original leaves of $$$T$$$ as the start vertex even if the deletion operation results in new leaves.
Test case 1:
Input:
3
1 2 1
1 2
1 3
Output:
Alice
Bob
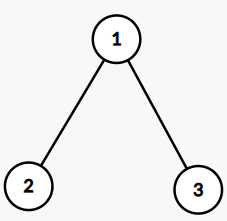
In the first line, the first edge, i.e., $$$1-2$$$ is destroyed. In this case, Alice can choose to start from vertex $$$3$$$, and jump to vertex $$$1$$$. Then, Bob will stuck at vertex $$$1$$$. Alice wins.
In the second line, the first edge $$$1-2$$$ is recovered and the second edge $$$1-3$$$ is destroyed. Here $$$3$$$ becomes an isolation vertex. If Alice starts at $$$3$$$, she cannot jump. If Alice starts at $$$2$$$, she cannot jump either as $$$2$$$ does not have grandparent. The parent of $$$2$$$ is the root $$$1$$$ but $$$1$$$ does not have a parent. Therefore, no matter where Alice starts, Bob will win.
Test case 2:
8
1 3 2 1 3 1 1 2
1 2
1 3
2 4
2 5
4 8
5 6
5 7
Output:
Alice
Bob
Bob
Alice
Bob
Bob
Bob
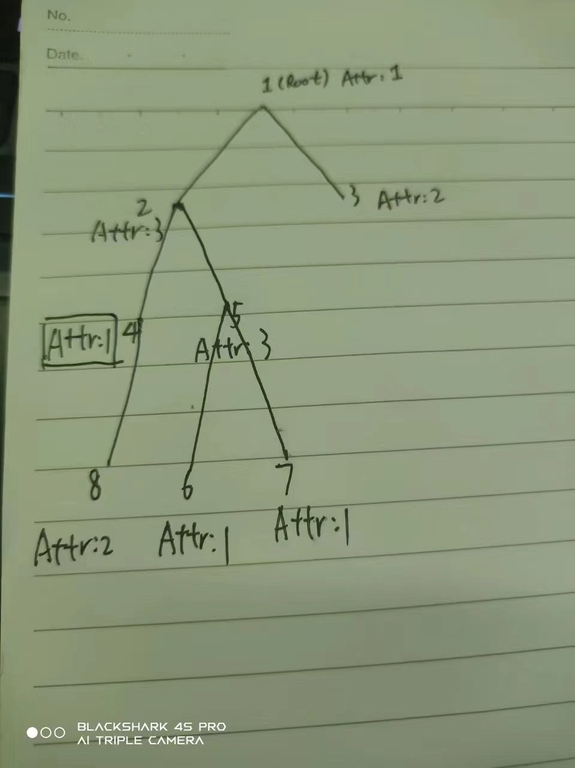
For example, if you delete the first edge $$$1-2$$$, Alice will win if she chooses to start at $$$8$$$.
If you delete the fourth edge $$$2-5$$$, Alice will win if she chooses to start at $$$6$$$ or $$$7$$$.
If you delete the second edge $$$1-3$$$, Bob will win. For example, if Alice choose to start at $$$7$$$, she will jump to $$$5$$$ and Bob jumps to $$$1$$$.
Notes:
(1) Constraint: $$$2 \leq n \leq 10^5$$$.
(2) There are $$$n-1$$$ queries and the deletion operations in queries are independent.
(3) Alice can only choose the original leaves of $$$T$$$ as the start vertex. Deleting an edge will result in more leaves, for example, if you delete $$$4-8$$$ in the second test case, $$$4$$$ becomes a new leaf but Alice cannot start from it.
(4) Neither Alice nor Bob can move across the root $$$1$$$. For example in the first test case, Alice cannot moves from $$$2$$$ to $$$3$$$ along $$$2-1-3$$$.






