I was using the Berlekamp-Massey (BM) algo for yesterday's H, but my sol worked too slow. Here is my idea:
(1) Divide $$$[1, n]$$$ into scales. Let $$$S(scale)$$$ be the scale $$$scale$$$, which is $$$S(scale)$$$ is $$$\{x | x \times scale \geq n, x \times scale/2 < n\}$$$. For example, if $$$n=7$$$, scale $$$1$$$ is $$$[7, 7]$$$, scale $$$2$$$ is $$$[3, 6]$$$, scale $$$4$$$ is $$$[2, 2]$$$, scale $$$8$$$ is $$$[1, 1]$$$. It is guaranteed that $$$scale$$$ is a power of $$$2$$$ in my sol.
(2)Fetch $$$O(log scale)$$$ consecutive items for each scale using the matrix fast power algorithm. The matrix is constructed in step (3) from the last scale.
(3)Using the BM algorithm to build a recurrence of length $$$O(log\,scale)$$$ and a recurrence matrix $$$M \in \mathbb{Z}/p\mathbb{Z}^{O(log\,scale) \times O(log\,scale)}$$$.
I mean for each scale we fetch some items $$$I$$$, get a recurrence using the BM algorithm, and construct a recurrence matrix $$$M$$$ using that recurrence, for example $$$a_r = a_{r+1} + a_{r+2}$$$, then
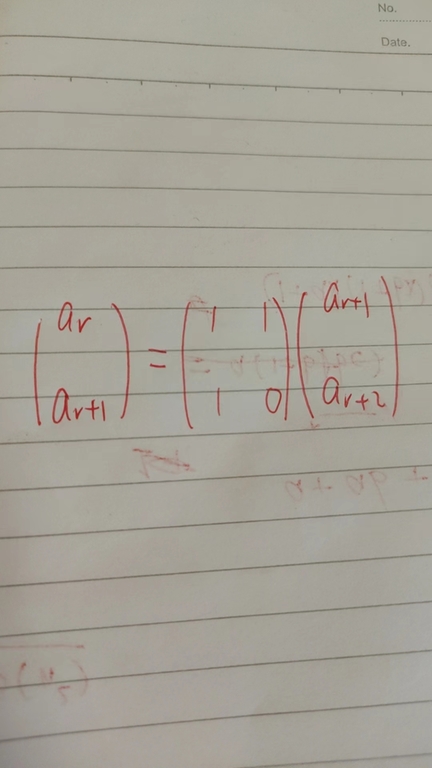
The matrix $$$M$$$ and the items $$$I$$$, and the fast matrix power algorithm, are used to fetching items for the next scale. This is a coarse-to-fine algorithm. The problem is that, for each scale, I need to fetch $$$O(log\,scale)$$$ items and each item costs $$$O(log\,scale^3log\,n)$$$ using a fast matrix power algorithm (matrix multiplication is $$$O(log\,scale^3)$$$, and there are up to $$$O(n)$$$ elements for each scale. Therefore the complexity for each scale is $$$O(log\,scale ^ 5 log\,n)$$$ and the overall complexity is $$$\sum\limits_{scale} O(log\,scale ^ 5 log\,n) = O((logn)^6)$$$ for each test case which is too slow. Any idea to speed up?
Code:
#define ATCODER 0
#include <bits/stdc++.h>
#if ATCODER
#include <atcoder/all>
using namespace atcoder;
#endif
using namespace std;
#pragma GCC optimize("Ofast,unroll-loops")
#pragma GCC target("avx2,tune=native")
#define ull unsigned long long
#define lp (p << 1)
#define rp ((p << 1)|1)
#define ll long long
#define ld long double
#define pb push_back
#define all(s) s.begin(), s.end()
#define sz(x) (int)(x).size()
#define fastio cin.tie(0) -> sync_with_stdio(0)
#define pii pair<int, int>
#define pil pair<int, ll>
#define pli pair<ll, int>
#define pll pair<ll, ll>
#define F(i, a, b) for(int i=(a); i <= (b); ++i)
#define SUM 0
#define MAX 1
#define fi first
#define se second
#define il inline
#define YES cout << "YES\n"
#define Yes cout << "Yes\n"
#define NO cout << "NO\n"
#define No cout << "No\n"
#define cans cout << ans << "\n"
#define PQ(TYPE, FUNCTOR) priority_queue<TYPE, vector<TYPE>, FUNCTOR<TYPE>>
#define HERE printf("HERE, __LINE__==%d\n", __LINE__);
#define INF 0x3f3f3f3f
#define INFLL 0x3f3f3f3f3f3f3f3fll
#define ld long double
#define fl std::cout << setprecision(15) << fixed
#define BT(x, i) (((x) & (1 << (i))) >> (i))
#define BTLL(x, i) (((x) & (1ll << (i))) >> (i))
const ld pi = acosl(-1);
long long power(long long a, long long b, int mod)
{
long long res=1;
while(b>0)
{
//a=a%mod;(有时候n的值太大了会超出long long的储存,所以要先取余)
if(b&1)//&位运算:判断二进制最后一位是0还是1,&的运算规则为前后都是1的时候才是1;
res=res*a%mod;
b=b>>1;//相当于除以2;
a=a*a%mod;
}
return res;
}
template<typename T, T...>
struct myinteger_sequence { };
template<typename T, typename S1 = void, typename S2 = void>
struct helper{
std::string operator()(const T& s){
return std::string(s);
}
};
template<typename T>
struct helper<T, decltype((void)std::to_string(std::declval<T>())), typename std::enable_if<!std::is_same<typename std::decay<T>::type, char>::value, void>::type>{
std::string operator()(const T& s){
return std::to_string(s);
}
};
template<typename T>
struct helper<T, void, typename std::enable_if<std::is_same<typename std::decay<T>::type, char>::value, void>::type>{
std::string operator()(const T& s){
return std::string(1, s);
}
};
template<typename T, typename S1 =void, typename S2 =void>
struct seqhelper{
const static bool seq = false;
};
template<typename T>
struct seqhelper<T, decltype((void)(std::declval<T>().begin())), decltype((void)(std::declval<T>().end()))>{
const static bool seq = !(std::is_same<typename std::decay<T>::type, std::string>::value);
};
template<std::size_t N, std::size_t... I>
struct gen_indices : gen_indices<(N - 1), (N - 1), I...> { };
template<std::size_t... I>
struct gen_indices<0, I...> : myinteger_sequence<std::size_t, I...> { };
template<typename T, typename REDUNDANT = void>
struct converter{
template<typename H>
std::string& to_string_impl(std::string& s, H&& h)
{
using std::to_string;
s += converter<H>().convert(std::forward<H>(h));
return s;
}
template<typename H, typename... T1>
std::string& to_string_impl(std::string& s, H&& h, T1&&... t)
{
using std::to_string;
s += converter<H>().convert(std::forward<H>(h)) + ", ";
return to_string_impl(s, std::forward<T1>(t)...);
}
template<typename... T1, std::size_t... I>
std::string mystring(const std::tuple<T1...>& tup, myinteger_sequence<std::size_t, I...>)
{
std::string result;
int ctx[] = { (to_string_impl(result, std::get<I>(tup)...), 0), 0 };
(void)ctx;
return result;
}
template<typename... S>
std::string mystring(const std::tuple<S...>& tup)
{
return mystring(tup, gen_indices<sizeof...(S)>{});
}
template<typename S=T>
std::string convert(const S& x){
return helper<S>()(x);
}
template<typename... S>
std::string convert(const std::tuple<S...>& tup){
std::string res = std::move(mystring(tup));
res = "{" + res + "}";
return res;
}
template<typename S1, typename S2>
std::string convert(const std::pair<S1, S2>& x){
return "{" + converter<S1>().convert(x.first) + ", " + converter<S2>().convert(x.second) + "}";
}
};
template<typename T>
struct converter<T, typename std::enable_if<seqhelper<T>::seq, void>::type>{
template<typename S=T>
std::string convert(const S& x){
int len = 0;
std::string ans = "{";
for(auto it = x.begin(); it != x.end(); ++it){
ans += std::move(converter<typename S::value_type>().convert(*it)) + ", ";
++len;
}
if(len == 0) return "{[EMPTY]}";
ans.pop_back(), ans.pop_back();
return ans + "}";
}
};
template<typename T>
std::string luangao(const T& x){
return converter<T>().convert(x);
}
static std::random_device rd; // random device engine, usually based on /dev/random on UNIX-like systems
// initialize Mersennes' twister using rd to generate the seed
static std::mt19937_64 rng{rd()};
//jiangly Codeforces
int P = 998244353;
using i64 = long long;
// assume -P <= x < 2P
int norm(int x) {
if (x < 0) {
x += P;
}
if (x >= P) {
x -= P;
}
return x;
}
template<class T>
T power(T a, i64 b) {
T res = 1;
for (; b; b /= 2, a *= a) {
if (b % 2) {
res *= a;
}
}
return res;
}
struct Z {
int x;
Z(int x = 0) : x(norm(x)) {}
Z(i64 x) : x(norm((int)(x % P))) {}
int val() const {
return x;
}
Z operator-() const {
return Z(norm(P - x));
}
Z inv() const {
assert(x != 0);
return power(*this, P - 2);
}
Z &operator*=(const Z &rhs) {
x = i64(x) * rhs.x % P;
return *this;
}
Z &operator+=(const Z &rhs) {
x = norm(x + rhs.x);
return *this;
}
Z &operator-=(const Z &rhs) {
x = norm(x - rhs.x);
return *this;
}
Z &operator/=(const Z &rhs) {
return *this *= rhs.inv();
}
friend Z operator*(const Z &lhs, const Z &rhs) {
Z res = lhs;
res *= rhs;
return res;
}
friend Z operator+(const Z &lhs, const Z &rhs) {
Z res = lhs;
res += rhs;
return res;
}
friend Z operator-(const Z &lhs, const Z &rhs) {
Z res = lhs;
res -= rhs;
return res;
}
friend Z operator/(const Z &lhs, const Z &rhs) {
Z res = lhs;
res /= rhs;
return res;
}
friend std::istream &operator>>(std::istream &is, Z &a) {
i64 v;
is >> v;
a = Z(v);
return is;
}
friend std::ostream &operator<<(std::ostream &os, const Z &a) {
return os << a.val();
}
};
template<typename T>
T exgcd(T &x, T &y, T a, T b)
{
if(!b)
{
x=1;
y=0;
return a;
}
exgcd(x,y,b,a%b);
T t=x;
x=y;
y=t-a/b*y;
return x*a+y*b;
}
#define MAXN 200005
// stores smallest prime factor for every number
int spf[MAXN];
bool notprime[MAXN];
int prime[MAXN], miu[MAXN], ptot;
int phi[MAXN];
// Calculating SPF (Smallest Prime Factor) for every
// number till MAXN.
// Time Complexity : O(nloglogn)
void sieve()
{
spf[1] = 1;
for (int i=2; i<MAXN; i++)
// marking smallest prime factor for every
// number to be itself.
spf[i] = i;
// separately marking spf for every even
// number as 2
for (int i=4; i<MAXN; i+=2)
spf[i] = 2;
for (int i=3; i*i<MAXN; i++)
{
// checking if i is prime
if (spf[i] == i)
{
// marking SPF for all numbers divisible by i
for (int j=i*i; j<MAXN; j+=i)
// marking spf[j] if it is not
// previously marked
if (spf[j]==j)
spf[j] = i;
}
}
}
void getmiu()
{
memset(notprime, 0, sizeof(notprime));
miu[1] = 1;
ptot = 0;
miu[1] = 1;
for(int i = 2; i < MAXN; i++) {
if(!notprime[i]) {
prime[ptot++] = i;
miu[i] = -1;
}
for(int j = 0; j < ptot && prime[j] * i < MAXN; j++) {
int k = prime[j] * i;
notprime[k] = true;
if(i % prime[j] == 0) {
miu[k] = 0; break;
} else {
miu[k] = -miu[i];
}
}
}
}
void getphi()
{
int n = MAXN - 1;
for (int i = 1; i <= n; i++)
phi[i] = i; // 除1外没有数的欧拉函数是本身,所以如果phi[i] = i则说明未被筛到
for (int i = 2; i <= n; i++)
if (phi[i] == i) // 未被筛到
for (int j = i; j <= n; j += i) // 所有含有该因子的数都进行一次操作
phi[j] = phi[j] / i * (i - 1);
}
template<typename T>
void facsieve(T x, map<T, T>& f)
{
while (x != 1)
{
f[spf[x]]++;
x = x / spf[x];
}
}
template<typename T>
void facnaive(T x, map<T, T>& f){
for (T p = 2; p * p <= x; ++p) {
if (x % p == 0) {
T k = 1;
for (x /= p; x % p == 0; x /= p) ++k;
f[p]+=k;
}
}
if (x > 1) f[x]++;
}
ll intsqrt (ll x) {
ll ans = 0;
for (ll k = 1LL << 30; k != 0; k /= 2) {
if ((ans + k) * (ans + k) <= x) {
ans += k;
}
}
return ans;
}
ll safelog(ll x){
for(ll i = 63; i >= 0; --i){
if(BTLL(x, i)) return i;
}
return -1;
}
template<typename T>
struct perf{
uint64_t t1, t2;
std::string hintline="";
bool verbose;
bool is_run;
perf():verbose(true), is_run(true){
t1 = (uint64_t)std::chrono::time_point_cast<T>(std::chrono::system_clock::now()).time_since_epoch().count();
}
perf(std::string hintline):hintline(hintline), verbose(true), is_run(true){
t1 = (uint64_t)std::chrono::time_point_cast<T>(std::chrono::system_clock::now()).time_since_epoch().count();
}
~perf(){
if(!is_run) return;
t2 = (uint64_t)std::chrono::time_point_cast<T>(std::chrono::system_clock::now()).time_since_epoch().count();
if(verbose)
std::cout << hintline << ": current:" << t2 - t1 << "\n";
is_run = false;
}
};
using perfm = perf<std::chrono::microseconds>;
template<typename S>
struct shash{
const S& t;
int radix, base;
std::vector<int> primes;
constexpr std::pair<long long, long long> inv_gcd(long long a, long long b) {
a = safe_mod(a, b);
if (a == 0) return {b, 0};
// Contracts:
// [1] s - m0 * a = 0 (mod b)
// [2] t - m1 * a = 0 (mod b)
// [3] s * |m1| + t * |m0| <= b
long long s = b, t = a;
long long m0 = 0, m1 = 1;
while (t) {
long long u = s / t;
s -= t * u;
m0 -= m1 * u; // |m1 * u| <= |m1| * s <= b
// [3]:
// (s - t * u) * |m1| + t * |m0 - m1 * u|
// <= s * |m1| - t * u * |m1| + t * (|m0| + |m1| * u)
// = s * |m1| + t * |m0| <= b
auto tmp = s;
s = t;
t = tmp;
tmp = m0;
m0 = m1;
m1 = tmp;
}
// by [3]: |m0| <= b/g
// by g != b: |m0| < b/g
if (m0 < 0) m0 += b / s;
return {s, m0};
}
constexpr long long safe_mod(long long x, long long m) {
x %= m;
if (x < 0) x += m;
return x;
}
struct barrett {
unsigned int _m;
unsigned long long im;
// @param m `1 <= m < 2^31`
barrett(){}
void set(unsigned int m){
_m = m;
im = (unsigned long long)(-1) / m + 1;
}
explicit barrett(unsigned int m) : _m(m), im((unsigned long long)(-1) / m + 1) {}
// @return m
unsigned int umod() const { return _m; }
// @param a `0 <= a < m`
// @param b `0 <= b < m`
// @return `a * b % m`
unsigned int mul(unsigned int a, unsigned int b) const {
// [1] m = 1
// a = b = im = 0, so okay
// [2] m >= 2
// im = ceil(2^64 / m)
// -> im * m = 2^64 + r (0 <= r < m)
// let z = a*b = c*m + d (0 <= c, d < m)
// a*b * im = (c*m + d) * im = c*(im*m) + d*im = c*2^64 + c*r + d*im
// c*r + d*im < m * m + m * im < m * m + 2^64 + m <= 2^64 + m * (m + 1) < 2^64 * 2
// ((ab * im) >> 64) == c or c + 1
unsigned long long z = a;
z *= b;
#ifdef _MSC_VER
unsigned long long x;
_umul128(z, im, &x);
#else
unsigned long long x =
(unsigned long long)(((unsigned __int128)(z)*im) >> 64);
#endif
unsigned int v = (unsigned int)(z - x * _m);
if (_m <= v) v += _m;
return v;
}
};
struct dynamic_modint {
using mint = dynamic_modint;
int mod() { return (int)(bt.umod()); }
static mint raw(int v) {
mint x;
x._v = v;
return x;
}
dynamic_modint() : _v(0) {}
template<typename T>
dynamic_modint(T v, int m) {
bt.set(m);
long long x = (long long)(v % (long long)(mod()));
if (x < 0) x += mod();
_v = (unsigned int)(x);
}
unsigned int val() const { return _v; }
mint& operator++() {
_v++;
if (_v == umod()) _v = 0;
return *this;
}
mint& operator--() {
if (_v == 0) _v = umod();
_v--;
return *this;
}
mint operator++(int) {
mint result = *this;
++*this;
return result;
}
mint operator--(int) {
mint result = *this;
--*this;
return result;
}
mint& operator+=(const mint& rhs) {
_v += rhs._v;
if (_v >= umod()) _v -= umod();
return *this;
}
mint& operator-=(const mint& rhs) {
_v += mod() - rhs._v;
if (_v >= umod()) _v -= umod();
return *this;
}
mint& operator*=(const mint& rhs) {
_v = bt.mul(_v, rhs._v);
return *this;
}
mint& operator/=(const mint& rhs) { return *this = *this * rhs.inv(); }
mint operator+() const { return *this; }
mint operator-() const { return mint() - *this; }
mint pow(long long n) const {
assert(0 <= n);
mint x = *this, r = 1;
while (n) {
if (n & 1) r *= x;
x *= x;
n >>= 1;
}
return r;
}
mint inv() const {
auto eg = inv_gcd(_v, mod());
assert(eg.first == 1);
return eg.second;
}
friend mint operator+(const mint& lhs, const mint& rhs) {
return mint(lhs) += rhs;
}
friend mint operator-(const mint& lhs, const mint& rhs) {
return mint(lhs) -= rhs;
}
friend mint operator*(const mint& lhs, const mint& rhs) {
return mint(lhs) *= rhs;
}
friend mint operator/(const mint& lhs, const mint& rhs) {
return mint(lhs) /= rhs;
}
friend bool operator==(const mint& lhs, const mint& rhs) {
return lhs._v == rhs._v;
}
friend bool operator!=(const mint& lhs, const mint& rhs) {
return lhs._v != rhs._v;
}
private:
unsigned int _v;
barrett bt;
unsigned int umod() { return bt.umod(); }
};
std::map<int, std::vector<dynamic_modint>> f; //不同素数的前缀和
std::map<int, std::vector<dynamic_modint>> radixmap;
shash()=delete;
shash(const S& t, int radix=27, int base=(int)'a'-1, std::vector<int> primes={998244353, 1000000007}):t(t), radix(radix), base(base), primes(primes){
for(int p: primes){
f[p].resize(t.size());
radixmap[p].resize(t.size());
f[p][0] = dynamic_modint(0, p);
dynamic_modint tmp(radix, p);
radixmap[p][0] = dynamic_modint(1, p);
for(int i = 1; i < t.size(); ++i){
f[p][i] = f[p][i-1]*tmp + dynamic_modint(t[i] - base, p);
radixmap[p][i] = radixmap[p][i-1] * tmp;
}
}
}
std::map<int, dynamic_modint> operator()(const int l, const int r){
std::map<int, dynamic_modint> res;
if(l > r) return res;
for(int p: primes){
res[p] = f[p][r] - f[p][l-1]*radixmap[p][r-l+1];
}
return res;
}
std::map<int, dynamic_modint> operator()(){
return this->operator()(1, (int)t.size()-1);
}
std::map<int, dynamic_modint> operator()(const std::vector<std::pair<int, int>>& prs){
std::map<int, dynamic_modint> res;
for(int p: primes){
res[p] = dynamic_modint(0, p);
}
for(const auto& [l, r]: prs){
std::map<int, dynamic_modint> res2 = this->operator()(l, r);
if(res2.empty()){
continue;
}else{
for(int p: primes){
res[p] = res[p]*radixmap[p][r-l+1] + res2[p];
}
}
}
return res;
}
};
struct dsu{
int n;
int *pa, *dsusz;
dsu(int n): n(n){
pa = new int[n+1];
dsusz = new int[n+1];
reset();
}
int find(int x){
if(pa[x] == x) return x;
pa[x] = find(pa[x]);
return pa[x];
}
int un(int x, int y, int swapsz=1){
int fx = find(x), fy = find(y);
if(fx == fy) return -1;
if(dsusz[fx] > dsusz[fy] && swapsz) swap(fx, fy);
pa[fx] = fy;
dsusz[fy] += dsusz[fx];
dsusz[fx] = 0;
return fy;
}
int comp(){
int st = 0;
for(int i = 1; i <= n; ++i){
if(pa[i] == i){
++st;
}
}
return st;
}
void reset(){
for(int i = 1; i <= n; ++i){
pa[i] = i;
dsusz[i] = 1;
}
}
~dsu(){
delete[] pa;
delete[] dsusz;
}
};
template<typename T=int, typename S=T>
struct BIT{
bool usep;
int n, digits;
T* p; //元素类型
S* q; //数组类型
template<typename SIGNED>
SIGNED lowbit(SIGNED x){
return x & (-x);
}
BIT(int n, T* p=nullptr):n(n), digits(0), p(p){
usep = (p != nullptr);
q = new S[n+1];
memset(q, 0, (n+1)*sizeof(S));
getdigits();
if(usep) init();
}
void init(){
//O(n)时间内建树
for(int i = 1; i <= n; ++i){
q[i] += (S)p[i];
int j = i + lowbit(i);
if(j <= n) {
q[j] += q[i];
}
}
}
void add(int x, int k){
while(x <= n && x >= 1){
q[x] = q[x] + (S)k;
x += lowbit(x);
}
}
S getsum(int x){
S ans = 0;
while(x >= 1){
ans += q[x];
x -= lowbit(x);
}
return ans;
}
void getdigits(){
if(digits) return;
int tmp = n;
while(tmp){
tmp >>= 1;
digits++;
}
}
int search(S target){
//最长前缀和
int t = 0;
S s = 0;
for(int i = digits-1; i >= 0; --i){
if((t + (1 << i) <= n) && (s + q[t + (1<<i)] <= target)){
s += q[t + (1<<i)];
t += (1 << i);
}
}
return t;
}
int binsearch(S target){
int l = 1, r = n, ans = 0;
while(l <= r){
int mid = (l + r)/2;
if(getsum(mid) == target){
ans = mid;
l = mid + 1;
}else if(getsum(mid) < target){
l = mid + 1;
}else{
r = mid - 1;
}
}
return ans;
}
~BIT(){
delete[] q;
}
};
vector<int> digits(ll x){
stack<int> st;
while(x){
st.push(x%10);
x/=10;
}
vector<int> res;
while(!st.empty()){
res.push_back(st.top());
st.pop();
}
return res;
}
bool isprime(int x){
if(x <= 3) return (x!=1);
for(int i = 2; i * i <= x; ++i){
if(x%i == 0){
return false;
}
}
return true;
}
struct Comb {
int n;
std::vector<Z> _fac;
std::vector<Z> _invfac;
std::vector<Z> _inv;
Comb() : n{0}, _fac{1}, _invfac{1}, _inv{0} {}
Comb(int n) : Comb() {
init(n);
}
void init(int m) {
if (m <= n) return;
_fac.resize(m + 1);
_invfac.resize(m + 1);
_inv.resize(m + 1);
for (int i = n + 1; i <= m; i++) {
_fac[i] = _fac[i - 1] * i;
}
_invfac[m] = _fac[m].inv();
for (int i = m; i > n; i--) {
_invfac[i - 1] = _invfac[i] * i;
_inv[i] = _invfac[i] * _fac[i - 1];
}
n = m;
}
Z fac(int m) {
if (m > n) init(2 * m);
return _fac[m];
}
Z invfac(int m) {
if (m > n) init(2 * m);
return _invfac[m];
}
Z inv(int m) {
if (m > n) init(2 * m);
return _inv[m];
}
Z binom(int n, int m) {
if (n < m || m < 0) return 0;
return fac(n) * invfac(m) * invfac(n - m);
}
} comb;
namespace atcoder {
namespace internal {
template <class E> struct csr {
std::vector<int> start;
std::vector<E> elist;
explicit csr(int n, const std::vector<std::pair<int, E>>& edges)
: start(n + 1), elist(edges.size()) {
for (auto e : edges) {
start[e.first + 1]++;
}
for (int i = 1; i <= n; i++) {
start[i] += start[i - 1];
}
auto counter = start;
for (auto e : edges) {
elist[counter[e.first]++] = e.second;
}
}
};
// Reference:
// R. Tarjan,
// Depth-First Search and Linear Graph Algorithms
struct scc_graph {
public:
explicit scc_graph(int n) : _n(n) {}
int num_vertices() { return _n; }
void add_edge(int from, int to) { edges.push_back({from, {to}}); }
// @return pair of (# of scc, scc id)
std::pair<int, std::vector<int>> scc_ids() {
auto g = csr<edge>(_n, edges);
int now_ord = 0, group_num = 0;
std::vector<int> visited, low(_n), ord(_n, -1), ids(_n);
visited.reserve(_n);
auto dfs = [&](auto self, int v) -> void {
low[v] = ord[v] = now_ord++;
visited.push_back(v);
for (int i = g.start[v]; i < g.start[v + 1]; i++) {
auto to = g.elist[i].to;
if (ord[to] == -1) {
self(self, to);
low[v] = std::min(low[v], low[to]);
} else {
low[v] = std::min(low[v], ord[to]);
}
}
if (low[v] == ord[v]) {
while (true) {
int u = visited.back();
visited.pop_back();
ord[u] = _n;
ids[u] = group_num;
if (u == v) break;
}
group_num++;
}
};
for (int i = 0; i < _n; i++) {
if (ord[i] == -1) dfs(dfs, i);
}
for (auto& x : ids) {
x = group_num - 1 - x;
}
return {group_num, ids};
}
std::vector<std::vector<int>> scc() {
auto ids = scc_ids();
int group_num = ids.first;
std::vector<int> counts(group_num);
for (auto x : ids.second) counts[x]++;
std::vector<std::vector<int>> groups(ids.first);
for (int i = 0; i < group_num; i++) {
groups[i].reserve(counts[i]);
}
for (int i = 0; i < _n; i++) {
groups[ids.second[i]].push_back(i);
}
return groups;
}
private:
int _n;
struct edge {
int to;
};
std::vector<std::pair<int, edge>> edges;
};
} // namespace internal
struct scc_graph {
public:
scc_graph() : internal(0) {}
explicit scc_graph(int n) : internal(n) {}
void add_edge(int from, int to) {
int n = internal.num_vertices();
assert(0 <= from && from < n);
assert(0 <= to && to < n);
internal.add_edge(from, to);
}
std::vector<std::vector<int>> scc() { return internal.scc(); }
private:
internal::scc_graph internal;
};
} // namespace atcoder
#define DEBUG 1
#define SINGLE 0
#define cstr(x) (luangao(x).c_str())
void debug(const char* p){
#if DEBUG
freopen(p, "r", stdin);
#else
fastio;
#endif
}
constexpr int p = 998244353;
#define cstr(x) (luangao(x).c_str())
vector<int> berlekamp_massey(vector<int> a, int p) {
for(int& x: a){
if(x < 0) x%=p, x+=p;
}
vector<int> v, last; // v is the answer, 0-based, p is the module
int k = -1, delta = 0;
for (int i = 0; i < (int)a.size(); i++) {
int tmp = 0;
for (int j = 0; j < (int)v.size(); j++)
tmp = (tmp + (long long)a[i - j - 1] * v[j]) % p;
if (a[i] == tmp) continue;
if (k < 0) {
k = i;
delta = (a[i] - tmp + p) % p;
v = vector<int>(i + 1);
continue;
}
vector<int> u = v;
int val = (long long)(a[i] - tmp + p) * power(delta, p - 2, p) % p;
if (v.size() < last.size() + i - k) v.resize(last.size() + i - k);
(v[i - k - 1] += val) %= p;
for (int j = 0; j < (int)last.size(); j++) {
v[i - k + j] = (v[i - k + j] - (long long)val * last[j]) % p;
if (v[i - k + j] < 0) v[i - k + j] += p;
}
if ((int)u.size() - i < (int)last.size() - k) {
last = u;
k = i;
delta = a[i] - tmp;
if (delta < 0) delta += p;
}
}
for (auto &x : v) x = (p - x) % p;
v.insert(v.begin(), 1);
return v; // $$$\forall i, \sum_{j = 0} ^ m a_{i - j} v_j = 0$$$
}
vector<vector<Z>> getmatrix(vector<int>& bm){
vector<vector<Z>> res;
int m = (int)bm.size()-1;
res.resize(m+1);
F(i, 0, m) res[i].resize(m+1);
F(i, 1, m){
F(j, 1, m){
if(i == 1){
res[i][j] = -Z(bm[j]);
}
else{
res[i][j] = (i - j == 1);
}
}
}
return res;
}
vector<vector<Z>> matmul(vector<vector<Z>>& a, vector<vector<Z>>& b){
int m = a.size()-1;
vector<vector<Z>> res(m+1, vector<Z>(m+1));
F(i, 1, m){
F(j, 1, m){
F(k, 1, m){
res[i][j] += a[i][k] * b[k][j];
}
}
}
return res;
}
vector<vector<Z>> fp(vector<vector<Z>>& bm, ll x){
int m = bm.size()-1;
if(x == 0){
vector<vector<Z>> res(m+1, vector<Z>(m+1));
F(i, 1, m){
F(j, 1, m){
res[i][j] = (i == j);
}
}
return res;
}else if(x == 1) return bm;
auto tmp = fp(bm, x/2);
auto res = matmul(tmp, tmp);
if(x%2){
res = matmul(res, bm);
}
return res;
}
void solve(int test){
ll n;
cin >> n;
ll scale = 1; //处理x * scale >= n的区间
vector<vector<Z>> lastbm;
vector<Z> lastres, lastres2;
auto getlbub = [&](ll scale) -> pll{
return {(n + scale - 1)/scale, (scale == 1 ? n : ((n + scale/2 - 1)/(scale/2) - 1))};
};
function<Z(ll)> getans = [&](ll x) -> Z{
if(x >= n) return 0;
if(scale/2 * x >= n){
//assert(lastres.size()+1 == lastbm.size());
//属于上一个scale
auto [lastlb, lastub] = getlbub(scale/2);
int m = (int)lastbm.size()-1;
ll diff = lastub - x;
if(diff < lastres.size()){
//printf("[1]scale==%lld, x==%lld, diff==%lld, ans==%d, lastres.size()==%zu, lastbm.size()==%zu\n", scale, x, diff, lastres[diff].val(), lastres.size(), \
lastbm.size());
return lastres[diff];
}
ll times = diff - m + 1;
auto fpres = fp(lastbm, times);
//printf("lastres.size()==%zu, m==%d\n", lastres.size(), m);
Z ans = 0;
for(int i = 1; i <= m; ++i){
ans += fpres[1][i] * lastres[m - i];
}
//printf("[2]scale==%lld, x==%lld, ans==%lld\n", scale, x, ans);
return ans;
}
return 1 + getans(x+1)/2 + getans(2*x)/2;
};
ll scaletimes = 0;
while(scale <= n){
auto [lb, ub] = getlbub(scale);
lastres2.clear();
vector<int> trial;
vector<int> lastbmres;
ll x = ub;
for(; x >= max(lb, ub-3*scaletimes); --x){
Z res = getans(x);
trial.pb(res.val());
lastres2.pb(res);
}
lastbmres = berlekamp_massey(trial, P);
//printf("scale==%lld, x==%lld, lastbmres==%d\n", scale, x, (int)lastbmres.size());
printf("scale==%lld[%lld, %lld], trial==%s, lastbmres==%s\n", scale, lb, ub, cstr(trial), cstr(lastbmres));
lastres = lastres2;
lastbm = getmatrix(lastbmres);
scale *= 2;
++scaletimes;
}
Z ans = getans(1);
cans;
}
signed main(int argc, char** argv){
debug(argc==1?"test1.txt":argv[1]);
int t = 1;
int test = 1;
#if !SINGLE
cin >> t;
#endif
while(t--){
solve(test++);
}
}






