I was solving a problem Tree cutting (Easy version) and I used only dfs. But now I am wondering about the problem Tree cutting (Hard version). I stuck at some part which is an interesting problem itself.
(If you think that this problem can be solved then feel free to give your approach in comments).

First let me tell you my approach for Tree cutting (Hard version).
We need to group all the colours with smallest subtree. Then you will remain with some (let say m) black nodes subtree. Now think about this subtree is giving some answer ki. Then our final answer will be (k1*k2*k3...*km)%mod.

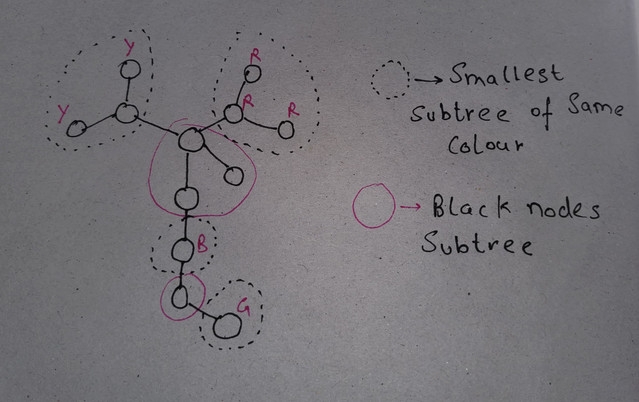
Now my question arises :

You are given a tree with some nodes are red coloured and other are black and each red node have some value ri>=1 (here red nodes are showing that this node is connected with ri coloured subtree in prev question). Now you need to find number of different ways of cutting this tree such that every subtree after cutting must have at least one red node. Let's say after cutting we have T different subtree, then the value of a subtree will be summation of all value of red nodes present in it (lets say this summation is ti).Then value of way of cutting is t1*t2*...*tT. We need to output the summation of result of all possible way of cutting.
constraints n <= 2*10^5;
The answer may be large, so print it modulo 998244353

Example:

number of nodes = n = 3
number of red nodes = r = 2
Given tree is
1 — 2
2 — 3
red nodes are 1,2 their values are 1,2 respectively.

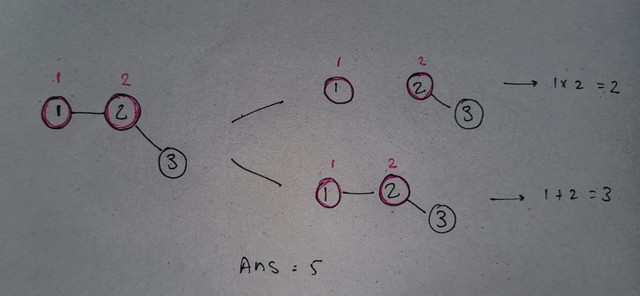
in this example we can cut this tree in 2 different ways
1st way(cut the edge between 1 — 2) the answer is 2 (multiplication of results of all subtree)
2nd way(don't cut any edge) the answer is 3 (summation of all value of red node in a subtree)
final answer = 3+2 = 5

I hope you are able to understand my problem. If you can find some answer then please share!