↵
**Нормали тетраэра**↵
↵
<spoiler summary="Условие">↵
В тетраэдре проведены внешние векторы нормалей ко всем граням. Длина каждого вектора численно равна площади соответствующей грани. Доказать, что сумма векторов равна 0↵
</spoiler>↵
↵
↵
<spoiler summary="Решение">↵
Закачаем в тетраэдр газ давления `p`. Тогда сила, с которой газ давит на грань, перпендикулярна грани и пропорциональна ее площади: `F = pS`. Из условия равновесия, сумма сил равна 0, и тогда сумма наших веркторов тоже равна 0. Это доказательство легко обобщается на произвольный многогранник.↵
</spoiler>↵
↵
**Теорема Пифагора**↵
↵
<spoiler summary="Условие">↵
Общеизвестно↵
</spoiler>↵
↵
↵
<spoiler summary="Решение">↵
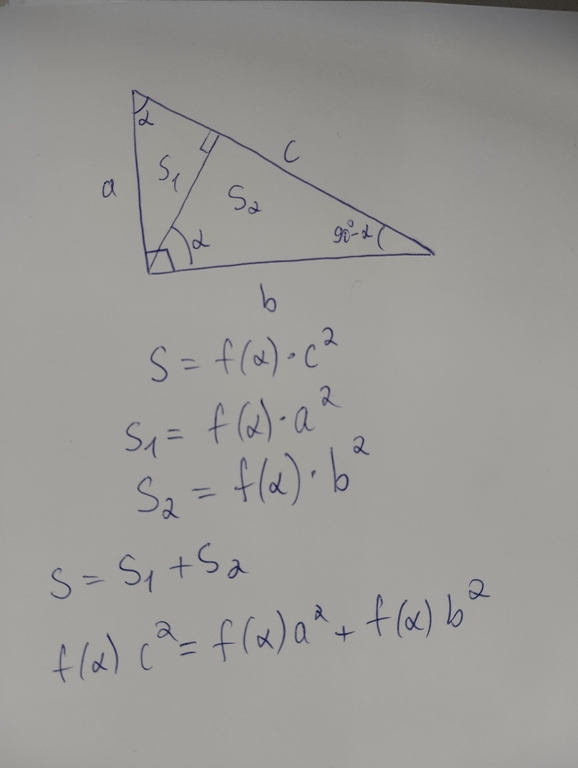↵
↵
Ясно, что прямоугольный треугольник определяется гипотенузой `c` и углом при вершине `α`. Тогда, из соображений размерности, его площадь `S` равна `f(α) * c^2`, где `f(x)` — какая-то функция от угла (на самом деле, `f(x) = 0.5 * sin(x)`). Проведём высоту к гипотенузе, разделив треугольник на два маленьких треугольника с площадями `S1` и `S2`. В обоих треугольниках есть угол `α`. Суммируя их площади по формуле, сокращаем на `f(α)` и получаем требуемое равенство.↵
</spoiler>↵
↵
**Точка Торричелли**↵
↵
<spoiler summary="Условие">↵
Внутри остроугольного треугольника ABC отмечена точка P, минимизирующая сумму расстояний PA+PB+PC. Доказать, что стороны треугольника видны из точки P под равными углами.↵
</spoiler>↵
↵
↵
<spoiler summary="Решение">↵
↵
↵
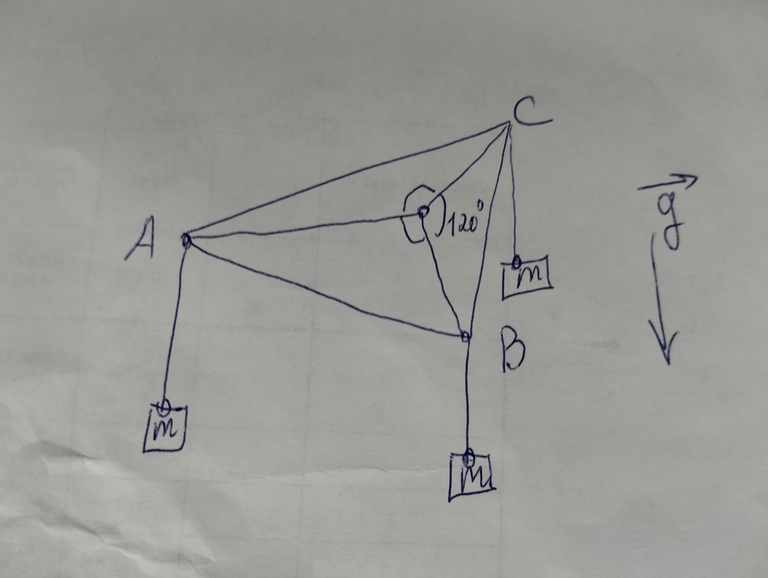
Скрепим три нити в одной точке (точке P), которая может свободно скользить по плоскости. Сделаем отверстия в вершинах треугольника и пропустим через них нити. Подвесим на нижние концы нитей грузы равной массы. Минимум потенциальной энергии соответствует максимальной суммарной длине вертикальных отрезков нитей, то есть минимальной суммарной длине отрезков PA, PB, PC. Точка P находится в покое, и на неё действуют три одинаковые силы. Тогда из симметрии углы между каждой парой нитей равны по 120 градусов
If you know any "proofs", you can share them. I also know some:↵
↵
**Tetrahedron normals**↵
↵
<spoiler summary="Statement">↵
In a tetrahedron, external normal vectors are drawn to all faces. The length of each vector is numerically equal to the area of the corresponding face. Prove that the sum of vectors is 0↵
</spoiler>↵
↵
↵
<spoiler summary="Solution">↵
Let us pump gas at pressure `p` into the tetrahedron. Then the force the gas pushes on the face is perpendicular to the face and proportional to its area: `F = pS`. From the equilibrium condition, the sum of the forces is 0, and then the sum of our verctors is also 0. This proof can easily be generalized to an arbitrary polyhedron.↵
</spoiler>↵
↵
**Pythagorean theorem**↵
↵
<spoiler summary="Statement">↵
Well-known↵
</spoiler>↵
↵
↵
<spoiler summary="Solution">↵
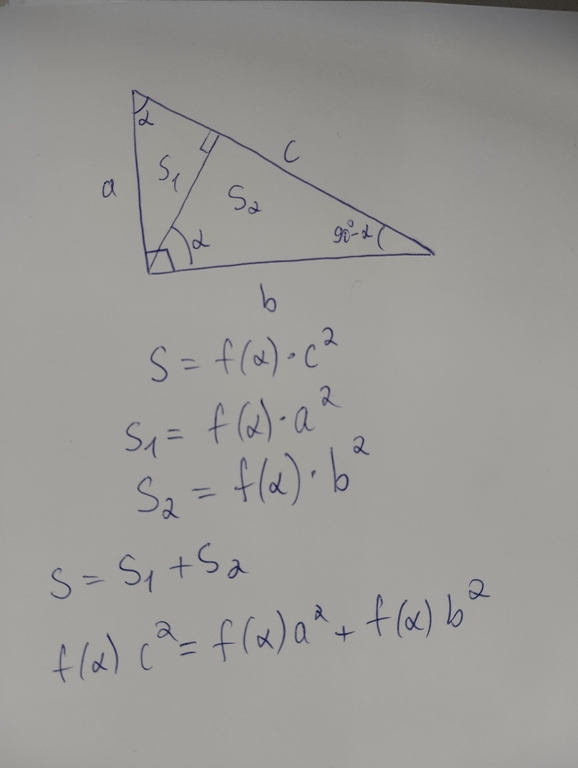↵
↵
A right triangle is defined by the hypotenuse `c` and the vertex angle `α`. Then, from dimensional considerations, its area `S` is equal to `f(α) * c^2`, where `f(x)` — some function of the angle (in fact, `f(x) = 0.5 * sin(x)`). Let's draw the height to the hypotenuse, dividing the triangle into two small triangles with areas `S1` and `S2`. Both triangles have an angle `α`. Summing up their areas using the formula, we reduce them by `f(α)` and get the equality.↵
</spoiler>↵
↵
**Точка Торричелли**↵
↵
<spoiler summary="Statement">↵
Inside an acute triangle ABC, a point P is marked, minimizing the sum of the distances PA+PB+PC. Prove that the sides of the triangle ABC are visible from point P at equal angles.↵
</spoiler>↵
↵
↵
<spoiler summary="Solution">↵
↵
↵
Let's fasten three threads at one point (point P), which can slide freely along the plane. Let's make holes in the vertices of the triangle and pass the threads through them. We attach 3 equal masses on the lower ends of the threads. The minimum potential energy corresponds to the maximum total length of the vertical segments of the threads, that is, the minimum total length of segments PA, PB, PC. Point P is in a state of equilibrium, and three identical forces pull it. Then, from symmetry, the angles between each pair of threads are equal to 120 degrees.↵
</spoiler>↵
↵






