↵
**Нормали тетраэра
If you know any "proofs", you can share them. I also know some:↵
↵
**Tetrahedron normals**↵
↵
<spoiler summary="
В тетраэдре проведены внешние векторы нормалей ко всем граням. Длина каждого вектора численно равна площади соответствующей грани. Доказать, что сумма векторов равна 0↵
</spoiler>↵
↵
↵
<spoiler summary="Решение">↵
Закачаем в тетраэдр газ давления `p`. Тогда сила, с которой газ давит на грань, перпендикулярна грани и пропорциональна ее площади: `F = pS`. Из условия равновесия, сумма сил равна 0, и тогда сумма наших веркторов тоже равна 0. Это доказательство легко обобщается на произвольный многогранник.↵
</spoiler>↵
↵
**Теорема Пифагора
In a tetrahedron, external normal vectors are drawn to all faces. The length of each vector is numerically equal to the area of the corresponding face. Prove that the sum of vectors is 0↵
</spoiler>↵
↵
↵
<spoiler summary="Solution">↵
Let us pump gas at pressure `p` into the tetrahedron. Then the force the gas pushes on the face is perpendicular to the face and proportional to its area: `F = pS`. From the equilibrium condition, the sum of the forces is 0, and then the sum of our verctors is also 0. This proof can easily be generalized to an arbitrary polyhedron.↵
</spoiler>↵
↵
**Pythagorean theorem**↵
↵
<spoiler summary="
Общеизвестно
Well-known↵
</spoiler>↵
↵
↵
<spoiler summary="
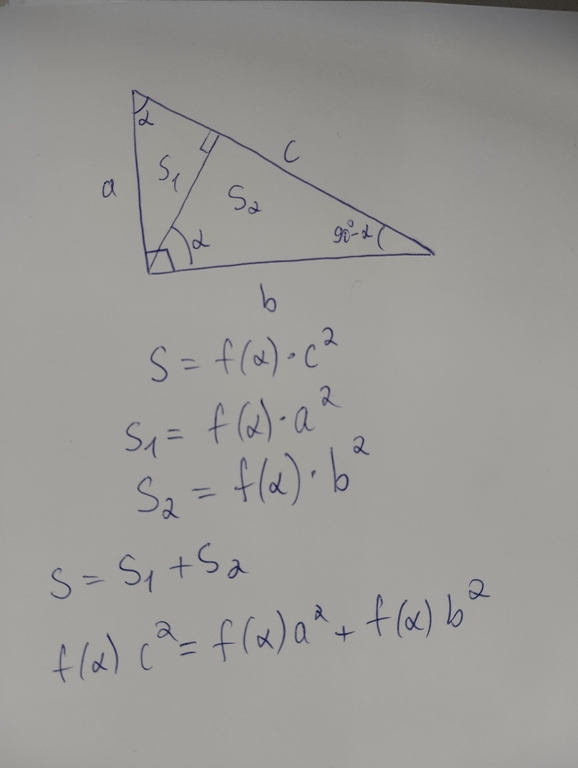↵
↵
</spoiler>↵
↵
**Точка Торричелли**↵
↵
<spoiler summary="
Внутри остроугольного треугольника ABC отмечена точка P, минимизирующая сумму расстояний PA+PB+PC. Доказать, что стороны треугольника видны из точки P под равными углами
Inside an acute triangle ABC, a point P is marked, minimizing the sum of the distances PA+PB+PC. Prove that the sides of the triangle ABC are visible from point P at equal angles.↵
</spoiler>↵
↵
↵
<spoiler summary="
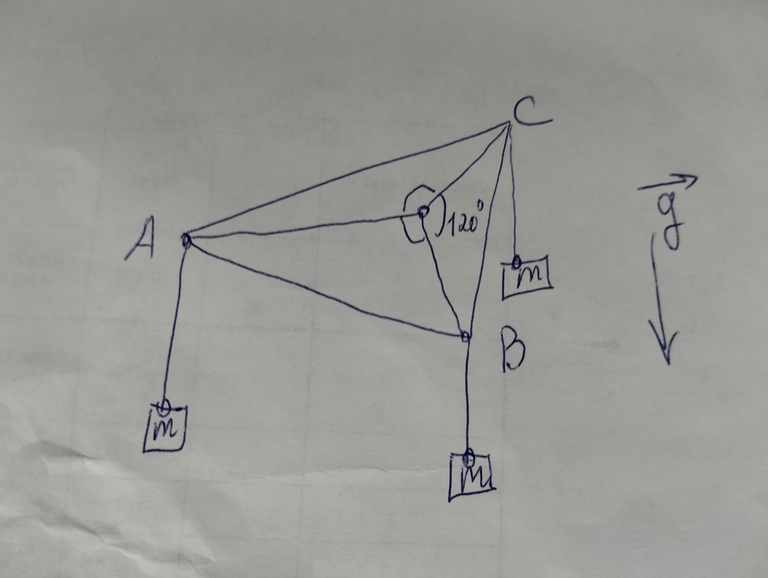↵
↵
</spoiler>↵
↵






