We can observe that "O" and "K" do not "interlock" with each other. So this problem is just finding two disjoint $$$4 \times 3$$$ sub-grids. Using brute force is enough.

Bonus: solve the problem when $$$n,m \le 10^3$$$.

#include <bits/stdc++.h>
using namespace std;
#define int long long

void solve() {
    int n, m; cin >> n >> m;
    int ans = 0;
    for (int i = 0; i < n-3; i++) {
        for (int j = 0; j < m-2; j++) {
            for (int i2 = 0; i2 < n-3; i2++) {
                for (int j2 = 0; j2 < m-2; j2++) {
                    if (min(i, i2) + 3 < max(i, i2) || min(j, j2) + 2 < max(j, j2)) {
                        ans++;
                    }
                }
            }
        }
    }
    cout << ans << "\n";
}

signed main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    //freopen("file.in", "r", stdin)
    //freopen("file.out", "w", stdout);
    int t;
    cin >> t;
    while (t--) solve();
    return 0;
}

Note $$$k$$$ is the maximum integer such that $$$2^k \le n$$$. We can proof $$$a+b \le 2^(k+1)-1$$$.

Proof:since $$$a$$$ & $$$b=0$$$, there is no carry bit in $$$a+b$$$. And we can pick $$$a=2^{k}-1$$$ and $$$b=2^{k}$$$ to make $$$a+b=2^(k+1)-1$$$.

When $$$a+b=2^(k+1)-1$$$, we can see picking $$$a=2^{k}-1$$$ and $$$b=2^{k}$$$ makes $$$a \cdot b$$$ maximum. So the answer is $$$2^{k} \cdot (2^{k}-1)$$$.

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define fast                       \
 ios_base::sync_with_stdio(0);      \
 cin.tie(0);                         \
 cout.tie(0);
 
int main(){
    fast;
    ll t;
    cin>>t;
    while(t--){
        ll n;
        cin>>n;
        ll val=0;
        for(ll i=0;i<31;i++){
            if((n&(1LL<<i))>0) val=i;
        }
        cout<<(1LL<<val)*((1LL<<val)-1)<<"\n";
    }
}

Note $$$k$$$ is the maximum integer such that $$$2^k \le n$$$. At first, we can easily see a lower bound of the answer — $$$2^{k-1}$$$. To reach this lower bound, we just pick $$$a=2^{k-1}$$$ and $$$b=2^k$$$.

Next, we only consider $$$a∈[2^{k-1}+1,2^{k}-1]$$$ and $$$b∈[2^k+1,2^k+2^{k-1}-1]$$$ which make $$$\gcd(a,b)>2^{k-1}$$$ possible.

We can see the following conclusions.

Conclution 1: $$$\gcd(a,b)=a$$$.

Proof 1: if $$$\gcd(a,b)<a$$$, it means $$$\gcd(a,b)\le a/2 <2^{k-1}$$$, which is too small.

Conclution 2: $$$b=2a$$$.

Proof 2: if $$$b=ka(k>2)$$$, it means $$$b>2^k+2^{k-1}$$$, which is too large.

Now, we need to find the maximum $$$a$$$ that satisfies $$$a$$$ & $$$2a=0$$$. This only holds when there are no two consecutive $$$1$$$'s in the binary representation of $$$a$$$. So, the answer is a number — the largest, not exceeding $$$n$$$, where there are no two consecutive $$$1$$$'s in binary representation.

#include <bits/stdc++.h>
#define all(s) s.begin(), s.end()

using namespace std;
using ll = long long;

const int _N = 1e5 + 5;

void solve() {
	ll n; cin >> n;
	ll x = 0;
	int lst = 0;
	for (ll bit = 29; bit >= 0; bit--) {
		if (x + (1 << bit) <= n && lst == 0) {
			lst = 1;
			x |= (1 << bit);
		} else lst = 0;
	}
	cout << x / 2 << '\n';
}

int main() {
	int T; cin >> T;
	while (T--) {
		solve();
	}
}

First, since $$$(a+b)^2 = a^2 + b^2 + 2ab > a^2+b^2$$$, it's obvious that sum up the numbers first will give a better answer.

Also if there's only one tuple left having positive value, choosing operation $$$1$$$ will give a better answer.

Therefore we will first sum up $$$max(a_i,b_i)$$$ for all tuples, then check $$$min(a_i,b_i)$$$ for all tuples for being the one to perform operation $$$1$$$ to, and find the best answer.

The time complexity will be $$$O(n\ log\ n)$$$ or $$$O(n)$$$ depends on your implementation.

#include<bits/stdc++.h>
#define pi 3.14159265358979323846
#define eb emplace_back
#define ll long long
#define w(t) while(t--)
#define F first
#define S second
#define pii pair<int,int>
#define pll pair<ll,ll>
#define iofast ios::sync_with_stdio(0);cin.tie(0);
using namespace std;
//give sin(),cos() radian, and asin(),acos() gives you radian
struct aaa{
	ll a,b;
}arr[200010];
void solve(){
	int n;
	ll ans=0,sum=0,maxn=0;
	cin>>n;
	for(int i=0;i<n;i++) cin>>arr[i].a>>arr[i].b;
	for(int i=0;i<n;i++){
		sum+=max(arr[i].a,arr[i].b);
		ans+=min(arr[i].a,arr[i].b)*min(arr[i].a,arr[i].b);
		maxn=max(maxn,min(arr[i].a,arr[i].b));
	}
	sum+=maxn;
	ans-=(maxn*maxn);
	ans+=sum*sum;
	cout<<ans<<'\n';
	return;
}
int main(){
	iofast
	int t;
	cin>>t;
	w(t) solve();
	return 0;
}

Note $$$mx=max(a_1,a_2,\ldots,a_n)$$$ and $$$mn=min(a_1,a_2,\ldots,a_n)$$$.

Case $$$1$$$: $$$mx-mn>1$$$, the answer is $$$0$$$.

Case $$$2$$$: $$$mx=mn$$$

• if $$$mx=n-1$$$, the answer is $$$3$$$ when $$$n=2$$$ and $$$1$$$ otherwise;

• otherwise, we can see all numbers are not unique. This problem is equivalent to: there are $$$n$$$ balls and $$$mx$$$ boxes, and the balls and boxes are the same. Find the number of solutions where each box has at least two balls. This is a variation of a classic problem, and the answer is $$$C(n-mx-1,mx-1)$$$(don't forge to check $$$n \ge 2mx$$$).

Case $$$3$$$: $$$mx=mn+1$$$

For $$$a_i=mn$$$, we can see $$$b_i$$$ are unique and for $$$a_i=mx$$$, $$$b_i$$$ are not unique. We first assign unique numbers, and then the problem is transformed into Case $$$2$$$.

The time complexity is $$$O(n)$$$.

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define fast                       \
 ios_base::sync_with_stdio(0);      \
 cin.tie(0);                         \
 cout.tie(0);
 
ll mod=998244353;
 
long long power(long long a,long long b){
  long long x=1,y=a;
  while(b>0){
    if(b&1ll){
      x=(x*y)%mod;
    }
    y=(y*y)%mod;
    b>>=1;
  }
  return x%mod;
}
 
long long modular_inverse(long long n){
  return power(n,mod-2);
}
 
#define MAXN 2000005
 
long long factorial[MAXN];
long long invfact[MAXN];
 
void cfact(){
  long long i;
  factorial[0]=1;
  factorial[1]=1;
  for(i=2;i<MAXN;i++){
    factorial[i]=factorial[i-1]*i;
    factorial[i]%=mod;
  }
  invfact[MAXN-1]=modular_inverse(factorial[MAXN-1]);
  for(i=MAXN-2;i>=0;i--){
    invfact[i]=invfact[i+1]*(i+1);
    invfact[i]%=mod;
  }
}
 
long long calcnCr(long long n,long long k){
  if(k<0 || n<k){return 0;}
  return (factorial[n]*((invfact[k]*invfact[n-k])%mod))%mod;
}
 
int main(){
    fast;
    cfact();
    ll t;
    cin>>t;
    while(t--){
        ll n;
        cin>>n;
        vector<ll> a(n);
        for(ll i=0;i<n;i++) cin>>a[i];
        ll maxi=*max_element(a.begin(),a.end());
        ll mini=*min_element(a.begin(),a.end());
        ll res=0;
        if(maxi==mini){
            if(maxi==(n-1)){
                res=1;
                if(n==2) res=3;
            }
            else if(maxi<=(n/2)){
                ll m=(a[0]);
                res=calcnCr(n,m);
                res=(res*calcnCr(n-m-1,m-1))%mod;
            }
        }
        else if(maxi==(mini+1)){
            ll cntmax=count(a.begin(),a.end(),maxi);
            ll cntmin=count(a.begin(),a.end(),mini);
            if(maxi>cntmin && maxi<=cntmin+(cntmax/2)){
                ll m=maxi,m1=mini;
                m1=count(a.begin(),a.end(),m1);
                res=calcnCr(n,m);
                res=(res*calcnCr(m,m1))%mod;
                res=(res*calcnCr(n-m-1,m-m1-1))%mod;
            }
        }
        cout<<res<<"\n";
    }
}

Consider we already get the answer for $$$[i,r](1 \le i \le r)$$$, we can use it to get the answer for $$$[i,r+1](1 \le i \le r+1)$$$.

Note $$$pre_i$$$ is the max index such that $$$pre_i<i$$$ and $$$a_{pre_i}=a_i$$$. At first, $$$answer[r+1,r+1]=0$$$. For $$$answer[i,r+1](1 \le i \le r)$$$, there are two cases:

• $$$answer[i,r+1]=answer[i,r]$$$. We won't make any changes;

• $$$answer[i,r+1]=a_{i+1}$$$. It is only possible for $$$1 \le i \le pre_i$$$. We can use a lazy tag segment tree to maintain the answer.

The time complexity will be $$$O(n\ log\ n)$$$ or $$$O(n\ log^2\ n)$$$ depends on your implementation.

// Author: sendyuripics
// Created: 2024.09.13 21:28:43
// Url: https://mirror.codeforces.com/gym/547746/problem/F

#include<bits/stdc++.h>
#define int long long
using namespace std;
void ts(){cout<<"IAKIOI\n";}
inline int read(){
	int n=0,f=1,ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		n=n*10+ch-'0';
		ch=getchar();
	}
	return n*f;
}
//max once, max twice
int N;
int a[200005];
int o[200005];
int lst[200005];
using ll = long long;
const int MAXN = 200001;
const ll llINF=(1ll<<60);  // 1-based
ll A[MAXN];

struct Node {
	ll sum;   // Sum tag
	ll max1;  // Max value
	ll max2;  // Second Max value
	ll maxc;  // Max value count
	ll min1;  // Min value
	ll min2;  // Second Min value
	ll minc;  // Min value count
	ll lazy;  // Lazy tag
} T[MAXN * 4];

void merge(int t) {
	// sum
	T[t].sum = T[t << 1].sum + T[t << 1 | 1].sum;

	// max
	if (T[t << 1].max1 == T[t << 1 | 1].max1) {
		T[t].max1 = T[t << 1].max1;
		T[t].max2 = max(T[t << 1].max2, T[t << 1 | 1].max2);
		T[t].maxc = T[t << 1].maxc + T[t << 1 | 1].maxc;
	} else {
		if (T[t << 1].max1 > T[t << 1 | 1].max1) {
			T[t].max1 = T[t << 1].max1;
			T[t].max2 = max(T[t << 1].max2, T[t << 1 | 1].max1);
			T[t].maxc = T[t << 1].maxc;
		} else {
			T[t].max1 = T[t << 1 | 1].max1;
			T[t].max2 = max(T[t << 1].max1, T[t << 1 | 1].max2);
			T[t].maxc = T[t << 1 | 1].maxc;
		}
	}

	// min
	if (T[t << 1].min1 == T[t << 1 | 1].min1) {
		T[t].min1 = T[t << 1].min1;
		T[t].min2 = min(T[t << 1].min2, T[t << 1 | 1].min2);
		T[t].minc = T[t << 1].minc + T[t << 1 | 1].minc;
	} else {
		if (T[t << 1].min1 < T[t << 1 | 1].min1) {
			T[t].min1 = T[t << 1].min1;
			T[t].min2 = min(T[t << 1].min2, T[t << 1 | 1].min1);
			T[t].minc = T[t << 1].minc;
		} else {
			T[t].min1 = T[t << 1 | 1].min1;
			T[t].min2 = min(T[t << 1].min1, T[t << 1 | 1].min2);
			T[t].minc = T[t << 1 | 1].minc;
		}
	}
}

void push_add(int t, int tl, int tr, ll v) {
	if (v == 0) { return; }
	T[t].sum += (tr - tl + 1) * v;
	T[t].max1 += v;
	if (T[t].max2 != -llINF) { T[t].max2 += v; }
	T[t].min1 += v;
	if (T[t].min2 != llINF) { T[t].min2 += v; }
	T[t].lazy += v;
}

// corresponds to a chmin update
void push_max(int t, ll v, bool l) {
	if (v >= T[t].max1) { return; }
	T[t].sum -= T[t].max1 * T[t].maxc;
	T[t].max1 = v;
	T[t].sum += T[t].max1 * T[t].maxc;
	if (l) {
		T[t].min1 = T[t].max1;
	} else {
		if (v <= T[t].min1) {
			T[t].min1 = v;
		} else if (v < T[t].min2) {
			T[t].min2 = v;
		}
	}
}

// corresponds to a chmax update
void push_min(int t, ll v, bool l) {
	if (v <= T[t].min1) { return; }
	T[t].sum -= T[t].min1 * T[t].minc;
	T[t].min1 = v;
	T[t].sum += T[t].min1 * T[t].minc;
	if (l) {
		T[t].max1 = T[t].min1;
	} else {
		if (v >= T[t].max1) {
			T[t].max1 = v;
		} else if (v > T[t].max2) {
			T[t].max2 = v;
		}
	}
}

void pushdown(int t, int tl, int tr) {
	if (tl == tr) return;
	// sum
	int tm = (tl + tr) >> 1;
	push_add(t << 1, tl, tm, T[t].lazy);
	push_add(t << 1 | 1, tm + 1, tr, T[t].lazy);
	T[t].lazy = 0;

	// max
	push_max(t << 1, T[t].max1, tl == tm);
	push_max(t << 1 | 1, T[t].max1, tm + 1 == tr);

	// min
	push_min(t << 1, T[t].min1, tl == tm);
	push_min(t << 1 | 1, T[t].min1, tm + 1 == tr);
}

void build(int t = 1, int tl = 0, int tr = N - 1) {
	T[t].lazy = 0;
	if (tl == tr) {
		T[t].sum = T[t].max1 = T[t].min1 = A[tl];
		T[t].maxc = T[t].minc = 1;
		T[t].max2 = -llINF;
		T[t].min2 = llINF;
		return;
	}

	int tm = (tl + tr) >> 1;
	build(t << 1, tl, tm);
	build(t << 1 | 1, tm + 1, tr);
	merge(t);
}

void update_add(int l, int r, ll v, int t = 1, int tl = 0, int tr = N - 1) {
	if (r < tl || tr < l) { return; }
	if (l <= tl && tr <= r) {
		push_add(t, tl, tr, v);
		return;
	}
	pushdown(t, tl, tr);

	int tm = (tl + tr) >> 1;
	update_add(l, r, v, t << 1, tl, tm);
	update_add(l, r, v, t << 1 | 1, tm + 1, tr);
	merge(t);
}

void update_chmin(int l, int r, ll v, int t = 1, int tl = 0, int tr = N - 1) {
	if (r < tl || tr < l || v >= T[t].max1) { return; }
	if (l <= tl && tr <= r && v > T[t].max2) {
		push_max(t, v, tl == tr);
		return;
	}
	pushdown(t, tl, tr);

	int tm = (tl + tr) >> 1;
	update_chmin(l, r, v, t << 1, tl, tm);
	update_chmin(l, r, v, t << 1 | 1, tm + 1, tr);
	merge(t);
}

void update_chmax(int l, int r, ll v, int t = 1, int tl = 0, int tr = N - 1) {
	if (r < tl || tr < l || v <= T[t].min1) { return; }
	if (l <= tl && tr <= r && v < T[t].min2) {
		push_min(t, v, tl == tr);
		return;
	}
	pushdown(t, tl, tr);

	int tm = (tl + tr) >> 1;
	update_chmax(l, r, v, t << 1, tl, tm);
	update_chmax(l, r, v, t << 1 | 1, tm + 1, tr);
	merge(t);
}

ll query_sum(int l, int r, int t = 1, int tl = 0, int tr = N - 1) {
	if (r < tl || tr < l) { return 0; }
	if (l <= tl && tr <= r) { return T[t].sum; }
	pushdown(t, tl, tr);

	int tm = (tl + tr) >> 1;
	return query_sum(l, r, t << 1, tl, tm) + query_sum(l, r, t << 1 | 1, tm + 1, tr);
}
void solve(){
	N=read();
	map<int,int> mp;
	for(int i=0;i<N;i++){
		a[i]=read();
		lst[i]=(mp.count(a[i])?mp[a[i]]:-1ll);
		mp[a[i]]=i;
		o[i]=0;
	}
	build();
	int res=0;
	for(int i=0;i<N;i++){
		if(lst[i]!=-1)update_chmax(0,lst[i],a[i]);
		res+=query_sum(0,N-1);
	}
	cout<<res<<"\n";
}
signed main(){
	int t=read();
	while(t--)solve();
	return 0;
}
//look at my code
//my code is amazing

Use a variant of the Euler tour. Let's call it BFS-children-first-DFS.

First, node $$$1$$$ is added to the sequence, then $$$DFS(1)$$$ is performed. When $$$DFS(x)$$$ is called, all child nodes of $$$x$$$ are added to the sequence, and then $$$DFS(son[x][i])$$$ is performed.

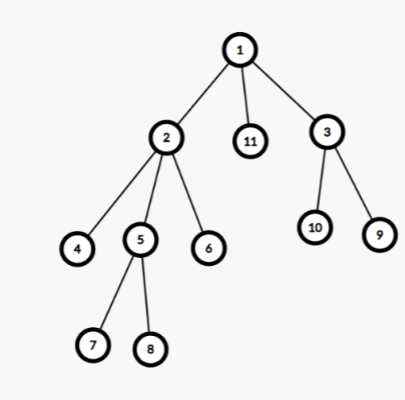
For example, for the tree shown above, the BFS-children-first-DFS order is $$$[1,2,11,3,4,5,6,7,8,10,9]$$$.

In this way, the subtree rooted at node $$$x$$$ (excluding $$$x$$$ itself) and all the child nodes of node $$$x$$$ are within a contiguous segment of the sequence. This makes it easy to maintain the operations in $$$O(n log n)$$$.

#include <bits/stdc++.h>
#define GO cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);
typedef long long ll;
using namespace std;
const int N = 3e5 + 50;
vector<int> adj[N];
ll T[N * 4], lazy[N * 4];
int ind[N], in[N], out[N], out2[N];
int Time = 1;
int n;

void push(int x, int l, int r){
    if(!lazy[x]) return;
    T[x] += lazy[x];
    if(l < r){
        lazy[x * 2] += lazy[x];
        lazy[x * 2 + 1] += lazy[x];
    }
    lazy[x] = 0;
}

void update(int i, int j, int val, int x = 1, int l = 1, int r = n){
    push(x, l, r);
    if(r < i || l > j) return;
    if(l >= i && r <= j){
        lazy[x] = val;
        push(x, l, r);
        return;
    }
    int mid = (l + r) / 2;
    update(i, j, val, x * 2, l, mid);
    update(i, j, val, x * 2 + 1, mid + 1, r);
    T[x] = max(T[x * 2], T[x * 2 + 1]);
}

ll query(int i, int j, int x = 1, int l = 1, int r = n){
    push(x, l, r);
    if(r < i || l > j) return -1e18;
    if(l >= i && r <= j) return T[x];
    int mid = (l + r) / 2;
    ll q1 = query(i, j, x * 2, l, mid);
    ll q2 = query(i, j, x * 2 + 1, mid + 1, r);
    return max(q1, q2);
}

void DFS(int u = 1, int p = 1){
    bool f = 0;
    for(int v : adj[u]){
        if(v == p) continue;
        ++Time;
        if(!f) in[u] = Time;
        out[u] = Time;
        ind[v] = Time;
        f = 1;
    }
    for(int v : adj[u]){
        if(v == p) continue;
        DFS(v, u);
    }
    out2[u] = Time;
}

int main()
{
    GO
    int q;
    cin >> n >>q;
    ind[1] = 1;
    for(int i = 0; i < n - 1; i++){
        int a, b;
        cin >> a >> b;
        adj[a].push_back(b);
        adj[b].push_back(a);
    }
    DFS();
   // cin >> q;
    while(q--){
        int t;
        cin >> t;
        //
       // cout<<"t="<<t<<'\n';
        //
        if(t == 1){ //Add v to all nodes in the subtree rooted at node x
            int u, x;
            cin >> u >> x;
            update(ind[u], ind[u], x);
            if(in[u])
            update(in[u], out2[u], x);
        }
        else if(t == 2){ //Add v to all children of node x.if it has children
            int u, x;
            cin >> u >> x;
            if(in[u])
            update(in[u], out[u], x);
        }
        else if(t == 3){ //Query the maximum value in the subtree rooted at node x.
            int u;
            cin >> u;
            ll ans = query(ind[u], ind[u]);
            if(in[u]) ans = max(ans, query(in[u], out2[u]));
            cout << ans << '\n';
        }
        else{ //Query the maximum value among all children of node x if there's children otherwise print 0
            int u;
            cin >> u;
            ll ans = -1e18;
            if(in[u]) ans = max(ans, query(in[u], out[u]));
            cout << ans << '\n';
        }
    }
    return 0;
}