Submission I would like to explain the logic used to solve problem E (which I didn't manage to complete during the contest and submitted shortly after).
For this, it will be useful to know what Catalan numbers are, as well as how to derive their formula. You can read about Catalan numbers in detail, for example, on wiki: тык, Catalan numbers can be defined in different ways, but we will define the number Cn as the number of balanced bracket sequences of length 2n. We are interested in the following relatively well-known and elegant method to find this number.
Let’s consider a coordinate grid where we need to walk from (0,0) to (n,n). We can only move to the right or up. A step to the right corresponds to an opening bracket, and a step up — to a closing one. Thus, there is a one-to-one correspondence between a valid bracket sequence of length 2n and a path from (0,0) to (n,n) that does not cross the diagonal y=x; since a point above this diagonal would mean that in the current prefix, there are more closing brackets than opening ones. How can we find the number of such paths?
The total number of paths is \binom{2n}{n}. From this number, we subtract the number of invalid paths. Invalid paths are those that cross y=x, or, equivalently, have at least one common point with the line y=x+1. Take the first (with the smallest x) common point (a, a+1) and reflect the segment of the path from (0,0) to (a, a+1) across the line y=x+1. We obtain a path from (-1,1) to (n,n). This is a one-to-one correspondence. Indeed, any path starting at (0,0) that has common points with y=x+1 can be reflected up to the first such point. At the same time, any path from (-1,1) to (n,n) must have common points with с y=x+1, since the start and end points of the path are on opposite sides of the line, which means we can also reflect the segment of the path up to the first such point. The number of such invalid paths is \binom{2n}{n+1}. (or, equivalently \binom{2n}{n-1}.) Therefore, the number of valid paths is C_n = \binom{2n}{n} - \binom{2n}{n+1}. Это и есть число Каталана. Подробнее на картинке. 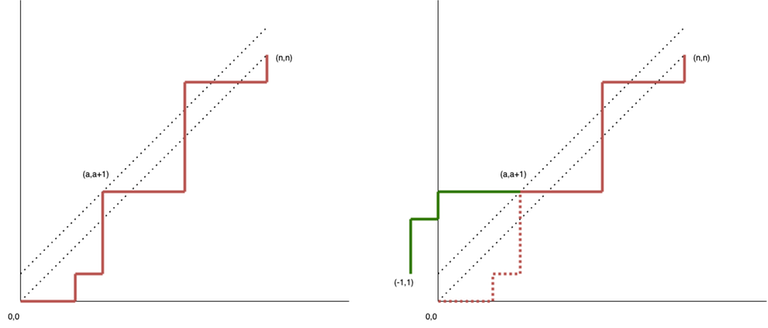
If there were no trump suit in the problem, the winning distribution of cards between the players would satisfy the condition that all cards of the same suit are distributed in the order of a balanced bracket sequence, with m/2 cards for each player. However, the presence of a trump suit requires us to make two modifications to the above formula.
First, suit 1 must still satisfy the prefix condition of a balanced bracket sequence, but it does not have to be completed. Any path from (0,0) в (a, m-a), a \ge m-a, that does not intersect y=x, satisfies the condition. The number of such paths is \binom{m}{a} - \binom{m}{a+1}. This distribution of suits will leave us with 2a - m trump cards that we can use for other suits. This is the basis of our DP. Let dp_i[ta] be the number of ways to arrange the first i suits in a winning way, leaving ta trump cards available for later use. Then dp_1[2a - m] = \binom{m}{a} - \binom{m}{a+1} \forall a \ge m/2.
Second, if we use k (even number) trump cards for suit i \ne 1, it means that player 1 plays (m - k)/2 cards of suit i and player 2 plays (m+k)/2 cards. The cards must satisfy the condition of a "not too imbalanced" bracket sequence, meaning that on any prefix, the number of closing brackets should not exceed the number of opening brackets by more than k.
Combining these ideas, we find that the result is the number of paths from (0,0) to (\frac{m - k}{2}, \frac{m + k}{2}), that do not intersect y = x + k. Invalid paths are reflected in a similar way as before, but across the line y = x + k + 1, to the paths that start at ( -(k+1), (k+1)). Thus the number of valid path is f(m,k) = \binom{m}{(m - k)/2} - \binom{m}{(m - k)/2 + k + 1}. 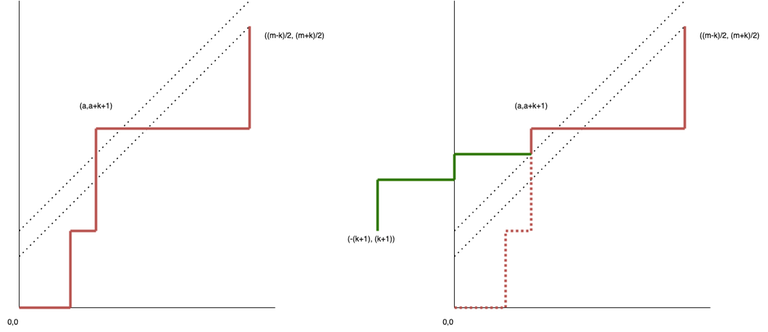
The DP transition itself is easy: \forall ta \le m, \forall k \le ta, dp_i[ta - k] += f(m,k)*dp_{i-1}[ta]. It's enough to consider only even ta и k. The final answer is dp_n[0]. The complexity is O(m^2n).






