A. Nobita and Shizuka
Author: aryan_lem
To calculate the piece with maximum area, we need the maximum length and maximum breadth. The difference between two successive horizontal cuts gives us the the breadth of smaller rectangular pieces. Similarly, the difference between two successive vertical cuts gives us length of smaller rectangular pieces. Thus, the problem boils down to calculating maximum among all successive horizontal and vertical cuts. The final answer will be the product of these two values.
The time complexity for each test case will be: O(n).
#include<bits/stdc++.h>
using namespace std;
#define int long long
int32_t main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int n,m;cin>>n>>m;
int x,y;cin>>x>>y;
int m1=0,m2=0;
int l=0,b=0;
for(int i=0;i<x;i++){int p;cin>>p;m1=max(m1,p-l);l=p;}
for(int i=0;i<y;i++){int p;cin>>p;m2=max(m2,p-b);b=p;}
m1=max(m1,n-l);
m2=max(m2,m-b);
cout<<m1*m2;
return 0;
}
B. Kang the Conquerer
Author: Utsav_Kasvala
It is easy to understand that, a monster will win only if the fight contains of other monsters with lower power. So, for every monster, we have to calculate all possible fights with weaker monsters. Here is the implementation:
First, sort the array. Then, iterate from the beginning, treating the current element as the maximum in each step. For each current element, generate all possible subsequences using the previous elements. Add the product of the current element and the number of possible subsequences to your result. The number of possible subsequences using i elements is 2^i. You can efficiently compute 2^i using binary exponentiation, or you may calculate it at every iteration.
The time complexity for each test case will be: O(n*log(n)).
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define vi vector<int>
#define all(x) (x).begin(),(x).end()
#define endl "\n"
const int mod= 1e9+7;
int32_t main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t;cin>>t;
while(t--){
int n;cin>>n;vi a(n);for(int i=0;i<n;i++)cin>>a[i];
int x=1;
int ans=0;sort(all(a));
for(int i=0;i<n;i++){
int y=x*a[i];y%=mod;
ans+=y;x*=2;x%=mod;ans%=mod;
}
cout<<ans<<endl;
}
return 0;
}
C. Balanced Card Exchange
Author: mittaludit236
Our Goal:
Udit's Cards Distribution: After the process, Udit must have an equal number of even and odd numbers. This means half of his cards should be even and half should be odd since n is always even.
Duplicates in Udit’s Cards: If Udit has any duplicate numbers on his cards, they need to be replaced with distinct numbers from the opponent. This will require exchanges.
Invalid Cases:
If Udit cannot make an even split of even and odd cards after the exchanges, then the result is impossible, and we should output -1.
If the number of cards on which Udit can perform an exchange exceeds the possible replacements available from the opponent, the task is also impossible.
Solution:
Greedy Approach: Since we need to achieve the lexicographically smallest order, the solution must greedily replace duplicates and non-balanced even/odd numbers using the smallest available cards from the opponent.
First, sort Udit's cards to handle the lexicographically smallest order after the exchanges.
Track the duplicates and imbalance. Use a map to track how many times each card appears and another map to count how many even and odd cards Udit has. Then, identify the cards that need to be exchanged (either duplicates or to balance the even/odd counts).
Find minimal exchanges. Iterate over the numbers from 1 to m (the opponent's card set) to find the smallest possible replacements for Udit’s duplicate cards or for balancing the even/odd count.
Check for infeasibility. If, after checking all replacements, Udit still can't achieve an equal number of even and odd cards or the number of distinct cards isn’t enough, output -1.
Output: If the task is possible, output the minimum number of exchanges and print the final card set in lexicographical order.
Time Complexity:
The time complexity is dominated by the sorting of Udit's cards and iterating over the possible replacements, which gives us a complexity of approximately O(n*log(n)), where n is the number of cards. Since the number of exchanges is at most n, and we process up to m potential replacements in linear time, the approach is efficient enough for the given constraints.
#include<bits/stdc++.h>
#define ll long long
#define rep(i,a,b) for(ll i=a;i<b;i++)
#define all(A) A.begin(), A.end()
#define allr(A) A.rbegin(),A.rend()
#define yes cout<<"YES"<<endl;
#define no cout<<"NO"<<endl;
const ll MOD=1000000007;
const ll MOD2=998244353;
using namespace std;
void solve(){
ll n,m;
cin >> n >> m;
vector<ll>cards(n);
map<ll,ll>vis;
map<ll,ll>count;
vector<ll>exchange;
rep(i,0,n){
cin >> cards[i];
}
sort(all(cards));
rep(i,0,n){
if(vis[cards[i]] || count[cards[i]&1]==(n/2)){
exchange.push_back(i);
}else{
count[cards[i]&1]++;
vis[cards[i]]=1;
}
}
ll pos=0;
rep(i,1,m+1){
if(pos==exchange.size()) break;
if(vis[i]==1) continue;
if(count[i&1]<n/2){
count[i&1]++;
cards[exchange[pos]]=i;
pos++;
}
}
if(pos<exchange.size()){
cout << -1 << endl;
return;
}
sort(all(cards));
cout << pos<< endl;
for(auto it:cards){
cout << it << " ";
}
cout << endl;
}
int main(){
ios_base::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
ll n=1;
while(n--){
solve();
}
}
D. How many more roads ?
Author: aryan_lem
It can be observed that, bridges are the only edges that could break the path between some pair of cities. On the other hand, if we remove any non-bridge edge, then paths still exist between different pair of nodes.
Therefore, the "states" in this problem correspond to the connected components of the new graph that will be formed when all bridges are removed from the actual edge-list.
So we need to join all pairs of vertices that belong to same component. The final answer will be all possible edges among the vertices of the connected component minus the already existing edges from the actual graph excluding the bridges.
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define vi vector<int>
#define all(x) (x).begin(), (x).end()
#define endl "\n"
const int mod = 1e9 + 7;
int n, m, timer;
vector<vector<int>> adj;
vector<int> tin, low, vis;
set<pair<int, int>> bridges;
void findBridges(int nd, int parent) {
vis[nd] = 1;
tin[nd] = low[nd] = timer++;
for (int cd : adj[nd]) {
if (cd == parent) continue;
if (!vis[cd]) {
findBridges(cd, nd);
low[nd] = min(low[nd], low[cd]);
if (low[cd] > tin[nd]) {
bridges.insert({nd, cd});
bridges.insert({cd, nd});
}
} else {
low[nd] = min(low[nd], tin[cd]);
}
}
}
int componentSize = 0;
void dfs(int nd) {
vis[nd] = 1;
componentSize++;
for (int cd : adj[nd]) {
if (!vis[cd] && bridges.find({nd, cd}) == bridges.end()) {
dfs(cd);
}
}
}
int32_t main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cin >> n >> m;
adj.resize(n + 1);
tin.resize(n + 1, -1);
low.resize(n + 1, -1);
vis.resize(n + 1, 0);
timer = 0;
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
for (int i = 1; i <= n; i++) {
if (!vis[i]) {
findBridges(i, -1);
}
}
fill(all(vis), 0);
vector<int> componentSizes;
for (int i = 1; i <= n; i++) {
if (!vis[i]) {
componentSize = 0;
dfs(i);
componentSizes.push_back(componentSize);
}
}
int ans = 0;
for (int size : componentSizes) {
ans += (size * (size - 1)) / 2;
}
cout << ans - m + (bridges.size() / 2) << endl;
return 0;
}
E. Logical Zoro!
Author: mr.awasthi_
The problem emphasizes on the knowledge of properties of logical operators and binary search. For the initially provided equation, you need to have the knowledge of 2 major relations between arithmetic and logical operators given as: (You can read about the proofs of the equations on internet)
A|B + A&B = A+B ->(i)
A^B + 2(A&B) = A+B ->(ii)
By adding both equations and rearranging the terms, we obtain the relation:
2(A+B) - 3(A&B) - (A|B) = A^B
Thus on comparing the equations we have the equality as:
A^B = K
Now, the problem reduces to finding the number of pairs (A, B) and their count whose XOR equals K which could be easily found out using the logic of prefix Sum.
On a single iteration, we can keep counting the frequency of each element and when we are standing at a number A, we can check for the count of A^K previously found. That would give us the count of pairs (A, B) satisfying the equation.
On the second array, we can keep an array for each element occurring in the array which will store the indexes of their occurrence in sorted fashion.
Once we have found out the count of each pair (A, B), we can use lower bound and upper bound to find the first index greater than equal to A and last index less than equal to B in the array of (A+B)/2 and multiply it with count of (A, B).
Time Complexity : O(n*log(n))
#include <bits/stdc++.h>
using namespace std;
#define int long long
void solve() {
int n, k;
cin >> n >> k;
vector<int> a(n), b(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
map<int, vector<int>> pref;
for (int i = 0; i < n; i++) {
cin >> b[i];
pref[b[i]].push_back(i + 1);
}
map<int, int> freq;
map<pair<int, int>, int> mp;
for (int i = 0; i < n; i++) {
int other = a[i] ^ k;
if (freq.count(other)) {
int x = other, y = a[i];
if (x > y) swap(x, y);
int num = (x + y) / 2;
vector<int>& vec = pref[num];
int left = lower_bound(vec.begin(), vec.end(), x) - vec.begin();
int right = lower_bound(vec.begin(), vec.end(), y) - vec.begin();
if (right == vec.size() || vec[right] > y) {
right--;
}
int count = max(0LL, right - left + 1);
count *= freq[other];
if (other > a[i]) {
mp[{a[i], other}] += count;
} else {
mp[{other, a[i]}] += count;
}
}
freq[a[i]]++;
}
if (mp.empty()) {
cout << -1 << endl;
return;
}
for (const auto& p : mp) {
cout << p.first.first << " " << p.first.second << " " << p.second << endl;
}
cout << endl;
}
int32_t main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
solve();
return 0;
}
F. Democracy Prevails
Author: Utsav_Kasvala, Editorial by: aryan_lem
It is easier to calculate paths with no leader and paths with exactly 1 leader, than paths with more than 1 leader. We can find the answer for each subtree.
Lets first see how we can calculate paths with exactly one leader.
Imagine we are at a node, with a leader, then the number of paths with exactly one leader with this node as one end point will be equal to number of nodes in this subtree, simple path to which will contain no other leader. Also, with this node as a middle node of a path, with end-nodes from two different child's subtree, simple path to which contains no other leader, will also give us paths with exactly one leader.
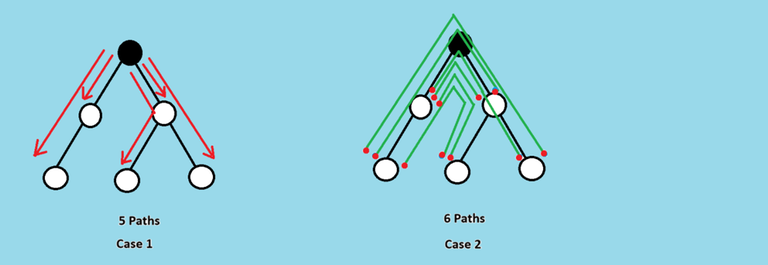
Now imagine being at a node without a leader. With this node as one end point, the number of nodes in the subtree of this node, path to which contains exactly one leader, will give us paths with exactly one leader. Also, a combination of nodes as end points from two child's subtree of this node, simple path to one containing exactly one leader node and the other containing no leader node, will also give us paths with exactly one leader, with this node as middle node for all these paths.
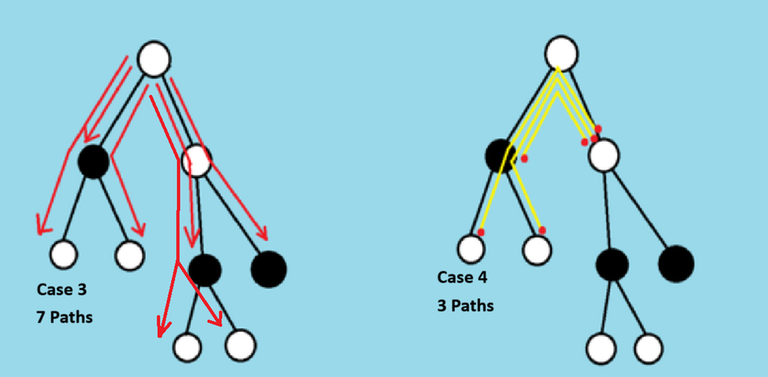
Our final answer will be equal to total possible paths minus the paths with exactly one leader.
For counting the number of paths with exactly one leader, we define 2 dp arrays,
dp1[node]=number of paths starting from this node, ending at any of its subtree node, containing no leader node.
dp2[node]=number of paths starting from this node, ending at any of its subtree node, containing exactly one leader node.
If current node contains a leader,
$$$dp1[\text{node}] = 0$$$ and
$$$dp2[\text{node}] = 1 + \sum_{i=1}^{m} dp1[\text{child}_i]$$$, where $$$child_i$$$ is the child node of the current node, m = number of direct children of this node.
The number of paths containing exactly one leader generated from nodes in this subtree = $$$dp2[\text{node}] + \sum_{i,j}^{1<=i<j<=m} dp1[\text{child}_i] * dp1[\text{child}_j]$$$.
Similarly, if current node does not contain any leader
$$$dp1[\text{node}] = 1 + \sum_{i=1}^{m} dp1[\text{child}_i]$$$
$$$dp2[\text{node}] = \sum_{i=1}^{m} dp2[\text{child}_i]$$$
The number of paths containing exactly one leader generated from nodes in this subtree = $$$dp2[\text{node}] + \sum_{i,j}^{1<=i,j<=m} dp2[\text{child}_i] * dp1[\text{child}_j]$$$.
The final answer will be all total paths minus the paths with exactly one leader.
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl "\n"
#define all(x) (x).begin(),(x).end()
int n,m;
vector<int>ldr;
vector<vector<int>>adj;
vector<int>white,black;/*white stores number of paths with all
white nodes starting from i to any node in its subtree
and black contains number of paths with 1 black node starting from i
to any node in the subtree
*/
/*here, white means no leader and black means leader*/
int ans=0;
bool leaf(int nd){if(nd!=1 && adj[nd].size()==1)return 1;if(n==1)return 1;return 0;}
void dfs(int nd,int par){
if(leaf(nd)){
if(ldr[nd]){black[nd]++;ans++;}
else white[nd]++;
return;
}
int k=0;
for(int cd:adj[nd])if(cd!=par){dfs(cd,nd);k++;}
vector<int>bsub(k),wsub(k);
int i=0;
for(int cd:adj[nd]){
if(cd!=par){
bsub[i]=black[cd];wsub[i]=white[cd];i++;
}
}
if(ldr[nd]){
int sum=(int)accumulate(all(wsub),0);
ans+=(1+sum);
int x=0;
for(int cd=0;cd<k;cd++)x+=((sum-wsub[cd])*(wsub[cd]));
x/=2;ans+=x;
white[nd]=0;
black[nd]=1+sum;
}
else{
int sum1=accumulate(all(bsub),0);
int sum2=accumulate(all(wsub),0);
ans+=sum1;
int x=0;
for(int cd=0;cd<k;cd++)x+=((sum2-wsub[cd])*(bsub[cd]));
ans+=x;
white[nd]=(1+sum2);
black[nd]=sum1;
}
}
int32_t main(){
cin>>n>>m;
ldr.resize(n+1);adj.resize(n+1);white.resize(n+1);black.resize(n+1);
for(int i=0;i<m;i++){int x;cin>>x;ldr[x]=1;}
for(int i=0;i<n-1;i++){int u,v;cin>>u>>v;adj[u].push_back(v);adj[v].push_back(u);}
dfs(1,0);
cout<<((n+1)*(n))/2-ans;
return 0;
}
G. Binary Arrays
Author: Utsav_Kasvala
First, we can use a prefix sum to track the count of zeroes and ones in a subarray. If two prefix sums are identical, it indicates that the number of zeroes and ones in the corresponding subarray is equal. To achieve this, we can modify the prefix sum by treating any element a[i] = 0 as a[i] = -1.
Next, Mo's algorithm can be applied for offline query processing. We can keep track of the frequency of each prefix sum using an unordered_map, which allows constant time access, even when the prefix sums are negative. The queries are sorted into blocks of size √n, and we continuously update the boundaries of the current segment. Before each addition, we increment the result by the number of times that prefix sum has appeared before, as it represents the number of subarrays with an equal count of zeroes and ones. Similarly, we remove previously counted subarrays from the result when deleting.
The time complexity of this approach is O((n + q)√n).
#include<bits/stdc++.h>
using namespace std;
//-----------------------------------------------------------------------------------------
#define hi_bro ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define test int T; cin>>T; for(int t=1;t<=T;t++)
#define ll long long
#define ld long double
#define yes cout<<"YES"<<endl
#define no cout<<"NO"<<endl
#define f(i,x,n) for(int i = x; i < n; i++)
#define fo(i,x,n) for(int i=x;i>=n;i--)
#define pb push_back
#define pp pop_back()
#define fi first
#define se second
#define all(v) (v).begin(), (v).end()
#define array_le_le ll a[n]; f(i,0,n){cin>>a[i];}
//-----------------------------------------------------------------------------------------
const ll mod=1e9+7;
vector<ll> prefix(1<<20,0);
unordered_map<ll,ll> freq;
vector<ll> arr(1<<20,0);
ll block,ans=0;
struct query{
ll l;
ll r;
ll ind;
};
bool cmp(query x,query y){
if(x.l/block!=y.l/block){
return (x.l/block) < (y.l/block);
}
return x.r<y.r;
}
void add(ll ind){
ans+=freq[prefix[ind]];
freq[prefix[ind]]++;
}
void remove(ll ind){
freq[prefix[ind]]--;
ans-=freq[prefix[ind]];
}
vector<ll> mo_algorithm(vector<query> q){
sort(q.begin(),q.end(),cmp);
ll l=0,r=-1;
vector<ll> temp(q.size(),0);
for(ll i=0;i<q.size();i++){
ll ql=q[i].l,qr=q[i].r;
while(l>ql){
l--;
add(l);
}
while(r<qr){
r++;
add(r);
}
while(l<ql){
remove(l);
l++;
}
while(r>qr){
remove(r);
r--;
}
temp[q[i].ind]=ans;
}
return temp;
}
void solve()
{
ll n,q;
cin>>n>>q;
block=sqrt(n);
for(int i=0;i<n;i++){
cin>>arr[i];
}
for(int i=1;i<=n;i++){
if(arr[i-1]==0)arr[i-1]=-1;
prefix[i]=prefix[i-1]+arr[i-1];
}
vector<query> op(q);
for(int i=0;i<q;i++){
ll x,y;
cin>>x>>y;
x--;
op[i].l=x;
op[i].r=y;
op[i].ind=i;
}
vector<ll> fans=mo_algorithm(op);
for(auto &val:fans)cout<<val<<"\n";
}
int main()
{
hi_bro;
solve();
return 0;
}
H. Survival Quest!
Author: mr.awasthi_
This problem emphasizes on the knowledge of Binary lifting on trees and prefix Sum.
First, we need to understand that the travellers will only meet if their height in the tree is equal, else they will either we caught in any country on their way or they will reach the Union Bank of the World. So, first we need to calculate the height of each node from the root 0.
Second, to calculate the total exit tax paid by a traveller on their, we need to sum up all the exit taxes the the point reachable, which could be calculated using prefix sum using formula.
Total tax = cost[currentNode]-cost[lastReachableNode]
So, we need to maintain a prefix Sum of taxes for each country from 0 also.
Noe, the logic is, if the given countries have their heights equal, then they will definitely meet at their lowest common ancestor. Now, to find the LCA of two nodes, you need to have the knowledge of binary lifting.
Once, the LCA is found, their can be Three cases: 1. Both of them are reachable till their, so the remaining money of both of them would be added in the countries bank. 2. Either One of them gets caught previously, so the other one can go to the Union Bank if possible. 3. Both of them caught before meeting.
If they meet, the remaining money is added to the countries bank, and if they don't meet, then if they can reach Country 0, there money will be added to Union Bank else they get caught up.
Time Complexity: O(nlogn) + O(q) = O(n*log(n))
#include<bits/stdc++.h>
using namespace std;
#define int long long
int subtree[200001];
int lca[200001][18];
void dfsFirst(int node, int parent, vector<int> &vis, vector<int> &cost, vector<vector<int>> &tree){
vis[node]=1;
if(parent!=-1) {
subtree[node]=subtree[parent]+1;
cost[node]=cost[node]+cost[parent];
}
else subtree[node]++;
lca[node][0]=parent;
for(auto child: tree[node]){
if(vis[child]) continue;
dfsFirst(child, node, vis, cost, tree);
}
}
int findLca(int u, int v){
if(subtree[v]>subtree[u]) return findLca(v, u);
int d=subtree[u]-subtree[v];
int first=u; int second=v;
while(d>0){
int power=log2(d);
first=lca[first][power];
d=d-pow(2, power);
}
for(int i=17; i>=0; i--){
if(lca[first][i]!=-1 && lca[second][i]!=-1 && lca[first][i]!=lca[second][i]){
first=lca[first][i]; second=lca[second][i];
}
}
return lca[first][0];
}
void solve() {
int n, m; cin>>n>>m;
vector<int> cost(n);
for(int i=0; i<n; i++){
cin>>cost[i];
}
vector<vector<int>> tree(n);
for(int i=0; i<m; i++){
int u, v; cin>>u>>v;
tree[u].push_back(v);
tree[v].push_back(u);
}
memset(subtree, 0, sizeof subtree);
memset(lca, -1, sizeof lca);
vector<int> vis(n, 0);
dfsFirst(0, -1, vis, cost, tree);
for(int i=1; i<18; i++){
for(int j=0; j<n; j++){
int parent=lca[j][i-1];
if(parent!=-1){
lca[j][i]=lca[parent][i-1];
}
}
}
vector<int> final(n, 0);
int q; cin>>q;
while(q--){
int u, v, x, y; cin>>u>>v>>x>>y;
if(subtree[u]==subtree[v]){
int parent=findLca(u, v);
int uCost=cost[u]-cost[parent];
int vCost=cost[v]-cost[parent];
x=x-uCost; y=y-vCost;
if(x>=0 && y>=0){
final[parent]=final[parent]+(x+y);
}
else if(x<0 && y>=0){
y=y-(cost[parent]-cost[0]);
if(y>=0){
final[0]=final[0]+y;
}
}
else if(x>=0 && y<0){
x=x-(cost[parent]-cost[0]);
if(x>=0){
final[0]=final[0]+x;
}
}
}
else{
x=x-(cost[u]-cost[0]);
y=y-(cost[v]-cost[0]);
if(x>=0) final[0]=final[0]+x;
if(y>=0) final[0]=final[0]+y;
}
}
bool ok=true;
for(int i=0; i<n; i++){
if(final[i]>0){
cout<<i<<" "<<final[i]<<endl;
ok=false;
}
}
if(ok) cout<<-1<<endl;
}
int32_t main() {
ios_base::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int t = 1;
//cin >> t;
int i = 1;
while (t--) {
i++;
solve();
}
return 0;
}





