Hello everyone. Today I would like to introduce you to a new technique — ternary search on non-unimodal functions. I came up with it during ROI 2024 and it helped me to become a prize winner.

The motivation

There are many examples in CP where we need to maximise or minimise the value of some function $$$f$$$. If the function is unimodal, there is no problem using ternary search. But if it's not, there's nothing to do. Of course, if $$$f$$$ is random, we should check all its values. Fortunately, intuition tells us that if the function is often close to unimodal, we can also use ternary search on a large part of its area of definition.

The intuition

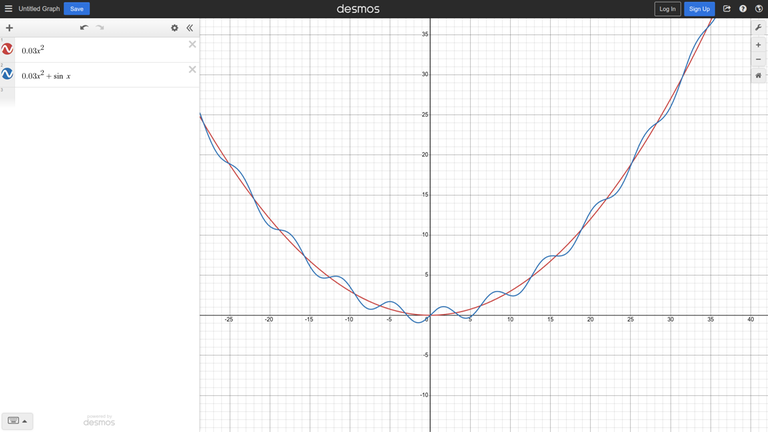
Consider the unimodal function $$$0.03x^2$$$ after adding some noise ($$$sin (x)$$$) to it:

Intuition suggests that if the noise is not strong, we can still use a ternary search away from the global minimum.

In this example, we can put it more formally — the derivative of the function is $$$0.06x + cos(x)$$$, and when $$$|x| > \frac{1}{0.06} \approx 16.67$$$, adding cosine does not change the sign of the derivative.

The first optimisation

So, the first idea is to run the ternary search using not while (r - l > eps) but while (r - l > C) and then bruteforce all values between $$$l$$$ and $$$r$$$ with some precision. In many cases when $$$f$$$ takes an integer argument there will be no precision issue at all.

The second optimisation

I should mention this blog. It tells us a similar idea of splitting all argument values into blocks and applying ternary search on them.

This is the only thing related to the blog that I found. I tried googling and asking people involved in CP, but none of them knew about it before.

Testing

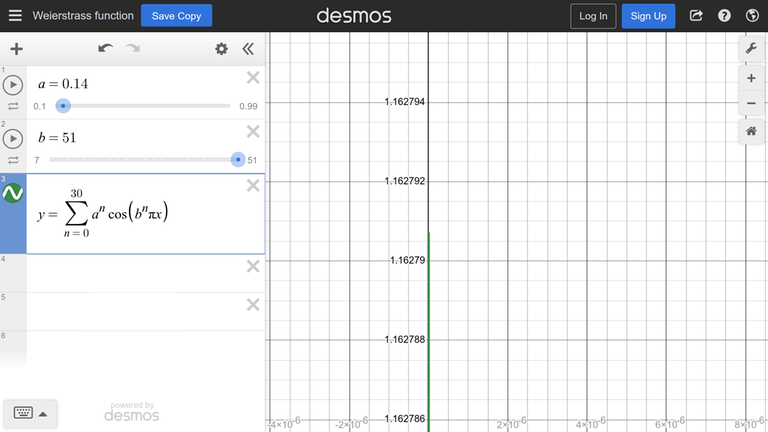
The function from the example is boring, so consider a more interesting function: Weierstrass function

We zoom in and find that the maximum is about $$$1.162791$$$

We will search for maximum on the interval (-1, 1).

#include <bits/stdc++.h>
#define M_PI 3.14159265358979323846
using namespace std;
#define ld long double
ld Weierstrass(ld x) {
    ld y = 0;
    for (int i = 0; i < 30; i++) y += pow(0.14, i) * cos(pow(51, i) * M_PI * x);
    return y;
}
ld Classical_ternary(ld f(ld), ld l = -1, ld r = 1, ld eps = 1e-7) {
    while (r - l > eps) {
        ld midl = l + (r - l) / 3;
        ld midr = r - (r - l) / 3;
        if (f(midl) > f(midr)) r = midr;
        else l = midl;
    }
    return f(l);
}
int main() {
    cout << Classical_ternary(Weierstrass) << endl;
}

This gives us $$$1.12881$$$. Changing $$$eps$$$ will slightly change this value.

Let's split arguments into blocks. Since the arguments are real, in fact we are not going to split them explicitly into blocks, we will take the minimum in some range near the argument.

ld Blocks(ld f(ld), ld l = -1, ld r = 1, ld eps = 1e-7) {
    int iter = 10000;
    while (r - l > eps) {
        ld midl = l + (r - l) / 3;
        ld midr = r - (r - l) / 3;
        ld vall = -2e9, valr = -2e9;
        for (ld x = midl, i = 0; i < iter; x += eps, i++) vall = max(vall, f(x));
        for (ld x = midr, i = 0; i < iter; x += eps, i++) valr = max(valr, f(x));
        if (vall > valr) r = midr;
        else l = midl;
    }
    return f(l);
}

It gives $$$1.15616$$$, which is quite good. We can optimise it by taking maximum among all values of $$$f$$$ we have ever computed:

It gives us $$$1.16278$$$, which is very close to expected $$$1.162791$$$. Seems like we have succeed.

But there are some troubles with choosing

The third optimisation

Let's change the constant $$$3$$$ in the code. We will call it C. It is not new to experienced people, often it is good to choose C equal to 2 (binary search by the derivative) or $$$\frac{\sqrt5+1}{2}$$$ (golden ratio). Since we are cutting out $$$\frac{1}{C}$$$ part of our interval on each iteration, as C grows, the probability of maxi