**_Доброго времени суток!_**↵
↵
Предлагаю обсудить задачи прошедшей олимпиады. По ходу буду добавлять разборы.↵
↵
_**Разбор задач.**_↵
↵
**Задача A.**↵
↵
_Разбор от [user:Alex_2oo8,2014-115-06-249]._↵
↵
Всегда существует оптимальное решение следующего вида — разобьем всю последовательность на отрезочки и сначала заберем все числа из первого отрезочка (внутри отрезочка берем числа в обратном порядке), потом из второго отрезочка и так далее. К примеру, если мы разбили последовательность на отрезки вот так: <span class="tex-span">[<i>a</i><sub class="lower-index">1</sub> <i>a</i><sub class="lower-index">2</sub> <i>a</i><sub class="lower-index">3</sub>][<i>a</i><sub class="lower-index">4</sub> <i>a</i><sub class="lower-index">5</sub>][<i>a</i><sub class="lower-index">6</sub> <i>a</i><sub class="lower-index">7</sub> <i>a</i><sub class="lower-index">8</sub> <i>a</i><sub class="lower-index">9</sub>]</span>, то забирать числа будем в порядке <span class="tex-span"><i>a</i><sub class="lower-index">3</sub>, <i>a</i><sub class="lower-index">2</sub>, <i>a</i><sub class="lower-index">1</sub>, <i>a</i><sub class="lower-index">5</sub>, <i>a</i><sub class="lower-index">4</sub>, <i>a</i><sub class="lower-index">9</sub>, <i>a</i><sub class="lower-index">8</sub>, <i>a</i><sub class="lower-index">7</sub>, <i>a</i><sub class="lower-index">6</sub></span>. Доказывать это сейчас не буду.↵
↵
Дальше получается довольно простое ДП: <span class="tex-span"><i>f</i>(<i>k</i>) - </span> - максимальная сумма, которую можно получить убрав префикс длины <span class="tex-span"><i>k</i></span>. Переход будет такой:↵
↵
- <span class="tex-span"><i>f</i>(<i>k</i>) = <i>f</i>(<i>k</i> - 1) + <i>a</i><sub class="lower-index"><i>k</i> + 1</sub></span>, если последний отрезочек будет длины <span class="tex-span">1</span>;↵
↵
- 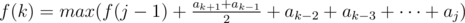, если последний отрезочек — <span class="tex-span">[<i>j</i>, <i>k</i>]</span>.↵
↵
- Замечаем, что второй переход можно записать вот так:↵
↵
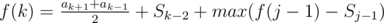, где <span class="tex-span"><i>S</i></span> — префиксные суммы и получаем константный переход.↵
↵
**Задача C.**↵
↵
_Решение от [user:Second_Hand,2014-11EXM_KG,2015-06-249]._↵
↵
После долгих размышлений я увидел закономерность. Итог:↵
↵
~~~~~↵
int s[][5] = {↵
{1, 2, 3, 4, 5},↵
{4, 5, 1, 2, 3},↵
{2, 3, 4, 5, 1},↵
{5, 1, 2, 3, 4},↵
{3, 4, 5, 1, 2},↵
};↵
int main() {↵
freopen(NAME".in", "r", stdin);↵
freopen(NAME".out", "w", stdout);↵
↵
int n, i, j, m, a[111][111];↵
↵
scanf("%d%d", &n, &m);↵
for(i = 0; i < n; i ++)↵
for(j = 0; j < m; j ++)↵
a[i][j] = s[i % 5][j % 5];↵
↵
for(i = 0; i < n; i ++){↵
for(j = 0; j < m; j ++)↵
printf("%d ", a[i][j]);↵
printf("\n");↵
}↵
↵
return 0;↵
}↵
~~~~~↵
↵
**Задача D.**↵
↵
_Разбор от [user:king_of_hakers,2014-11heavenly_phoenix,2015-06-249]._↵
↵
[Код](http://ideone.com/GaCAIx).↵
↵
**Задача E.**↵
↵
_Разбор от [user:SEFI,2014-115-06-249]._↵
↵
Простая динамика, не требует объяснения.↵
↵
↵
~~~~~↵
int main(){↵
cnt [0] = 1;↵
for (i = 1; n >= i ; i++){↵
cnt[i] += cnt[i - 1];cnt[i]%=md;↵
for (j = i - 1; j>=1 ; j--){if(a[j] > a[j + 1])break;cnt[i] += cnt[j - 1];cnt[i]%=md;}↵
for (j = i - 1; j>=1 ; j--){if(a[j] < a[j + 1])break;cnt[i] += cnt[j - 1];cnt[i]%=md;}↵
long long inter = 0;↵
for (j = i - 1; j>=1 ; j--){↵
if(a[j] != a[j + 1])break;↵
inter += cnt[j - 1];↵
}↵
cnt [i] -= inter;↵
cnt [i] = (cnt[i] + md) % md;↵
}↵
cout << cnt[ n ] << endl;↵
↵
return 0;↵
}↵
~~~~~↵
↵
**Задача G.**↵
↵
_Разбор от [user:Second_Hand,2014-11EXM_KG,2015-06-249]._↵
↵
Простой жадный алгоритм. На каждом этапе будем уравнивать предыдущий уровень с текущим пока это возможно. Если в конце остались лишние кубики (обозначим их как <span class="tex-span"><i>OST</i></span>), то ответом будет <span class="tex-span"><i>текущая высота стены + OST / N</i></span>.↵
↵
Для лучшего понимания выкладываю [код](http://ideone.com/nq7WOm).↵
↵
**Задача I.**↵
↵
_Разбор от [user:king_of_hakers,2014-11heavenly_phoenix,2015-06-249]._↵
↵
[Код](http://ideone.com/9lsMJ5).↵
↵
**Задача L.**↵
↵
_Разбор от [user:pva701,2014-115-06-249]._↵
↵
- Первый факт — рассмотрим два возможных отрезка (произвольных длин), кандидатов на ответ, для которых выполнено условие, они либо не пересекаются, либо один вкладывается в другой, потому что если они как-то пересекаются, то у этих отрезков концевые элементы равны — поэтому можем просто взять один отрезок большей длины, таким образом увеличив длину.↵
↵
- Т.е можем разбить весь массив на непересекающиеся подряд идущие отрезки. если запрос был просто на массиве — нам нужно было выбрать максимальный из этих отрезков.↵
↵
- Посчитаем для каждого <span class="tex-span"><i>i</i></span>, такой максимальный индекс <span class="tex-span"><i>f[i] (f[i] >= i)</i></span>, что отрезок <span class="tex-span"><i>[i..f[i]]</i></span> удовлетворяет условию.↵
↵
- Теперь, когда приходит запрос, начнем в <span class="tex-span"><i>l</i></span>, перейдем в <span class="tex-span"><i>f[l] + 1</i></span>, затем в <span class="tex-span"><i>f[f[l] + 1] + 1</i></span>, и т.д, т.е будем прыгать на элемент после правой границы отрезка <span class="tex-span"><i>[i..f[i]]</i></span>, сохраняя максимум среди длин всех отрезков, по которым прошли. рано или поздно наступит следующее: либо мы просто придем в <span class="tex-span"><i>r</i></span> (вернее, на следующий после <span class="tex-span"><i>r</i></span>) — тогда все, максимум найден, либо следующий прыжок из <span class="tex-span"><i>i</i></span> будет за правую границу, т.е <span class="tex-span"><i>f[i] > r</i></span>, отметим, что в этом случае <span class="tex-span"><i>a[i]</i></span> будет больше либо равен всех элементов на суффиксе <span class="tex-span"><i>[i..r]</i></span>. тогда начнем ту же самую процедуру с <span class="tex-span"><i>r</i></span> (мы так же заранее для всех <span class="tex-span"><i>j</i></span> посчитали массив <span class="tex-span"><i>g[j]</i></span> — минимальный индекс, такой что <span class="tex-span"><i>[g[j]..j]</i></span> удовлетворяет условию). рано или поздно, <span class="tex-span"><i>g[j]</i></span> станет меньше, чем <span class="tex-span"><i>l</i></span>. тогда <span class="tex-span"><i>a[j] = a[i]</i></span>, т.к. если бы они были неравны, то мы могли перейти из <span class="tex-span"><i>j</i></span> не за <span class="tex-span"><i>l</i></span> (<span class="tex-span"><i>g[j]</i></span> был бы больше <span class="tex-span"><i>l</i></span>), т.к. <span class="tex-span"><i>a[i]</i></span> был бы больше <span class="tex-span"><i>a[j]</i></span> (как мы ранее отметили). Т.е. остается один отрезок, который нельзя никак уже разбить <span class="tex-span"><i>[i..j]</i></span>, учитываем его в нашем ответе.↵
↵
- Последний шаг — все вот эти переходы (<span class="tex-span"><i>f[i]</i></span>, <span class="tex-span"><i>g[j]</i></span>) предподсчитаем в массив двоичных подъемов, и будем делать наши прыжки за <span class="tex-span"><i>log N</i></span>.↵
↵
Асимптотика — 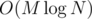↵
↵
**Задача J.**↵
↵
_Разбор от [user:netman,2014-115-06-249]._↵
↵
Сначала очень просто можно узнать, какое максимальное число вхождений у нас может быть.↵
Просто возьмем и посчитаем, какое максимальное кол-во вхождений какой-нибудь буквы мы имеем. Назовем это кол-во вхождений <span class="tex-span"><i>need</i></span>.↵
↵
Давайте научимся проверять какую-нибудь длину <span class="tex-span"><i>len</i></span>. Проверять длину <span class="tex-span"><i>len</i></span> — значит узнать, есть ли у нас такая подстрока длины <span class="tex-span"><i>len</i></span>, что она имеет <span class="tex-span"><i>need</i></span> непересекающихся вхождений.↵
↵
Это можно делать за используя полиноминальные хэши. Посчитаем хэш всех подстрок длины <span class="tex-span"><i>len</i></span>. Выпишем такие пары <span class="tex-span">(<i>hash</i>, <i>position</i>)</span> — хэш подстроки и позиция подстроки. Теперь давайте для каждого уникального <span class="tex-span"><i>hash</i></span> выпишем все его <span class="tex-span"><i>position</i></span> в возрастающем порядке. Теперь, зная все <span class="tex-span"><i>position</i></span> для фиксированного <span class="tex-span"><i>hash</i></span> не составляет труда посчитать максимальную подпоследовательность из этих позиций, что разница между соседними элементами подпоследовательности больше либо равна <span class="tex-span"><i>len</i></span> (это условие нужно, потому что мы ищем непересекающиеся вхождения). Это можно легко подсчитать используя ДП:↵
↵
Пусть <span class="tex-span"><i>a</i></span> — это подпоследовательность, в которой нужно найти максимальную подпоследовательность, чтобы соседние элементы различались не меньше чем на <span class="tex-span"><i>len</i></span>. Напоминаю, что все числа в этой последовательности в возрастающем порядке.↵
↵
Теперь можно просто считать следующее ДП:↵
↵
<span class="tex-span"><i>f</i><sub class="lower-index"><i>i</i></sub></span> — максимальная длина подпоследовательности из префикса <span class="tex-span"><i>a</i></span> длины <span class="tex-span"><i>i</i></span>. Понятно, что <span class="tex-span"><i>f</i><sub class="lower-index">0</sub> = 0</span>.↵
↵
Подсчет данного ДП ведется так:↵
↵
<span class="tex-span"><i>f</i><sub class="lower-index"><i>i</i></sub> = <i>max</i>(<i>f</i><sub class="lower-index"><i>j</i></sub>, <i>f</i><sub class="lower-index">0</sub>) + 1</span>, где <span class="tex-span"><i>j</i></span> — такая максимальная позиция, что <span class="tex-span"><i>a</i><sub class="lower-index"><i>i</i></sub> - <i>a</i><sub class="lower-index"><i>j</i></sub> ≥ <i>len</i></span>. Если такой позиции нет, то <span class="tex-span"><i>j = 0</i></span>. Найти такое <span class="tex-span"><i>j</i></span> можно бинарным поиском.↵
↵
Как говорилось выше: давайте для каждого уникального <span class="tex-span"><i>hash</i></span> выпишем все его позиции и запустим на них вышеописанное ДП. И возьмем максимум среди всех результатов запуска ДП. Это и будет максимальное кол-во непересекающихся вхождений строки, имеющей длину <span class="tex-span"><i>len</i></span>. Теперь легко проверить подходит длина <span class="tex-span"><i>len</i></span> или нет.↵
↵
Также надо заметить, что если подходит длина <span class="tex-span"><i>len</i></span>, то и длина <span class="tex-span"><i>len — 1</i></span> тоже подходит, значит можно использовать бинарный поиск, чтобы найти максимальное <span class="tex-span"><i>len</i></span>, которое подходит.↵
↵
Итоговая асимптотика решения: 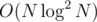↵
↵
Для лучшего понимания выкладываю [код](http://pastie.org/private/94dad4cpjxcthwaulrqpg).↵
↵
_Решение от [user:izban,2014-115-06-249]._↵
↵
Есть решение проще.↵
↵
Сначала найдем <span class="tex-span"><i>need</i></span>. Теперь фиксируем первую букву ответа (26 вариантов), и перебираем длину ответа, добавляя новый символ — суммарно будет сделано не больше <span class="tex-span"><i>n</i></span> операций для каждой буквы. Итого, решение за <span class="tex-span"><i>26n</i></span>. [Код](http://pastebin.com/2QU1hgLa).↵
↵
**P.S.** Осталось немного, отписывайтесь.
↵
Предлагаю обсудить задачи прошедшей олимпиады. По ходу буду добавлять разборы.↵
↵
_**Разбор задач.**_↵
↵
**Задача A.**↵
↵
_Разбор от [user:Alex_2oo8,201
↵
Всегда существует оптимальное решение следующего вида — разобьем всю последовательность на отрезочки и сначала заберем все числа из первого отрезочка (внутри отрезочка берем числа в обратном порядке), потом из второго отрезочка и так далее. К примеру, если мы разбили последовательность на отрезки вот так: <span class="tex-span">[<i>a</i><sub class="lower-index">1</sub> <i>a</i><sub class="lower-index">2</sub> <i>a</i><sub class="lower-index">3</sub>][<i>a</i><sub class="lower-index">4</sub> <i>a</i><sub class="lower-index">5</sub>][<i>a</i><sub class="lower-index">6</sub> <i>a</i><sub class="lower-index">7</sub> <i>a</i><sub class="lower-index">8</sub> <i>a</i><sub class="lower-index">9</sub>]</span>, то забирать числа будем в порядке <span class="tex-span"><i>a</i><sub class="lower-index">3</sub>, <i>a</i><sub class="lower-index">2</sub>, <i>a</i><sub class="lower-index">1</sub>, <i>a</i><sub class="lower-index">5</sub>, <i>a</i><sub class="lower-index">4</sub>, <i>a</i><sub class="lower-index">9</sub>, <i>a</i><sub class="lower-index">8</sub>, <i>a</i><sub class="lower-index">7</sub>, <i>a</i><sub class="lower-index">6</sub></span>. Доказывать это сейчас не буду.↵
↵
Дальше получается довольно простое ДП: <span class="tex-span"><i>f</i>(<i>k</i>) - </span> - максимальная сумма, которую можно получить убрав префикс длины <span class="tex-span"><i>k</i></span>. Переход будет такой:↵
↵
- <span class="tex-span"><i>f</i>(<i>k</i>) = <i>f</i>(<i>k</i> - 1) + <i>a</i><sub class="lower-index"><i>k</i> + 1</sub></span>, если последний отрезочек будет длины <span class="tex-span">1</span>;↵
↵
- 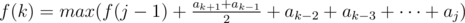, если последний отрезочек — <span class="tex-span">[<i>j</i>, <i>k</i>]</span>.↵
↵
- Замечаем, что второй переход можно записать вот так:↵
↵
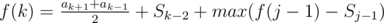, где <span class="tex-span"><i>S</i></span> — префиксные суммы и получаем константный переход.↵
↵
**Задача C.**↵
↵
_Решение от [user:
↵
После долгих размышлений я увидел закономерность. Итог:↵
↵
~~~~~↵
int s[][5] = {↵
{1, 2, 3, 4, 5},↵
{4, 5, 1, 2, 3},↵
{2, 3, 4, 5, 1},↵
{5, 1, 2, 3, 4},↵
{3, 4, 5, 1, 2},↵
};↵
int main() {↵
freopen(NAME".in", "r", stdin);↵
freopen(NAME".out", "w", stdout);↵
↵
int n, i, j, m, a[111][111];↵
↵
scanf("%d%d", &n, &m);↵
for(i = 0; i < n; i ++)↵
for(j = 0; j < m; j ++)↵
a[i][j] = s[i % 5][j % 5];↵
↵
for(i = 0; i < n; i ++){↵
for(j = 0; j < m; j ++)↵
printf("%d ", a[i][j]);↵
printf("\n");↵
}↵
↵
return 0;↵
}↵
~~~~~↵
↵
**Задача D.**↵
↵
_Разбор от [user:
↵
[Код](http://ideone.com/GaCAIx).↵
↵
**Задача E.**↵
↵
_Разбор от [user:SEFI,201
↵
Простая динамика, не требует объяснения.↵
↵
int main(){↵
cnt [0] = 1;↵
for (i = 1; n >= i ; i++){↵
cnt[i] += cnt[i - 1];cnt[i]%=md;↵
for (j = i - 1; j>=1 ; j--){if(a[j] > a[j + 1])break;cnt[i] += cnt[j - 1];cnt[i]%=md;}↵
for (j = i - 1; j>=1 ; j--){if(a[j] < a[j + 1])break;cnt[i] += cnt[j - 1];cnt[i]%=md;}↵
long long inter = 0;↵
for (j = i - 1; j>=1 ; j--){↵
if(a[j] != a[j + 1])break;↵
inter += cnt[j - 1];↵
}↵
cnt [i] -= inter;↵
cnt [i] = (cnt[i] + md) % md;↵
}↵
cout << cnt[ n ] << endl;↵
↵
return 0;↵
}↵
~~~~~↵
↵
**Задача G.**↵
↵
_Разбор от [user:
↵
Простой жадный алгоритм. На каждом этапе будем уравнивать предыдущий уровень с текущим пока это возможно. Если в конце остались лишние кубики (обозначим их как <span class="tex-span"><i>OST</i></span>), то ответом будет <span class="tex-span"><i>текущая высота стены + OST / N</i></span>.↵
↵
Для лучшего понимания выкладываю [код](http://ideone.com/nq7WOm).↵
↵
**Задача I.**↵
↵
_Разбор от [user:
↵
[Код](http://ideone.com/9lsMJ5).↵
↵
**Задача L.**↵
↵
_Разбор от [user:pva701,201
↵
- Первый факт — рассмотрим два возможных отрезка (произвольных длин), кандидатов на ответ, для которых выполнено условие, они либо не пересекаются, либо один вкладывается в другой, потому что если они как-то пересекаются, то у этих отрезков концевые элементы равны — поэтому можем просто взять один отрезок большей длины, таким образом увеличив длину.↵
↵
- Т.е можем разбить весь массив на непересекающиеся подряд идущие отрезки. если запрос был просто на массиве — нам нужно было выбрать максимальный из этих отрезков.↵
↵
- Посчитаем для каждого <span class="tex-span"><i>i</i></span>, такой максимальный индекс <span class="tex-span"><i>f[i] (f[i] >= i)</i></span>, что отрезок <span class="tex-span"><i>[i..f[i]]</i></span> удовлетворяет условию.↵
↵
- Теперь, когда приходит запрос, начнем в <span class="tex-span"><i>l</i></span>, перейдем в <span class="tex-span"><i>f[l] + 1</i></span>, затем в <span class="tex-span"><i>f[f[l] + 1] + 1</i></span>, и т.д, т.е будем прыгать на элемент после правой границы отрезка <span class="tex-span"><i>[i..f[i]]</i></span>, сохраняя максимум среди длин всех отрезков, по которым прошли. рано или поздно наступит следующее: либо мы просто придем в <span class="tex-span"><i>r</i></span> (вернее, на следующий после <span class="tex-span"><i>r</i></span>) — тогда все, максимум найден, либо следующий прыжок из <span class="tex-span"><i>i</i></span> будет за правую границу, т.е <span class="tex-span"><i>f[i] > r</i></span>, отметим, что в этом случае <span class="tex-span"><i>a[i]</i></span> будет больше либо равен всех элементов на суффиксе <span class="tex-span"><i>[i..r]</i></span>. тогда начнем ту же самую процедуру с <span class="tex-span"><i>r</i></span> (мы так же заранее для всех <span class="tex-span"><i>j</i></span> посчитали массив <span class="tex-span"><i>g[j]</i></span> — минимальный индекс, такой что <span class="tex-span"><i>[g[j]..j]</i></span> удовлетворяет условию). рано или поздно, <span class="tex-span"><i>g[j]</i></span> станет меньше, чем <span class="tex-span"><i>l</i></span>. тогда <span class="tex-span"><i>a[j] = a[i]</i></span>, т.к. если бы они были неравны, то мы могли перейти из <span class="tex-span"><i>j</i></span> не за <span class="tex-span"><i>l</i></span> (<span class="tex-span"><i>g[j]</i></span> был бы больше <span class="tex-span"><i>l</i></span>), т.к. <span class="tex-span"><i>a[i]</i></span> был бы больше <span class="tex-span"><i>a[j]</i></span> (как мы ранее отметили). Т.е. остается один отрезок, который нельзя никак уже разбить <span class="tex-span"><i>[i..j]</i></span>, учитываем его в нашем ответе.↵
↵
- Последний шаг — все вот эти переходы (<span class="tex-span"><i>f[i]</i></span>, <span class="tex-span"><i>g[j]</i></span>) предподсчитаем в массив двоичных подъемов, и будем делать наши прыжки за <span class="tex-span"><i>log N</i></span>.↵
↵
Асимптотика — 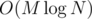↵
↵
**Задача J.**↵
↵
_Разбор от [user:netman,201
↵
Сначала очень просто можно узнать, какое максимальное число вхождений у нас может быть.↵
Просто возьмем и посчитаем, какое максимальное кол-во вхождений какой-нибудь буквы мы имеем. Назовем это кол-во вхождений <span class="tex-span"><i>need</i></span>.↵
↵
Давайте научимся проверять какую-нибудь длину <span class="tex-span"><i>len</i></span>. Проверять длину <span class="tex-span"><i>len</i></span> — значит узнать, есть ли у нас такая подстрока длины <span class="tex-span"><i>len</i></span>, что она имеет <span class="tex-span"><i>need</i></span> непересекающихся вхождений.↵
↵
Это можно делать за используя полиноминальные хэши. Посчитаем хэш всех подстрок длины <span class="tex-span"><i>len</i></span>. Выпишем такие пары <span class="tex-span">(<i>hash</i>, <i>position</i>)</span> — хэш подстроки и позиция подстроки. Теперь давайте для каждого уникального <span class="tex-span"><i>hash</i></span> выпишем все его <span class="tex-span"><i>position</i></span> в возрастающем порядке. Теперь, зная все <span class="tex-span"><i>position</i></span> для фиксированного <span class="tex-span"><i>hash</i></span> не составляет труда посчитать максимальную подпоследовательность из этих позиций, что разница между соседними элементами подпоследовательности больше либо равна <span class="tex-span"><i>len</i></span> (это условие нужно, потому что мы ищем непересекающиеся вхождения). Это можно легко подсчитать используя ДП:↵
↵
Пусть <span class="tex-span"><i>a</i></span> — это подпоследовательность, в которой нужно найти максимальную подпоследовательность, чтобы соседние элементы различались не меньше чем на <span class="tex-span"><i>len</i></span>. Напоминаю, что все числа в этой последовательности в возрастающем порядке.↵
↵
Теперь можно просто считать следующее ДП:↵
↵
<span class="tex-span"><i>f</i><sub class="lower-index"><i>i</i></sub></span> — максимальная длина подпоследовательности из префикса <span class="tex-span"><i>a</i></span> длины <span class="tex-span"><i>i</i></span>. Понятно, что <span class="tex-span"><i>f</i><sub class="lower-index">0</sub> = 0</span>.↵
↵
Подсчет данного ДП ведется так:↵
↵
<span class="tex-span"><i>f</i><sub class="lower-index"><i>i</i></sub> = <i>max</i>(<i>f</i><sub class="lower-index"><i>j</i></sub>, <i>f</i><sub class="lower-index">0</sub>) + 1</span>, где <span class="tex-span"><i>j</i></span> — такая максимальная позиция, что <span class="tex-span"><i>a</i><sub class="lower-index"><i>i</i></sub> - <i>a</i><sub class="lower-index"><i>j</i></sub> ≥ <i>len</i></span>. Если такой позиции нет, то <span class="tex-span"><i>j = 0</i></span>. Найти такое <span class="tex-span"><i>j</i></span> можно бинарным поиском.↵
↵
Как говорилось выше: давайте для каждого уникального <span class="tex-span"><i>hash</i></span> выпишем все его позиции и запустим на них вышеописанное ДП. И возьмем максимум среди всех результатов запуска ДП. Это и будет максимальное кол-во непересекающихся вхождений строки, имеющей длину <span class="tex-span"><i>len</i></span>. Теперь легко проверить подходит длина <span class="tex-span"><i>len</i></span> или нет.↵
↵
Также надо заметить, что если подходит длина <span class="tex-span"><i>len</i></span>, то и длина <span class="tex-span"><i>len — 1</i></span> тоже подходит, значит можно использовать бинарный поиск, чтобы найти максимальное <span class="tex-span"><i>len</i></span>, которое подходит.↵
↵
Итоговая асимптотика решения: 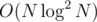↵
↵
Для лучшего понимания выкладываю [код](http://pastie.org/private/94dad4cpjxcthwaulrqpg).↵
↵
_Решение от [user:izban,201
↵
Есть решение проще.↵
↵
Сначала найдем <span class="tex-span"><i>need</i></span>. Теперь фиксируем первую букву ответа (26 вариантов), и перебираем длину ответа, добавляя новый символ — суммарно будет сделано не больше <span class="tex-span"><i>n</i></span> операций для каждой буквы. Итого, решение за <span class="tex-span"><i>26n</i></span>. [Код](http://pastebin.com/2QU1hgLa).↵
↵
**P.S.** Осталось немного, отписывайтесь.





