Hints:

div2A: Try conversions between bases.

div2B: Solve a simpler version of the problem where A_i + 1 ≠ A_i for all i.

div1A: What are the shortest paths of the vehicles? what's the shorter of those paths?

div1B: Forget about the ceiling function. Draw points (i, A[i]) and lines between them — what's the Lipschitz constant geometrically?

div1C: Some dynamic programming. Definitely not for the exp. score of one person — look at fixed scores instead.

div1D: Compute dif(v) in O(N) (without hashing) and then solve the problem in O(N²). Read my editorial of TREEPATH from Codechef.

div1E: Can you solve the problem without events of type 1 or 2? Also, how about solving it offline — as queries on subsets.

What, you thought I'd post solutions? Nope. Read the hints, maybe they'll help you. The solutions will appear here gradually.

Div. 2 A: Two Bases

It's easy to compare two numbers if the same base belong to both. And our numbers can be converted to a common base — just use the formulas

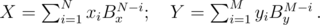
A straightforward implementation takes O(N + M) time and memory. Watch out, you need 64-bit integers! And don't use pow — iterating 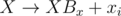is better.

Div. 2 C / Div. 1 A: The Two Routes

The condition that the train and bus can't meet at one vertex except the final one is just trolling. If there's a railway , then the train can take it and wait in town N. If there's no such railway, then there's a road , the bus can take it and wait in N instead. There's nothing forbidding this :D.

The route of one vehicle is clear. How about the other one? Well, it can move as it wants, so the answer is the length of its shortest path from 1 to N... or  - 1 if no such path exists. It can be found by BFS in time O(N + M) = O(N²).

In order to avoid casework, we can just compute the answer as the maximum of the train's and the bus's shortest distance from 1 to N. That way, we compute 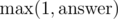; since the answer is  ≥ 1, it works well.

In summary, time and memory complexity: O(N²).

Bonus: Assume that there are M₁ roads and M₂ railways given on the input, all of them pairwise distinct.

Bonus 2: Additionally, assume that the edges are weighted. The speed of both vehicles is still the same — traversing an edge of length l takes l hours.

Div. 2 D / Div. 1 B: Lipshitz Sequence

Let 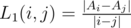for i ≠ j.

Key observation: it's sufficient to consider j = i + 1 when calculating the Lipschitz constant. It can be seen if you draw points (i, A_i) and lines between them on paper — the steepest lines must be between adjacent pairs of points.

In order to prove it properly, we'll consider three numbers A_i, A_j, A_k (i < j < k) and show that one of the numbers L₁(i, j), L₁(j, k) is  ≥ L₁(i, k). W.l.o.g., we may assume A_i ≤ A_k. There are 3 cases depending on the position of A_j relative to A_i, A_k:

• A_j > A_i, A_k — we can see that L₁(i, j) > L₁(i, k), since |A_j - A_i| = A_j - A_i > A_k - A_i = |A_k - A_i| and j - i < k - i; we just need to divide those inequalities

• A_j < A_i, A_k — this is similar to the previous case, we can prove that L₁(i, j) > L₁(j, k) in the same way

• A_i ≤ A_j ≤ A_k — this case requires more work:

  • we'll denote d_1y = A_j - A_i, d_2y = A_k - A_j, d_1x = j - i, d_2x = k - j
  • then, L₁(i, j) = d_1y / d_1x, L₁(j, k) = d_2y / d_2x, L₁(i, k) = (d_1y + d_2y) / (d_1x + d_2x)
  • let's prove it by contradiction: assume that L₁(i, j), L₁(j, k) < L₁(i, k)
  • d_1y + d_2y = L₁(i, j)d_1x + L₁(j, k)d_2x < L₁(i, k)d_1x + L₁(i, k)d_2x = L₁(i, k)(d_1x + d_2x) = d_1y + d_2y, which is a contradiction

We've just proved that to any L₁ computed for two elements A[i], A[k] with k > i + 1, we can replace one of i, j by a point j between them without decreasing L₁; a sufficient amount of such operations will give us k = i + 1. Therefore, the max. L₁ can be found by only considering differences between adjacent points.

This is actually a huge simplification — the Lipschitz constant of an array is the maximum abs. difference of adjacent elements! If we replace the array A[1..n] by an array D[1..n - 1] of differences, D[i] = A[i + 1] - A[i], then the Lipschitz constant of a subarray A[l, r] is the max. element in the subarray D[l..r - 1]. Finding subarray maxima actually sounds quite standard, doesn't it?

No segment trees, of course — there are still too many subarrays to consider.

So, what do we do next? There are queries to answer, but not too many of them, so we can process each of them in O(N) time. One approach that works is assigning a max. difference D[i] to each subarray — since there can be multiple max. D[i], let's take the leftmost one.

We can invert it to determine the subarrays for which a given D[i] is maximum: if D[a_i] is the closest difference to the left of D[i] that's  ≥ D[i] or a_i = 0 if there's none, and D[b_i] is the closest difference to the right that's  > D[i] or b_i = n - 1 if there's none (note the strict/non-strict inequality signs — we don't care about differences equal to D[i] to its right, but there can't be any to its left, or it wouldn't be the leftmost max.), then those are all subarrays D[j..k] such that a_i < j ≤ i ≤ k < b_i.

If we don't have the whole array D[1..n - 1], but only some subarray D[l..r], then we can simply replace a_i by 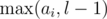and b_i by 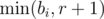. The number of those subarrays is P_i = (i - a_i)(b_i - i), since we can choose j and k independently.

All we have to do to answer a query is check all differences, take a_i, b_i (as the max/min with some precomputed values) and compute P_i; the answer to the query is 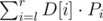. We only need to precompute all a_i, b_i for the whole array D[1..n - 1] now; that's a standard problem, solvable using stacks in O(N) time or using maps in time.

The total time complexity is O(NQ), memory O(N).

Bonus: Q ≤ 10⁵.

Div. 1 D: Acyclic Organic Compounds

The name is really almost unrelated — it's just what a tree with arbitrary letters typically is in chemistry.

If you solved problem TREEPATH from the recent Codechef November Challenge, this problem should be easier for you — it uses the same technique, after all.

Let's figure out how to compute 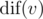for just one fixed v. One more or less obvious way is computing hashes of our strings in a DFS and then counting the number of distinct hashes (which is why there are anti-hash tests :D). However, there's another, deterministic and faster way.

Compressing the subtree T_v into a trie.

Recall that a trie is a rooted tree with a letter in each vertex (or possibly nothing in the root), where each vertex encodes a unique string read along the path from the root to it; it has at most σ sons, where σ = 26 is the size of the alphabet, and each son contains a different letter. Adding a son is done trivially in O(σ) (each vertex contains an array of 26 links to — possibly non-existent — sons) and moving down to a son with the character c is then possible in O(1).

Compressing a subtree can be done in a DFS. Let's build a trie H_v (because T_v is already used), initially consisting only of one vertex — the root containing the letter s_v. In the DFS, we'll remember the current vertex R of the tree T and the current vertex cur of the trie. We'll start the DFS at v with cur being the root of H_v; all we need to do is look at each son S of R in DFS, create the son cur_s of cur corresponding to the character s_S (if it didn't exist yet) and run DFS(S, cur_s). This DFS does nothing but construct H_v that encodes all strings read down from v in T_v. And since each vertex of H_v encodes a distinct string, 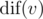is the number of vertices of H_v.

This runs in O(|T_v|σ) time, since it can create a trie with |T_v| vertices in the worst case. Overall, it'd be O(N²σ) if T looks sufficiently like a path.

The HLD trick

Well, what can we do to improve it? This trick is really the same — find the son w of v that has the maximum |T_w|, add s_v to H_w and make it H_v; then, DFS through the rest of T_v and complete the trie H_v as in the slow solution. The trick resembles HLD a lot, since we're basically remembering tries on HLD-paths.

If v is a leaf, of course, we can just create H_v that consists of one vertex.

How do we "add" v to a trie H_w of its son w? Well, v should be the root of the trie afterwards and the original H_w's root should become its son, so we're rerooting H_w. We'll just create a new vertex in H_w with s_v in it, make it the root of H_w and make the previous root of H_w its son. And if we number the tries somehow, then we can just set the number of H_v to be the number of H_w.

It remains true that dif(v) is |H_v| — the number of vertices in the trie H_v, which allows us to compute those values directly. After computing dif(v) for each v, we can just compute both statistics directly in O(N).

Since each vertex of T corresponds to vertices in at most tries (for each heavy edge that's on the path from it to the root), we aren't creating tries with a total of O(N²) vertices, but 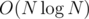. The time complexity is therefore 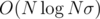. However, the same is true for the memory, so you can't waste it too much!

Bonus: you have an additional tiebreaker condition for vertices with identical . Count the number of distinct strings which occurred exactly k times for each k in an array P_r[]; take the vertex/vertices with lexicograhically maximum P_r[] (as many strings as possible which occur only once, etc).

Bonus 2: Can you get rid of the logarithm in the time complexity?