Этот раунд был немного необычным: некоторые из задач были ранее подготовлены студентами и сотрудниками Саратовского ГУ для прошедших олимпиад, одна из задач была подготовлена участником dalex для одного из регулярных (неучебных) раундов Codeforces, но не использована там.
Отсортируем массив по невозрастанию. Тогда ответом на задачу будет несколько первых флешек. Будем идти по массиву слева направо пока не наберем сумму m. Количество взятых элементов и будет ответом на задачу.
Асимптотическая сложность решения: O(nlogn).
Пусть cnti — количество книг i-го жанра. Тогда ответом на задачу будет величина равная 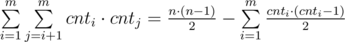 . В первой сумме мы считаем непосредственно количество хороших пар книг, а во втором из общего количества пар книг вычитаем количество плохих пар.
. В первой сумме мы считаем непосредственно количество хороших пар книг, а во втором из общего количества пар книг вычитаем количество плохих пар.
Асимптотическая сложность решения: O(n + m2) или O(n + m).
Пусть s — сумма элементов массива. Если число s делится на n, то сбалансированный массив будет состоять из n чисел  . В этом случае разность между минимальным и максимальным будет равна 0. Легко видеть, что в любом другом случае ответ будет больше 0. С другой стороны массив, состоящий из
. В этом случае разность между минимальным и максимальным будет равна 0. Легко видеть, что в любом другом случае ответ будет больше 0. С другой стороны массив, состоящий из 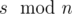 чисел
чисел 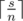 и
и 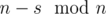 чисел
чисел 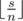 является сбалансированным с разницей минимального и максимального равной 1. Обозначим этот сбалансированный массив b. Чтобы получить массив b давайте сначала отсортируем массив a по невозрастанию, а после этого попарно сопоставим элементы массивов a, b друг другу. Таким образом некоторые числа в a придется увеличить до соответствующих чисел в b, а некоторые уменьшить. Поскольку за одну операцию мы сразу уменьшаем где-то значение, а где-то увеличиваем, то ответ равен
является сбалансированным с разницей минимального и максимального равной 1. Обозначим этот сбалансированный массив b. Чтобы получить массив b давайте сначала отсортируем массив a по невозрастанию, а после этого попарно сопоставим элементы массивов a, b друг другу. Таким образом некоторые числа в a придется увеличить до соответствующих чисел в b, а некоторые уменьшить. Поскольку за одну операцию мы сразу уменьшаем где-то значение, а где-то увеличиваем, то ответ равен 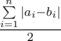 .
.
Асимптотическая сложность решения: O(nlogn).
609D - Гаджеты за доллары и фунты
Заметим, что если Нура может купить k гаджетов за x дней то за x + 1 день она тоже сможет их купить. Таким образом, функция возможности покупки является монотонной. Значит, мы можем найти минимальный день с помощью бинарного поиска. Пусть lf = 0 — левая граница бинарного поиска, а rg = n + 1 — правая. Будем поддерживать инвариант, что в левой границе мы не можем купить k гаджетов, а в правой можем (будем считать, что в n + 1 день мы гаджеты стоят 0). Теперь зафиксируем некоторый день d и поймем можем ли мы купить k гаджетов за d дней. Введем функцию f(d), которая равна 1, если мы можем купить k гаджетов за d дней и 0 в противном случае. Каждый раз в качестве d будем выбирать значение 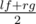 . Если f(d) = 1, то нужно двигать правую границу бинарного поиска rg = d, иначе левую lf = d. По завершении бинарного поиска нужно проверить если lf = n + 1, то ответ - 1, иначе ответ равен lf. Для вычисления функции f(d) предварительно образуем 2 массива стоимостей гаджетов, продающихся за доллары и фунты, и отсортируем их. Теперь заметим, что мы можем покупать гаджеты за доллары в день i ≤ d когда доллар стоит меньше всего и день j ≤ d, когда фунт стоит меньше всего. Пусть теперь мы хотим купить x гаджетов за доллары и соответственно k - x за фунты. Конечно мы будем покупать самые дешевые из них (для этого мы и отсортировали заранее массивы). Будем перебирать x от 0 до k и одновременно поддерживать сумму стоимостей долларовых гаджетов s1 и фунтовых s2. Для x = 0 эту сумму легко посчитать за O(k), для всех остальных x эту сумму можно пересчитать за O(1) из суммы для x - 1 добавлением очередного долларового гаджета и выкидываением фунтового.
. Если f(d) = 1, то нужно двигать правую границу бинарного поиска rg = d, иначе левую lf = d. По завершении бинарного поиска нужно проверить если lf = n + 1, то ответ - 1, иначе ответ равен lf. Для вычисления функции f(d) предварительно образуем 2 массива стоимостей гаджетов, продающихся за доллары и фунты, и отсортируем их. Теперь заметим, что мы можем покупать гаджеты за доллары в день i ≤ d когда доллар стоит меньше всего и день j ≤ d, когда фунт стоит меньше всего. Пусть теперь мы хотим купить x гаджетов за доллары и соответственно k - x за фунты. Конечно мы будем покупать самые дешевые из них (для этого мы и отсортировали заранее массивы). Будем перебирать x от 0 до k и одновременно поддерживать сумму стоимостей долларовых гаджетов s1 и фунтовых s2. Для x = 0 эту сумму легко посчитать за O(k), для всех остальных x эту сумму можно пересчитать за O(1) из суммы для x - 1 добавлением очередного долларового гаджета и выкидываением фунтового.
Асимптотическая сложность решения: O(klogn).
609E - Минимальное остовное дерево по каждому ребру
Задача была предложена участником dalex.
Эта задача является очень стандартной задачей на знание минимальных покрывающих деревьев и умение построить некоторую структуру данных на дереве, для вычисления некоторой функции. Построим любое минимальное покрывающее дерево любым быстрым алгоритмом (например алгоритмом Краскала). Для всех ребер вошедших в MST мы уже нашли ответ — это просто вес MST. Теперь рассмотрим любое другое ребро (x, y). В MST существует единственный простой путь от вершины x к вершине y. Найдем на этом пути самое длинное ребро, выкинем его и добавим ребро (x, y). Согласно критерию Тарьяна, получившееся дерево является минимальным покрывающим, содержащим ребро (x, y) (это не является утверждением критерия Тарьяна, но из него следует).
Теперь рассмотрим техническую сторону решения. Для того, чтобы быстро находить самое длинное ребро на пути между двумя вершинами в дереве подвесим дерево за любую вершину (например за первую). Теперь обозначим l = lca(x, y) — наименьший общий предок вершин (x, y). lca(x, y) можно искать с помощью метода двоичного подъема, одновременно поддерживая самое тяжелое ребро.
Конечно такую задачу можно решать и более сложными структурами данных, например с помощью Heavy-light decomposition или Linkcut tree.
Асимптотическая сложность решения: O(mlogn).
В этой задаче нужно было реализовать все, что написано в условии, но за хорошую асимпотику. Будем поддерживать множество пока не съеденных комаров (например с помощью set} в C++ или TreeSet в Java) и обрабатывать приземления комаров по очереди. Также будем поддерживать множество отрезков (ai, bi), где ai — положение i-й лягушки, а bi = ai + li, где li — длина языка i-й лягушки. Пусть очередной комар приземлился в точке x. Выберем среди отрезков (ai, bi) отрезок с минимальным ai таким, что bi ≥ x. Если окажется, что ai ≤ x, то этот отрезок и будет соответствовать лягушке, которая съест комара. Иначе комара никто не съест и его нужно добавить в множество несъеденных. Если комара съест i-я лягушка, то нужно удлинить её язык на размер комара и обновить отрезок (ai, bi) в структуре данных. После этого нужно в множестве несъеденных комаров брать ближайшего к лягушке справа и если возможно есть этого комара (это можно сделать с помощью например метода lower_bound в C++). Возможно лягушка сможет съесть несколько комаров, в этом случае их нужно по очереди есть.
Отрезки (ai, bi) можно хранить например в динамическом дереве отрезков по правому концу bi, а значениями хранить ai. Либо то же самое можно делать с помощью декартова дерева. Но это слишком сложно можно написать более простое решение. Будем хранить в обычном дереве отрезков для каждого левого конца ai (левые концы не меняются никогда) правый конец bi. Теперь можно например бинарным поиском найти минимальный префикс максимум на котором больше либо равен x. В этом случае получаем решение за O(nlog2n). Но это решение можно улучшить. Для этого нужно просто спускаться по дереву отрезков: если в левой половине максимум больше либо равен x идем влево иначе вправо.
Асимптотическая сложность решения: O((n + m)log(n + m)).







