608A - Saitama Destroys Hotel
Author: ed1d1a8d
The minimum amount of time required is the maximum value of ti + fi and s, where t_i and f_i are the time and the floor of the passenger respectively.
The initial observation that should be made for this problem is that only the latest passenger on each floor matters. So, we can ignore all passengers that aren't the latest passenger on each floor.
Now, assume there is only a passenger on floor s. Call this passenger a. The time taken for this passenger is clearly ta + fa (the time taken to wait for the passenger summed to the time taken for the elevator to reach the bottom).
Now, add in one passenger on a floor lower than s. Call this new passenger b. There are 2 possibilities for this passenger. Either the elevator reaches the passenger's floor after the passenger's time of arrival or the elevator reaches the passenger's floor before the passenger's time of arrival. For the first case, no time is added to the solution, and the solution remains ta + fa. For the second case, the passenger on floor s doesn't matter, and the time taken is tb + fb for the new passenger.
The only thing left is to determine whether the elevator reaches the new passenger before ti of the new passenger. It does so if ta + (fa - fb) > tb. Clearly this is equivalent to whether ta + fa > tb + fb. Thus, the solution is max of max(ta + fa, tb + fb).
A similar line of reasoning can be applied to the rest of the passengers. Thus, the solution is the maximum value of ti + fi and s.
608B - Hamming Distance Sum
Author: ed1d1a8d
We are trying to find 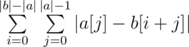 . Swapping the sums, we see that this is equivalent to
. Swapping the sums, we see that this is equivalent to 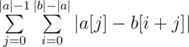 .
.
Summing up the answer in the naive fashion will give an O(n2) solution. However, notice that we can actually find 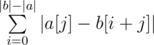 without going through each individual character. Rather, all we need is a frequency count of different characters. To obtain this frequency count, we can simply build prefix count arrays of all characters on b. Let's call this prefix count array F, where F[x][c] gives the number of occurrences of the character c in the prefix [0, x) of b. We can then write
without going through each individual character. Rather, all we need is a frequency count of different characters. To obtain this frequency count, we can simply build prefix count arrays of all characters on b. Let's call this prefix count array F, where F[x][c] gives the number of occurrences of the character c in the prefix [0, x) of b. We can then write 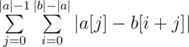 . as
. as 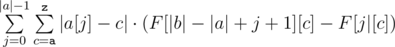 . This gives us a linear solution.
. This gives us a linear solution.
Time Complexity — O(|a| + |b|), Memory Complexity — O(|b|)
608C - Chain Reaction
Author: Chilli
We can solve this problem using dynamic programming. Let dp[x] be the minimum number of objects destroyed in the range [0, x] given that position x is unaffected by an explosion. We can compute dp[x] using the following recurrence:
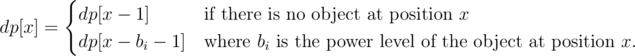
Now, if we can place an object to the right of all objects with any power level, we can destroy some suffix of the (sorted list of) objects. The answer is thus the minimum number of objects destroyed given that we destroy some suffix of the objects first. This can be easily evaluated as
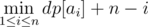
Time Complexity — O(max(ai)), Memory Complexity — O(max(ai))






