Hi Codeforces,
Can anybody help me with the following problem ?
Reduced Problem Statement
Given 2 integers N and K. We are asked to print the lexographically smallest permutation of first N natural number such that abs(i - posi) ≥ K for every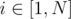 
if it exists where posi is the position of ith element in the permutation.
Constraints:
1 ≤ N ≤ 105 0 ≤ K ≤ N - 1
Example
Input: 3 2 2 3 0 3 1
Output: -1 1 2 3 2 3 1
Explanation
For the first test case, N = 2 and K = 2. It is impossible to permute [1, 2] in any way such that abs(P[1]-1) >= 2 and abs(P[2]-2) >= 2. Hence, output is -1.
For the second test case, N = 3 and K = 0. We can just set P[i] = i, and hence the answer is 1 2 3 For the third case, the valid permutations are [2, 3, 1] and [3, 1, 2]. The answer is [2, 3, 1] since it is lexicographically smaller than [3, 1, 2].
