620A - Professor GukiZ's Robot

Легко видеть, что ответ в задаче равен max(|x₁ - x₂|, |y₁ - y₂|).

С++ solution

Сложность: O(1).

620B - Grandfather Dovlet’s calculator

В этой задаче достаточно было пройти по всем числам от a до b и прибавить к ответу количество сегментов, необходимое для отображения очередного числа. Для подсчёта этой величины нужно пройти по всем десятичным цифрам числа и прибавить к ответу количество сегментов, необходимой для отображения очередной цифры. Последние величины можно просто посчитать по картинке и вбить в один массив.

C++ solution

Сложность: O((b - a)logb).

620C - Pearls in a Row

Будем решать задачу жадно. Давайте набирать жемчужинки в самый левый хороший подотрезок по одному, начиная с первой жемчужинки. Как только подотрезок станет хорошим (то есть встретится повторение) начнём набирать новый хороший подотрезок. Если мы не смогли набрать ни одного хорошего подотрезка, то ответ  - 1. В противном случае, в конце массива может остаться некоторое количество различных элементов, их нужно отнести к последнему набранному отрезку. Легко доказать, что такая жадность правильная: нужно рассмотреть первые два отрезка в оптимальном ответе и понять, что второй отрезок можно расширить пока первый не станет размера первого подотрезка в нашем ответе.

C++ solution

Сложность: O(nlogn).

620D - Professor GukiZ and Two Arrays

Случаи когда нужно сделать одну операцию или их не нужно делать вовсе легко разобрать в лоб (за O(nm)). Теперь рассмотрим случай когда нужно сделать две операции. Заметим, что можно считать, что после двух операций два элемента первого массива перейдёт во второй массив и наоборот, поскольку в противном случае то же самое можно сделать и за одну операцию и значит мы уже рассмотрели этот случай. Давайте переберём пару чисел, которая перейдёт во второй массив и сложим суммы в некоторую структуру данных (например, можно сложить в map в C++). Далее переберём пару чисел во втором массиве b_i, b_j и найдём в нашей структуре данных сумму v наиболее близкую к числу x = s_a - s_b + 2·(b[i] + b[j]) и обновим ответ значением |x - v|. Нужную сумму можно искать бинарным поиском по структуре данных (для map есть функция lower_bound).

C++ solution

Сложность: O((n² + m²)log(n + m)).

620E - New Year Tree

Запустим dfs из корня дерева и выпишем вершины в порядке в котором их обойдёт dfs (эта перестановка называется обходом Эйлера). Легко видеть, что поддерево в этой перестановке является подотрезком. Заметим, что цветов всего 60, таким образом, мы можем хранить множество цветов просто как маску двоичных битов в 64-битном типе (*long long* в C++, long в Java). Построим дерево отрезков над Эйлеровым обходом, который поддерживает операцию покраски подотрезка и нахождения маски цветов на подотрезке.

С++ solution

Сложность: O(nlogn).

620F - Xors on Segments

В этой задаче неудачно были подобраны ограничения в связи с чем некоторые участники сдали решения со сложностью O(n² + m).

Заметим сначала, что 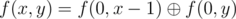. Значения f(0, x) можно было просто предподсчитать или заметить что в зависимости от остатка числа x по модулю 4 значение функции равно x, 1, x + 1, 0 соответственно.

Воспользуемся алгоритмом Мо. Разобьём все запросы на блоков по левому концу. Внутри каждого блока отсортируем запросы по правому концу. Пусть r наибольшая левая граница внутри блока, тогда все левые границы отстоят от r на расстояние не более чем , а правые границы идут в порядке неубывания, поэтому их можно двигать по одному (в сумме на один блок мы сделаем не более n передвижений правой границы). Передвигая правую границу, внутри блока для чисел в позициях от r + 1 до текущей правой границы будем поддерживать два бора: первый для значений f(0, x - 1), второй для значений f(0, x), в первом будем поддерживать наименьшее значение x, во втором — наибольшее. Понятно как добавлять число в боры, после добавлений нужно найти наибольшее значение, которое может образовать текущий x для этого будем спускаться по первому бору, поддерживая инвариант того, что в текущем поддереве минимальное значение не больше x, и по возможности ходить по биту отличному от нашего. Аналогичное нужно делать во втором боре, только нужно поддерживать инвариант, что максимальное значение не меньше x. После того как для текущего запроса мы сдвинули правую границу на сколько нужно, нужно пройти от левой границы запроса до r и, не добавляя значения в бор, обновить ответы. Ещё отдельно для каждого запроса в новом (пустом) боре нужно пройти от левой границы до r добавляя значения в бор и обновляя ответ.

С++ solution: в коде 0-й бор соответсвует второму, а 1-й — первому.

Сложность: 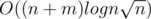.