<h4>Aim — To multiply $2$ $n$-degree polynomials in $O(n*\log n)$ instead of the trivial $O(n^2)$</h4>↵
↵
<i>I have poked around a lot of resources to understand FFT (fast fourier transform), but the math behind it would intimidate me and I would never really try to learn it. Finally last week I learned it from some pdfs and CLRS by building up an intuition of what is actually happening in the algorithm.↵
Using this article I intend to clarify the concept to myself and bring all that I read under one article which would be simple to understand and help others struggling with fft.↵
</i>↵
↵
Let’s get started $\rightarrow$ <br>↵
$\displaystyle A(x) = \sum_{i = 0}^{n - 1} a_i*x^i, B(x) = \sum_{i = 0}^{n - 1} b_i*x^i, C(x) = A(x) * B(x)$ <br>↵
Here $A(x)$ and $B(x)$ are polynomials of degree $n-1$. Now we want to retrieve $C(x)$ in $O(n*\log n)$↵
↵
So our methodology would be this $\rightarrow$ <br>↵
<ol>↵
<li>Convert $A(x)$ and $B(x)$ from coefficient form to point value form. (FFT)↵
<li>Now do the $O(n)$ convolution in point value form to obtain $C(x)$ in point value form, i.e. basically $C(x) = A(x) * B(x)$ in point value form.↵
<li>Now convert $C(x)$ from point value from to coefficient form (Inverse FFT).↵
</ol>↵
↵
↵
Q) What is point value form ? <br>↵
Ans) Well, a polynomial $A(x)$ of degree n can be represented in its point value form like this $\rightarrow$↵
$ A(x) = {(x_0, y_0), (x_1, y_1), (x_2, y_2), \dots, (x_{n-1}, y_{n-1})}$ , where $y_k = A(x_k)$ and all the $x_k$ are distinct. <br>↵
So basically the first element of the pair is the value of $x$ for which we computed the function and second value in the pair is the value which is computed i.e $A(x_k)$. <br>↵
Also the point value form and coefficient form have a mapping i.e. for each point value form there is exactly one coefficient representation, if for $k$ degree polynomial, $k+1$ point value forms have been used at least. <br>↵
Reason is simple, the point value form has $n$ variables i.e, $a_0,a_1, \dots, a_{n-1} $ and $n$ equations i.e. $y_0 = A(x_0), y_1 = A(x_1), \dots, y_{n-1} = A(x_{n-1})$ so only one solution is there. <br>↵
Now using matrix multiplication the conversion from coefficient form to point value form for the polynomial $\displaystyle A(x) = \sum_{i = 0}^{n-1} a_i*x^i$ can be shown like this $\rightarrow$ <br><br>↵
$\begin{pmatrix}1 & x_0 & x_0^{2} & ... & x_0^{n - 1} \\ 1 & x_1 & x_1^{2} & ... & x_1^{n - 1} \\ ... & ... & ... & ... & ... \\ 1 & x_{n - 1} & x_{n - 1}^{2} & ... & x_{n - 1}^{n - 1} \\ \end{pmatrix}$↵
$\begin{pmatrix}a_0\\ a_1\\ ...\\ a_{n - 1} \\ \end{pmatrix}$↵
$ = \begin{pmatrix}y_0\\ y_1\\ ...\\ y_{n - 1}\\ \end{pmatrix} -(1)$↵
<br><br>↵
And the inverse, that is the conversion from point value form to coefficient form for the same polynomial can be shown as this ↵
$\rightarrow$ <br><br>↵
$\begin{pmatrix}1 & x_0 & x_0^{2} & ... & x_0^{n - 1} \\ 1 & x_1 & x_1^{2} & ... & x_1^{n - 1} \\ ... & ... & ... & ... & ... \\ 1 & x_{n - 1} & x_{n - 1}^{2} & ... & x_{n - 1}^{n - 1} \\ \end{pmatrix}^{-1}$↵
$\begin{pmatrix}y_0\\ y_1\\ ...\\ y_{n - 1}\\ \end{pmatrix} $↵
$ = \begin{pmatrix}a_0\\ a_1\\ ...\\ a_{n - 1} \\ \end{pmatrix} -(2)$ ↵
<br><br>↵
Now, let's assume $A(x) = x^{2} + x + 1 = {(1, 3), (2, 7), (3, 13)}$ and $B(x) = x^{2} - 3 = {(1, -2), (2, 1), (3, 6)}$, where degree of $A(x)$ and $B(x) = 2$ <br>↵
Now as $C(x) = A(x) * B(x) = x^{4} + x^{3} - 2x^{2} - 3x - 3$ <br>↵
$C(1) = A(1) * B(1) = 3 * -2 = -6, C(2) = A(2) * B(2) = 7*1 = 7, C(3) = A(3) * B(3) = 13*6 = 78$ <br>↵
↵
So $C(x) = {(1, -6), (2, 7), (3, 78)}$ where degree of $C(x) = $degree of $A(x) + $degree of $B(x) = 4$ <br>↵
But we know that a polynomial of degree $n-1$ requires $n$ point value pairs, so $3$ pairs of $C(x)$ are not sufficient for determining $C(x)$ uniquely as it is a polynomial of degree $4$. <br>↵
Therefore we need to calculate $A(x)$ and $B(x)$, for $2n$ point value pairs instead of $n$ point value pairs so that $C(x)$’s point value form contains $2n$ pairs which would be sufficient to uniquely determine $C(x)$ which would have a degree of $2(n - 1)$.↵
↵
<h5>Now if we had performed this algorithm <b>naively</b> it would have gone on like this $\rightarrow$ </h5>↵
↵
<b>Note — This is NOT the actual FFT algorithm but I would say that understanding this would layout framework to the real thing.<br>↵
Note — This is actually DFT algorithm, ie. Discrete fourier transform.</b>↵
↵
<ol>↵
<li>We construct the point value form of $A(x)$ and $B(x)$ using $x_0, x_1, \dots, x_{2n - 1}$ which can be made using random distinct integers.↵
So point value form of $A(x) ={(x_0, \alpha_0), (x_1, \alpha_1), (x_2, \alpha_2), ..., (x_{2n-1}, \alpha_{2n-1})}$↵
and $B(x) ={(x0, \beta_0), (x1, \beta_1), (x2, \beta_2), ..., (x2n-1, \beta_{2n-1})} -(1)$↵
Note — The $x_0, x_1, \dots, x_{2n-1}$ should be same for $A(x)$ and $B(x)$.↵
This conversion takes $O(n^2)$.↵
↵
<li>As $C(x) = A(x) * B(x)$, then what would have been the point-value form of $C(x)$ ? <br>↵
If we plug in $x_0$ to all $3$ equations then we see that $\rightarrow$ <br>↵
$C(x_0) = A(x_0) * B(x_0)$ <br>↵
$C(x_0) = \alpha_0 * \beta_0 $ <br>↵
So $C(x)$ in point value form will be ↵
$C(x) ={(x_0, \alpha_0*\beta_0), (x_1, \alpha_1*\beta_1), (x_2, \alpha_2*\beta_2), ..., (x_{2n - 1},\alpha_{2n-1}*\beta_{2n-1})}$ <br>↵
This is the convolution, and it’s time complexity is $O(n)$↵
↵
<li>Now converting $C(x)$ back from point value form to coefficient form can be represented by using the equation $2$. Here calculating the inverse of the matrix requires <b>LU decomposition or Lagrange’s Formula</b>. I won’t be going into depth on how to do the inverse, as this wont be required in the REAL FFT. But we get to understand that using Lagrange’s Formula we would’ve been able to do this step in $O(n^2)$.↵
</ol>↵
↵
<b>Note — </b> Here the algorithm was performed wherein we used $x_0, x_1, \dots, x_{2n-1}$ as ordinary real numbers, the FFT on the other hand uses roots of unity instead and we are able to optimize the $O(n^2)$ conversions from coefficient to point value form and vice versa to $O(n*\log n)$ because of the special mathematical properties of roots of unity which allows us to use the divide and conquer approach.<b> I would recommend to stop here and re-read the article till here until the algorithm is crystal clear as this is the raw concept of FFT. </b>↵
↵
<h5><b>A math primer on complex numbers and roots of unity would be a must now. </b> </h5>↵
Q) What is a complex number ? <br>↵
Answer — Quoting Wikipedia, “A complex number is a number that can be expressed in the form $a + bi$, where $a$ and $b$ are real numbers and $i$ is the imaginary unit, that satisfies the equation $i^2 = -1 $. In this expression, $a$ is the real part and $b$ is the imaginary part of the complex number.”↵
The argument of a complex number is equal to the magnitude of the vector from origin $(0, 0)$ to $(a, b)$, therefore $arg(z) = a^2 + b^2$ where $z = a + bi$. <br>↵
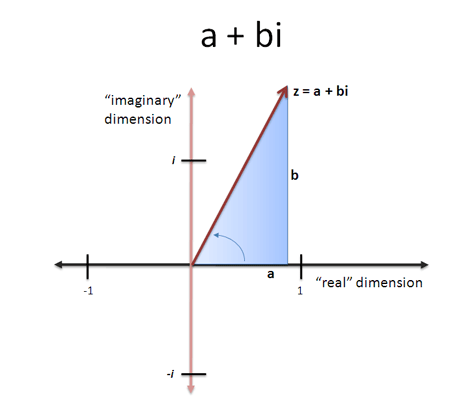 <br>↵
Q) What are the roots of unity ? <br>↵
Answer — An $n$th root of unity, where $n$ is a positive integer (i.e. $n = 1, 2, 3, \dots$), is a number $z$ satisfying the equation $z^n = 1$.↵
 <br>↵
In the image above, n = 2, n = 3, n = 4, from LEFT to RIGHT. <br>↵
Intuitively, we can see that the nth root of unity lies on the circle of radius 1 unit (as its argument is equal to 1) and they are symmetrically placed ie. they are the vertices of a n — sided regular polygon.↵
↵
The $n$ complex $n$th roots of unity can be represented as $e^{2\piik/n}$ for $k = 0, 1, \dots, n - 1$ <br>↵
Also $e^{i\theta}= cos(\theta) + i*sin(\theta) \rightarrow$ Graphically see the roots of unity in a circle then this is quite intuitive.↵
↵
If $n = 4$, then the $4$ roots of unity would’ve been $e^{2\pii * 0/n}, e^{2\pii * 1/n}, e^{2\pii * 2/n}, e^{2\pii * 3/n} = (e^{2\pii/n})^{0}, (e^{2\pii/n})^{1}, (e^{2\pii/n/})^{2}, (e^{2\pii/n})^{3}$ where n should be substituted by 4. <br>↵
Now we notice that all the roots are actually power of $e^{2\pii/n}$.↵
So we can now represent the $n$ complex $n$th roots of unity by $w_{n}^{0}, w_{n}^{1}, w_{n}^{2}, \dots, w_{n}^{n - 1}$, where $w_n = e^{2\pii/n}$ ↵
↵
Now let us prove some lemmas before proceeding further $\rightarrow$↵
↵
<b> Note — Please try to prove these lemmas yourself before you look up at the solution :) </b>↵
↵
<b> Lemma 1 — </b>↵
For any integer $n \geq 0, k \geq 0$ and $d \geq 0$, $w_{dn}^{dk} = w_{n}^{k}$ <br><br>↵
Proof — $w_{dn}^{dk}= (e^{2\pii/dn})^dk = (e^{2\pii/n})^k = w_{n}^{k} $↵
↵
↵
<b> Lemma 2 — </b>↵
For any even integer $n > 0, w_{n}^{n/2} = w_{2} = -1$ <br><br>↵
Proof — $w_{n}^{n/2} = w_{2*(n/2)}^{n/2} = w_{d*2}^{d*1}$ where $d = n / 2$ <br><br>↵
$w_{d*2}^{d*1} = w_{2}^{1}$ — (Using Lemma 1) <br><br>↵
$w_{2}^{1}=e^{i\pi} = cos(\pi) + i * sin(\pi) = -1 + 0 = -1$↵
↵
↵
<b> Lemma 3 — </b>↵
If $n > 0$ is even, then the squares of the n complex nth roots of unity are the (n/2) complex (n/2)th roots of unity, formally ↵
$(w_{n}^{k})^{2} = (w_{n}^{k + n/2})^{2} = w_{n/2}^{k}$ <br><br>↵
Proof — By using lemma 1 we have $(w_{n}^{k})^{2} = w_{2*(n/2)}^{2k} = w_{n/2}^{k}$, for any non-negative integer $k$. Note that if we square all the complex nth roots of unity, then we obtain each (n/2)th root of unity exactly twice since, <br><br>↵
$(w_{n}^{k})^{2} = w_{n/2}^{k} \rightarrow $ (Proved above) <br><br>↵
Also, $(w_{n}^{k + n/2})^{2} = w_{n}^{2k + n} = e^{2\pii*k'/n}$, where $k' = 2k + n$ <br><br>↵
$e^{2\pii*k'/n} = e^{2\pii*(2k + n)/n} = e^{2\pii*(2k/n + 1)} = e^{(2\pii*2k/n) + (2\pii)} = e^{2\pii * 2k/n}*e^{2\pii} = w_{n}^{2k}*(cos(2\pi) + i*sin(2\pi))$ <br><br>↵
$w_{n}^{2k}*(cos(2\pi) + i*sin(2\pi)) = w_{n}^{2k}*1 = w_{n/2}^{k} \rightarrow $ (Proved above) <br><br>↵
Therefore, $(w_{n}^{k})^{2}= (w_{n}^{k + n/2})^{2} = w_{n/2}^{k}$↵
↵
↵
<b> Lemma 4 — </b>↵
For any integer $n \geq 0, k \geq 0, w_{n}^{k + n/2} = -w_{n}^{k}$ <br><br>↵
Proof — $w_{n}^{k + n/2} = e^{2\pii * (k + n/2)/n} =e^{2\pii * (k/n + 1/2)} = e^{(2\pii*k/n) + (\pii)} = e^{2\pii*k/n}*e^{\pii} = w_{n}^{k}*(cos(\pi) + i*sin(\pi)) = w_{n}^{k}*(-1)= -w_{n}^{k}$↵
↵
<h4>1. The FFT — Converting from coefficient form to point value form</h4>↵
Note — Let us assume that we have to multiply $2$ $n$ — degree polynomials, when $n$ is a power of $2$. If $n$ is not a power of $2$, then make it a power of $2$ by padding the polynomial's higher degree coefficients with zeroes. <br>↵
Now we will see how is $A(x)$ converted from coefficient form to point value form in $O(n*\log n)$ using the special properties of n complex nth roots of unity.↵
↵
$y_k = A(x_k)$ <br>↵
$\displaystyle y_k = A(w_{n}^{k}) = \sum_{j = 0}^{n - 1}a_{j}*w_{n}^{kj}$↵
↵
Let us define $\rightarrow$ <br><br>↵
$A^{even}(x) = a_{0} + a_{2}*x + a_{4}*x^{2} + \dots + a_{n-2}*x^{n/2 - 1}, A^{odd}(x) = a_{1} + a_{3}*x + a_{5}*x^{2} + \dots + a_{n-1}*x^{n/2-1}$ <br><br>↵
Here, $A^{even}(x)$ contains all even-indexed coefficients of $A(x)$ and $A^{odd}(x)$ contains all odd-indexed coefficients of $A(x)$. <br><br>↵
It follows that $A(x) = A^{even}(x^{2}) + x*A^{odd}(x^{2})$ <br><br>↵
So now the problem of evaluating $A(x)$ at the n complex nth roots of unity, ie. at $w_{n}^{0}, w_{n}^{1}, \dots, w_{n}^{n - 1}$ reduces to $\rightarrow$↵
↵
<ol>↵
<li> Evaluating the n/2 degree polynomials $A^{even}(x^{2})$ and $A^{odd}(x^{2})$. As $A(x)$ requires $w_{n}^{0}, w_{n}^{1}, \dots, w_{n}^{n - 1}$ as the points on which the function is evaluated. <br><br>↵
Therefore $A(x^{2})$ would’ve required $(w_{n}^{0})^{2}, (w_{n}^{1})^{2}, \dots, (w_{n}^{n - 1})^{2}$. <br><br>↵
Extending this logic to $A^{even}(x^{2})$ and $A^{odd}(x^{2})$ we can say that the $A^{even}(x^{2})$ and $A^{odd}(x^{2})$ would require $(w_{n}^{0})^{2}, (w_{n}^{1})^{2}, \dots, (w_{n}^{n /2 - 1})^{2} \equiv w_{n/2}^{0}, w_{n/2}^{1}, \dots, w_{n/2}^{n/2-1}$ as the points on which they should be evaluated. <br><br>↵
Here we can clearly see that evaluating $A^{even}(x^{2})$ and $A^{odd}(x^{2})$ at $w_{n/2}^{0}, w_{n/2}^{1}, \dots, w_{n/2}^{n/2-1}$ is recursively solving the exact same form as that of the original problem, i.e. evaluating $A(x)$ at $w_{n}^{0}, w_{n}^{1}, \dots, w_{n}^{n - 1}$. (The division part in the divide and conquer algorithm)<br><br>↵
↵
<li> Combining these results using the equation $A(x) = A^{even}(x^{2}) + x*A^{odd}(x^{2})$. (The conquer part in the divide and conquer algorithm). <br><br>↵
Now, $A(w_{n}^{k}) = A^{even}(w_{n}^{2k}) + w_{n}^{k}*A^{odd}(w_{n}^{2k})$, if $k < n/2$, quite straightforward <br><br>↵
And if $k \geq n/2$, then $A(w_{n}^{k}) = A^{even}(w_{n/2}^{k-n/2}) - w_{n}^{k-n/2}*A^{odd}(w_{n/2}^{k - n/2})$ <br><br>↵
Proof — $A(w_{n}^{k}) = A^{even}(w_{n}^{2k}) + w_{n}^{k}*A^{odd}(w_{n}^{2k}) = A^{even}(w_{n/2}^{k}) + w_{n}^{k}*A^{odd}(w_{n/2}^{k})$ using $(w_{n}^{k})^{2} = w_{n/2}^{k}$ <br><br>↵
$A(w_{n}^{k}) = A^{even}(w_{n/2}^{k}) - w_{n}^{k-n/2}*A^{odd}(w_{n/2}^{k})$ using $w_{n}^{k' + n/2} = -w_{n}^{k'}$ i.e. (Lemma 4), where $k' = k - n/2$. <br>↵
</ol>↵
↵
So the pseudocode (Taken from CLRS) for FFT would be like this $\rightarrow$ <br>↵
↵
1.RECURSIVE-FFT(a) <br>↵
2. $n = a$.length() <br>↵
3. If $n == 1$ then return $a$ //Base Case <br>↵
4. $w_{n} = e^{2\pii/n}$ <br>↵
5. $w = 1$ <br>↵
6. $a^{even} = (a_{0}, a_{2}, \dots, a_{n - 2})$ <br>↵
7. $a^{odd} = (a_{1}, a_{3}, \dots, a_{n - 1})$ <br>↵
8. $y^{even} = RECURSIVE-FFT(a^{even})$ <br>↵
9. $y^{odd} = RECURSIVE-FFT(a^{odd})$ <br>↵
10. For $k = 0$ to $n/2 - 1$ <br>↵
11. $y_{k} = y_{k}^{even} + w*y_{k}^{odd}$ <br>↵
12. $y_{k + n/2} = y_{k}^{even} - w*y_{k}^{odd}$ <br>↵
13. $w *= w_{n}$ <br>↵
14. return y; <br>↵
↵
<h4>2. The Multiplication OR Convolution </h4>↵
This is simply this $\rightarrow$ <br>↵
1.a = RECURSIVE-FFT(a), b = RECURSIVE-FFT(b) //Doing the fft. <br>↵
2.For $k = 0$ to $n - 1$ <br>↵
3. $c(k) = a(k) * b(k)$ //Doing the convolution in O(n) <br>↵
↵
<h4>3. The Inverse FFT </h4>↵
Now we have to recover c(x) from point value form to coefficient form and we are done.↵
Well, here I am back after like 8 months, sorry for the trouble.↵
So the whole FFT process can be show like the matrix $\rightarrow$ <br><br>↵
↵
$\begin{pmatrix}1 & 1 & 1 & ... & 1 \\ 1 & w_n & w_n^{2} & ... & w_n^{n - 1} \\ 1 & w_n^{2} & w_n^{4} & ... & w_n^{2(n - 1)} \\ ... & ... & ... & ... & ... \\ 1 & w_n^{n - 1} & w_n^{2(n - 1)} & ... & w_n^{(n - 1)(n - 1)} \\ \end{pmatrix}$↵
$\begin{pmatrix}a_0\\ a_1\\ a_2 \\ ...\\ a_{n - 1} \\ \end{pmatrix}$↵
$ = \begin{pmatrix}y_0\\ y_1\\ y_2 \\ ...\\ y_{n - 1}\\ \end{pmatrix}$↵
↵
<br>The square matrix on the left is the Vandermonde Matrix $(V_n)$, where the $(k, j)$ entry of $V_n$ is $w_n^{kj}$↵
<br>Now for finding the inverse we can write the above equation as $\rightarrow$ <br><br>↵
↵
$\begin{pmatrix}1 & 1 & 1 & ... & 1 \\ 1 & w_n & w_n^{2} & ... & w_n^{n - 1} \\ 1 & w_n^{2} & w_n^{4} & ... & w_n^{2(n - 1)} \\ ... & ... & ... & ... & ... \\ 1 & w_n^{n - 1} & w_n^{2(n - 1)} & ... & w_n^{(n - 1)(n - 1)} \\ \end{pmatrix}^{-1}$↵
$\begin{pmatrix}y_0\\ y_1\\ y_2 \\ ...\\ y_{n - 1}\\ \end{pmatrix} $↵
$ = \begin{pmatrix}a_0\\ a_1\\ a_2 \\ ...\\ a_{n - 1} \\ \end{pmatrix}$ ↵
↵
<br>Now if we can find $V_n^{-1}$ and figure out the symmetry in it like in case of FFT which enables us to solve it in NlogN then we can pretty much do the inverse FFT like the FFT. Given below are Lemma 5 and Lemma 6, where in Lemma 6 shows what $V_n^{-1}$ is by using Lemma 5 as a result.↵
<br><br>↵
↵
<b> Lemma 5 — </b>↵
For $n \geq 1$ and nonzero integer $k$ not a multiple of $n$, $\displaystyle \sum_{j = 0}^{n - 1} (w_n^{k})^{j}$ $ = 0$<br><br> ↵
Proof — $\displaystyle \sum_{j = 0}^{n - 1} (w_n^{k})^{j} = ((w_n^{k})^{n} - 1) / (w_n^{k} - 1) \rightarrow $ Sum of a G.P of $n$ terms.<br>↵
$\displaystyle \sum_{j = 0}^{n - 1} (w_n^{k})^{j} = ((w_n^{n})^{k} - 1) / (w_n^{k} - 1) = ((1)^k - 1) / (w_n^{k} - 1) = 0$ <br><br>↵
We required that $k$ is not a multiple of $n$ because $w_n^{k} = 1$ only when $k$ is a multiple of $n$, so to ensure that the denominator is not 0 we required this constraint.↵
<br><br>↵
<b> Lemma 6 — </b>↵
For $j, k = 0, 1, ..., n - 1,$ the $(j, k)$ entry of $V_n^{-1}$ is $w_n^{-kj} / n$<br><br>↵
Proof — We show that $V_n^{-1} * V_n = I_n$, the $n*n$ identity matrix. Consider the $(j, j')$ entry of $V_n^{-1} * V_n$ and let it be denoted by $[V_n^{-1} * V_n]_{jj'}$↵
<br> So now $\rightarrow$ <br>↵
$\displaystyle [V_n^{-1} * V_n]_{jj'} = \sum_{k = 0}^{n - 1} (w_n^{-kj/n}) * (w_n^{kj'}) = \sum_{k = 0}^{n - 1} w_n^{k(j' - j)} / n$↵
<br><br>↵
Now if $j' = j$ then $w_n^{k(j' - j)} = w_n^{0} = 1$ so the summation becomes 1, otherwise it is 0 in accordance with Lemma 5 given above. Note here that the constraints fore Lemma 5 are satisfied here as $n \geq 1$ and $j' - j$ cannot be a multiple of $n$ as $j' \neq j$ in this case and the maximum and minimum possible value of $j' - j$ is $(n - 1)$ and $-(n - 1)$ respectively.↵
<br><br>So now we have it proven that the $(j, k)$ entry of $V_n^{-1}$ is $w_n^{-kj} / n$.↵
<br><br>Therefore, $\displaystyle a_k = (\sum_{j = 0}^{n - 1} y_j * w_n^{-kj}) / n$↵
<br>The above equation is similar to the FFT equation $\rightarrow \displaystyle y_k = \sum_{j = 0}^{n - 1}a_{j}*w_{n}^{kj}$↵
<br><br> The only differences are that $a$ and $y$ are swapped, we have replaced $w_n$ by $w_n^{-1}$ and divided each element of the result by $n$↵
<br> Therefore as rightly said by Adamant that for inverse FFT instead of the roots we use the conjugate of the roots and divide the results by n.↵
<br><br>That is it folks. The inverse FFT might seem a bit hazy in terms of its implementation but it is just similar to the actual FFT with those slight changes and I have shown as to how we come up with those slight changes. In near future I would be writing a follow up article covering the implementation and problems related to FFT.↵
<br><br>↵
[Part 2 is here](http://mirror.codeforces.com/blog/entry/48798)↵
↵
References used — Introduction to Algorithms(By CLRS) and Wikipedia↵
<br><br>Feedback would be appreciated. Also please notify in the comments about any typos and formatting errors :)↵
↵
<i>I have poked around a lot of resources to understand FFT (fast fourier transform), but the math behind it would intimidate me and I would never really try to learn it. Finally last week I learned it from some pdfs and CLRS by building up an intuition of what is actually happening in the algorithm.↵
Using this article I intend to clarify the concept to myself and bring all that I read under one article which would be simple to understand and help others struggling with fft.↵
</i>↵
↵
Let’s get started $\rightarrow$ <br>↵
$\displaystyle A(x) = \sum_{i = 0}^{n - 1} a_i*x^i, B(x) = \sum_{i = 0}^{n - 1} b_i*x^i, C(x) = A(x) * B(x)$ <br>↵
Here $A(x)$ and $B(x)$ are polynomials of degree $n-1$. Now we want to retrieve $C(x)$ in $O(n*\log n)$↵
↵
So our methodology would be this $\rightarrow$ <br>↵
<ol>↵
<li>Convert $A(x)$ and $B(x)$ from coefficient form to point value form. (FFT)↵
<li>Now do the $O(n)$ convolution in point value form to obtain $C(x)$ in point value form, i.e. basically $C(x) = A(x) * B(x)$ in point value form.↵
<li>Now convert $C(x)$ from point value from to coefficient form (Inverse FFT).↵
</ol>↵
↵
↵
Q) What is point value form ? <br>↵
Ans) Well, a polynomial $A(x)$ of degree n can be represented in its point value form like this $\rightarrow$↵
$ A(x) = {(x_0, y_0), (x_1, y_1), (x_2, y_2), \dots, (x_{n-1}, y_{n-1})}$ , where $y_k = A(x_k)$ and all the $x_k$ are distinct. <br>↵
So basically the first element of the pair is the value of $x$ for which we computed the function and second value in the pair is the value which is computed i.e $A(x_k)$. <br>↵
Also the point value form and coefficient form have a mapping i.e. for each point value form there is exactly one coefficient representation, if for $k$ degree polynomial, $k+1$ point value forms have been used at least. <br>↵
Reason is simple, the point value form has $n$ variables i.e, $a_0,a_1, \dots, a_{n-1} $ and $n$ equations i.e. $y_0 = A(x_0), y_1 = A(x_1), \dots, y_{n-1} = A(x_{n-1})$ so only one solution is there. <br>↵
Now using matrix multiplication the conversion from coefficient form to point value form for the polynomial $\displaystyle A(x) = \sum_{i = 0}^{n-1} a_i*x^i$ can be shown like this $\rightarrow$ <br><br>↵
$\begin{pmatrix}1 & x_0 & x_0^{2} & ... & x_0^{n - 1} \\ 1 & x_1 & x_1^{2} & ... & x_1^{n - 1} \\ ... & ... & ... & ... & ... \\ 1 & x_{n - 1} & x_{n - 1}^{2} & ... & x_{n - 1}^{n - 1} \\ \end{pmatrix}$↵
$\begin{pmatrix}a_0\\ a_1\\ ...\\ a_{n - 1} \\ \end{pmatrix}$↵
$ = \begin{pmatrix}y_0\\ y_1\\ ...\\ y_{n - 1}\\ \end{pmatrix} -(1)$↵
<br><br>↵
And the inverse, that is the conversion from point value form to coefficient form for the same polynomial can be shown as this ↵
$\rightarrow$ <br><br>↵
$\begin{pmatrix}1 & x_0 & x_0^{2} & ... & x_0^{n - 1} \\ 1 & x_1 & x_1^{2} & ... & x_1^{n - 1} \\ ... & ... & ... & ... & ... \\ 1 & x_{n - 1} & x_{n - 1}^{2} & ... & x_{n - 1}^{n - 1} \\ \end{pmatrix}^{-1}$↵
$\begin{pmatrix}y_0\\ y_1\\ ...\\ y_{n - 1}\\ \end{pmatrix} $↵
$ = \begin{pmatrix}a_0\\ a_1\\ ...\\ a_{n - 1} \\ \end{pmatrix} -(2)$ ↵
<br><br>↵
Now, let's assume $A(x) = x^{2} + x + 1 = {(1, 3), (2, 7), (3, 13)}$ and $B(x) = x^{2} - 3 = {(1, -2), (2, 1), (3, 6)}$, where degree of $A(x)$ and $B(x) = 2$ <br>↵
Now as $C(x) = A(x) * B(x) = x^{4} + x^{3} - 2x^{2} - 3x - 3$ <br>↵
$C(1) = A(1) * B(1) = 3 * -2 = -6, C(2) = A(2) * B(2) = 7*1 = 7, C(3) = A(3) * B(3) = 13*6 = 78$ <br>↵
↵
So $C(x) = {(1, -6), (2, 7), (3, 78)}$ where degree of $C(x) = $degree of $A(x) + $degree of $B(x) = 4$ <br>↵
But we know that a polynomial of degree $n-1$ requires $n$ point value pairs, so $3$ pairs of $C(x)$ are not sufficient for determining $C(x)$ uniquely as it is a polynomial of degree $4$. <br>↵
Therefore we need to calculate $A(x)$ and $B(x)$, for $2n$ point value pairs instead of $n$ point value pairs so that $C(x)$’s point value form contains $2n$ pairs which would be sufficient to uniquely determine $C(x)$ which would have a degree of $2(n - 1)$.↵
↵
<h5>Now if we had performed this algorithm <b>naively</b> it would have gone on like this $\rightarrow$ </h5>↵
↵
<b>Note — This is NOT the actual FFT algorithm but I would say that understanding this would layout framework to the real thing.<br>↵
Note — This is actually DFT algorithm, ie. Discrete fourier transform.</b>↵
↵
<ol>↵
<li>We construct the point value form of $A(x)$ and $B(x)$ using $x_0, x_1, \dots, x_{2n - 1}$ which can be made using random distinct integers.↵
So point value form of $A(x) ={(x_0, \alpha_0), (x_1, \alpha_1), (x_2, \alpha_2), ..., (x_{2n-1}, \alpha_{2n-1})}$↵
and $B(x) ={(x0, \beta_0), (x1, \beta_1), (x2, \beta_2), ..., (x2n-1, \beta_{2n-1})} -(1)$↵
Note — The $x_0, x_1, \dots, x_{2n-1}$ should be same for $A(x)$ and $B(x)$.↵
This conversion takes $O(n^2)$.↵
↵
<li>As $C(x) = A(x) * B(x)$, then what would have been the point-value form of $C(x)$ ? <br>↵
If we plug in $x_0$ to all $3$ equations then we see that $\rightarrow$ <br>↵
$C(x_0) = A(x_0) * B(x_0)$ <br>↵
$C(x_0) = \alpha_0 * \beta_0 $ <br>↵
So $C(x)$ in point value form will be ↵
$C(x) ={(x_0, \alpha_0*\beta_0), (x_1, \alpha_1*\beta_1), (x_2, \alpha_2*\beta_2), ..., (x_{2n - 1},\alpha_{2n-1}*\beta_{2n-1})}$ <br>↵
This is the convolution, and it’s time complexity is $O(n)$↵
↵
<li>Now converting $C(x)$ back from point value form to coefficient form can be represented by using the equation $2$. Here calculating the inverse of the matrix requires <b>LU decomposition or Lagrange’s Formula</b>. I won’t be going into depth on how to do the inverse, as this wont be required in the REAL FFT. But we get to understand that using Lagrange’s Formula we would’ve been able to do this step in $O(n^2)$.↵
</ol>↵
↵
<b>Note — </b> Here the algorithm was performed wherein we used $x_0, x_1, \dots, x_{2n-1}$ as ordinary real numbers, the FFT on the other hand uses roots of unity instead and we are able to optimize the $O(n^2)$ conversions from coefficient to point value form and vice versa to $O(n*\log n)$ because of the special mathematical properties of roots of unity which allows us to use the divide and conquer approach.<b> I would recommend to stop here and re-read the article till here until the algorithm is crystal clear as this is the raw concept of FFT. </b>↵
↵
<h5><b>A math primer on complex numbers and roots of unity would be a must now. </b> </h5>↵
Q) What is a complex number ? <br>↵
Answer — Quoting Wikipedia, “A complex number is a number that can be expressed in the form $a + bi$, where $a$ and $b$ are real numbers and $i$ is the imaginary unit, that satisfies the equation $i^2 = -1 $. In this expression, $a$ is the real part and $b$ is the imaginary part of the complex number.”↵
The argument of a complex number is equal to the magnitude of the vector from origin $(0, 0)$ to $(a, b)$, therefore $arg(z) = a^2 + b^2$ where $z = a + bi$. <br>↵
 <br>↵
Q) What are the roots of unity ? <br>↵
Answer — An $n$th root of unity, where $n$ is a positive integer (i.e. $n = 1, 2, 3, \dots$), is a number $z$ satisfying the equation $z^n = 1$.↵
 <br>↵
In the image above, n = 2, n = 3, n = 4, from LEFT to RIGHT. <br>↵
Intuitively, we can see that the nth root of unity lies on the circle of radius 1 unit (as its argument is equal to 1) and they are symmetrically placed ie. they are the vertices of a n — sided regular polygon.↵
↵
The $n$ complex $n$th roots of unity can be represented as $e^{2\piik/n}$ for $k = 0, 1, \dots, n - 1$ <br>↵
Also $e^{i\theta}= cos(\theta) + i*sin(\theta) \rightarrow$ Graphically see the roots of unity in a circle then this is quite intuitive.↵
↵
If $n = 4$, then the $4$ roots of unity would’ve been $e^{2\pii * 0/n}, e^{2\pii * 1/n}, e^{2\pii * 2/n}, e^{2\pii * 3/n} = (e^{2\pii/n})^{0}, (e^{2\pii/n})^{1}, (e^{2\pii/n/})^{2}, (e^{2\pii/n})^{3}$ where n should be substituted by 4. <br>↵
Now we notice that all the roots are actually power of $e^{2\pii/n}$.↵
So we can now represent the $n$ complex $n$th roots of unity by $w_{n}^{0}, w_{n}^{1}, w_{n}^{2}, \dots, w_{n}^{n - 1}$, where $w_n = e^{2\pii/n}$ ↵
↵
Now let us prove some lemmas before proceeding further $\rightarrow$↵
↵
<b> Note — Please try to prove these lemmas yourself before you look up at the solution :) </b>↵
↵
<b> Lemma 1 — </b>↵
For any integer $n \geq 0, k \geq 0$ and $d \geq 0$, $w_{dn}^{dk} = w_{n}^{k}$ <br><br>↵
Proof — $w_{dn}^{dk}= (e^{2\pii/dn})^dk = (e^{2\pii/n})^k = w_{n}^{k} $↵
↵
↵
<b> Lemma 2 — </b>↵
For any even integer $n > 0, w_{n}^{n/2} = w_{2} = -1$ <br><br>↵
Proof — $w_{n}^{n/2} = w_{2*(n/2)}^{n/2} = w_{d*2}^{d*1}$ where $d = n / 2$ <br><br>↵
$w_{d*2}^{d*1} = w_{2}^{1}$ — (Using Lemma 1) <br><br>↵
$w_{2}^{1}=e^{i\pi} = cos(\pi) + i * sin(\pi) = -1 + 0 = -1$↵
↵
↵
<b> Lemma 3 — </b>↵
If $n > 0$ is even, then the squares of the n complex nth roots of unity are the (n/2) complex (n/2)th roots of unity, formally ↵
$(w_{n}^{k})^{2} = (w_{n}^{k + n/2})^{2} = w_{n/2}^{k}$ <br><br>↵
Proof — By using lemma 1 we have $(w_{n}^{k})^{2} = w_{2*(n/2)}^{2k} = w_{n/2}^{k}$, for any non-negative integer $k$. Note that if we square all the complex nth roots of unity, then we obtain each (n/2)th root of unity exactly twice since, <br><br>↵
$(w_{n}^{k})^{2} = w_{n/2}^{k} \rightarrow $ (Proved above) <br><br>↵
Also, $(w_{n}^{k + n/2})^{2} = w_{n}^{2k + n} = e^{2\pii*k'/n}$, where $k' = 2k + n$ <br><br>↵
$e^{2\pii*k'/n} = e^{2\pii*(2k + n)/n} = e^{2\pii*(2k/n + 1)} = e^{(2\pii*2k/n) + (2\pii)} = e^{2\pii * 2k/n}*e^{2\pii} = w_{n}^{2k}*(cos(2\pi) + i*sin(2\pi))$ <br><br>↵
$w_{n}^{2k}*(cos(2\pi) + i*sin(2\pi)) = w_{n}^{2k}*1 = w_{n/2}^{k} \rightarrow $ (Proved above) <br><br>↵
Therefore, $(w_{n}^{k})^{2}= (w_{n}^{k + n/2})^{2} = w_{n/2}^{k}$↵
↵
↵
<b> Lemma 4 — </b>↵
For any integer $n \geq 0, k \geq 0, w_{n}^{k + n/2} = -w_{n}^{k}$ <br><br>↵
Proof — $w_{n}^{k + n/2} = e^{2\pii * (k + n/2)/n} =e^{2\pii * (k/n + 1/2)} = e^{(2\pii*k/n) + (\pii)} = e^{2\pii*k/n}*e^{\pii} = w_{n}^{k}*(cos(\pi) + i*sin(\pi)) = w_{n}^{k}*(-1)= -w_{n}^{k}$↵
↵
<h4>1. The FFT — Converting from coefficient form to point value form</h4>↵
Note — Let us assume that we have to multiply $2$ $n$ — degree polynomials, when $n$ is a power of $2$. If $n$ is not a power of $2$, then make it a power of $2$ by padding the polynomial's higher degree coefficients with zeroes. <br>↵
Now we will see how is $A(x)$ converted from coefficient form to point value form in $O(n*\log n)$ using the special properties of n complex nth roots of unity.↵
↵
$y_k = A(x_k)$ <br>↵
$\displaystyle y_k = A(w_{n}^{k}) = \sum_{j = 0}^{n - 1}a_{j}*w_{n}^{kj}$↵
↵
Let us define $\rightarrow$ <br><br>↵
$A^{even}(x) = a_{0} + a_{2}*x + a_{4}*x^{2} + \dots + a_{n-2}*x^{n/2 - 1}, A^{odd}(x) = a_{1} + a_{3}*x + a_{5}*x^{2} + \dots + a_{n-1}*x^{n/2-1}$ <br><br>↵
Here, $A^{even}(x)$ contains all even-indexed coefficients of $A(x)$ and $A^{odd}(x)$ contains all odd-indexed coefficients of $A(x)$. <br><br>↵
It follows that $A(x) = A^{even}(x^{2}) + x*A^{odd}(x^{2})$ <br><br>↵
So now the problem of evaluating $A(x)$ at the n complex nth roots of unity, ie. at $w_{n}^{0}, w_{n}^{1}, \dots, w_{n}^{n - 1}$ reduces to $\rightarrow$↵
↵
<ol>↵
<li> Evaluating the n/2 degree polynomials $A^{even}(x^{2})$ and $A^{odd}(x^{2})$. As $A(x)$ requires $w_{n}^{0}, w_{n}^{1}, \dots, w_{n}^{n - 1}$ as the points on which the function is evaluated. <br><br>↵
Therefore $A(x^{2})$ would’ve required $(w_{n}^{0})^{2}, (w_{n}^{1})^{2}, \dots, (w_{n}^{n - 1})^{2}$. <br><br>↵
Extending this logic to $A^{even}(x^{2})$ and $A^{odd}(x^{2})$ we can say that the $A^{even}(x^{2})$ and $A^{odd}(x^{2})$ would require $(w_{n}^{0})^{2}, (w_{n}^{1})^{2}, \dots, (w_{n}^{n /2 - 1})^{2} \equiv w_{n/2}^{0}, w_{n/2}^{1}, \dots, w_{n/2}^{n/2-1}$ as the points on which they should be evaluated. <br><br>↵
Here we can clearly see that evaluating $A^{even}(x^{2})$ and $A^{odd}(x^{2})$ at $w_{n/2}^{0}, w_{n/2}^{1}, \dots, w_{n/2}^{n/2-1}$ is recursively solving the exact same form as that of the original problem, i.e. evaluating $A(x)$ at $w_{n}^{0}, w_{n}^{1}, \dots, w_{n}^{n - 1}$. (The division part in the divide and conquer algorithm)<br><br>↵
↵
<li> Combining these results using the equation $A(x) = A^{even}(x^{2}) + x*A^{odd}(x^{2})$. (The conquer part in the divide and conquer algorithm). <br><br>↵
Now, $A(w_{n}^{k}) = A^{even}(w_{n}^{2k}) + w_{n}^{k}*A^{odd}(w_{n}^{2k})$, if $k < n/2$, quite straightforward <br><br>↵
And if $k \geq n/2$, then $A(w_{n}^{k}) = A^{even}(w_{n/2}^{k-n/2}) - w_{n}^{k-n/2}*A^{odd}(w_{n/2}^{k - n/2})$ <br><br>↵
Proof — $A(w_{n}^{k}) = A^{even}(w_{n}^{2k}) + w_{n}^{k}*A^{odd}(w_{n}^{2k}) = A^{even}(w_{n/2}^{k}) + w_{n}^{k}*A^{odd}(w_{n/2}^{k})$ using $(w_{n}^{k})^{2} = w_{n/2}^{k}$ <br><br>↵
$A(w_{n}^{k}) = A^{even}(w_{n/2}^{k}) - w_{n}^{k-n/2}*A^{odd}(w_{n/2}^{k})$ using $w_{n}^{k' + n/2} = -w_{n}^{k'}$ i.e. (Lemma 4), where $k' = k - n/2$. <br>↵
</ol>↵
↵
So the pseudocode (Taken from CLRS) for FFT would be like this $\rightarrow$ <br>↵
↵
1.RECURSIVE-FFT(a) <br>↵
2. $n = a$.length() <br>↵
3. If $n == 1$ then return $a$ //Base Case <br>↵
4. $w_{n} = e^{2\pii/n}$ <br>↵
5. $w = 1$ <br>↵
6. $a^{even} = (a_{0}, a_{2}, \dots, a_{n - 2})$ <br>↵
7. $a^{odd} = (a_{1}, a_{3}, \dots, a_{n - 1})$ <br>↵
8. $y^{even} = RECURSIVE-FFT(a^{even})$ <br>↵
9. $y^{odd} = RECURSIVE-FFT(a^{odd})$ <br>↵
10. For $k = 0$ to $n/2 - 1$ <br>↵
11. $y_{k} = y_{k}^{even} + w*y_{k}^{odd}$ <br>↵
12. $y_{k + n/2} = y_{k}^{even} - w*y_{k}^{odd}$ <br>↵
13. $w *= w_{n}$ <br>↵
14. return y; <br>↵
↵
<h4>2. The Multiplication OR Convolution </h4>↵
This is simply this $\rightarrow$ <br>↵
1.a = RECURSIVE-FFT(a), b = RECURSIVE-FFT(b) //Doing the fft. <br>↵
2.For $k = 0$ to $n - 1$ <br>↵
3. $c(k) = a(k) * b(k)$ //Doing the convolution in O(n) <br>↵
↵
<h4>3. The Inverse FFT </h4>↵
Now we have to recover c(x) from point value form to coefficient form and we are done.↵
Well, here I am back after like 8 months, sorry for the trouble.↵
So the whole FFT process can be show like the matrix $\rightarrow$ <br><br>↵
↵
$\begin{pmatrix}1 & 1 & 1 & ... & 1 \\ 1 & w_n & w_n^{2} & ... & w_n^{n - 1} \\ 1 & w_n^{2} & w_n^{4} & ... & w_n^{2(n - 1)} \\ ... & ... & ... & ... & ... \\ 1 & w_n^{n - 1} & w_n^{2(n - 1)} & ... & w_n^{(n - 1)(n - 1)} \\ \end{pmatrix}$↵
$\begin{pmatrix}a_0\\ a_1\\ a_2 \\ ...\\ a_{n - 1} \\ \end{pmatrix}$↵
$ = \begin{pmatrix}y_0\\ y_1\\ y_2 \\ ...\\ y_{n - 1}\\ \end{pmatrix}$↵
↵
<br>The square matrix on the left is the Vandermonde Matrix $(V_n)$, where the $(k, j)$ entry of $V_n$ is $w_n^{kj}$↵
<br>Now for finding the inverse we can write the above equation as $\rightarrow$ <br><br>↵
↵
$\begin{pmatrix}1 & 1 & 1 & ... & 1 \\ 1 & w_n & w_n^{2} & ... & w_n^{n - 1} \\ 1 & w_n^{2} & w_n^{4} & ... & w_n^{2(n - 1)} \\ ... & ... & ... & ... & ... \\ 1 & w_n^{n - 1} & w_n^{2(n - 1)} & ... & w_n^{(n - 1)(n - 1)} \\ \end{pmatrix}^{-1}$↵
$\begin{pmatrix}y_0\\ y_1\\ y_2 \\ ...\\ y_{n - 1}\\ \end{pmatrix} $↵
$ = \begin{pmatrix}a_0\\ a_1\\ a_2 \\ ...\\ a_{n - 1} \\ \end{pmatrix}$ ↵
↵
<br>Now if we can find $V_n^{-1}$ and figure out the symmetry in it like in case of FFT which enables us to solve it in NlogN then we can pretty much do the inverse FFT like the FFT. Given below are Lemma 5 and Lemma 6, where in Lemma 6 shows what $V_n^{-1}$ is by using Lemma 5 as a result.↵
<br><br>↵
↵
<b> Lemma 5 — </b>↵
For $n \geq 1$ and nonzero integer $k$ not a multiple of $n$, $\displaystyle \sum_{j = 0}^{n - 1} (w_n^{k})^{j}$ $ = 0$<br><br> ↵
Proof — $\displaystyle \sum_{j = 0}^{n - 1} (w_n^{k})^{j} = ((w_n^{k})^{n} - 1) / (w_n^{k} - 1) \rightarrow $ Sum of a G.P of $n$ terms.<br>↵
$\displaystyle \sum_{j = 0}^{n - 1} (w_n^{k})^{j} = ((w_n^{n})^{k} - 1) / (w_n^{k} - 1) = ((1)^k - 1) / (w_n^{k} - 1) = 0$ <br><br>↵
We required that $k$ is not a multiple of $n$ because $w_n^{k} = 1$ only when $k$ is a multiple of $n$, so to ensure that the denominator is not 0 we required this constraint.↵
<br><br>↵
<b> Lemma 6 — </b>↵
For $j, k = 0, 1, ..., n - 1,$ the $(j, k)$ entry of $V_n^{-1}$ is $w_n^{-kj} / n$<br><br>↵
Proof — We show that $V_n^{-1} * V_n = I_n$, the $n*n$ identity matrix. Consider the $(j, j')$ entry of $V_n^{-1} * V_n$ and let it be denoted by $[V_n^{-1} * V_n]_{jj'}$↵
<br> So now $\rightarrow$ <br>↵
$\displaystyle [V_n^{-1} * V_n]_{jj'} = \sum_{k = 0}^{n - 1} (w_n^{-kj/n}) * (w_n^{kj'}) = \sum_{k = 0}^{n - 1} w_n^{k(j' - j)} / n$↵
<br><br>↵
Now if $j' = j$ then $w_n^{k(j' - j)} = w_n^{0} = 1$ so the summation becomes 1, otherwise it is 0 in accordance with Lemma 5 given above. Note here that the constraints fore Lemma 5 are satisfied here as $n \geq 1$ and $j' - j$ cannot be a multiple of $n$ as $j' \neq j$ in this case and the maximum and minimum possible value of $j' - j$ is $(n - 1)$ and $-(n - 1)$ respectively.↵
<br><br>So now we have it proven that the $(j, k)$ entry of $V_n^{-1}$ is $w_n^{-kj} / n$.↵
<br><br>Therefore, $\displaystyle a_k = (\sum_{j = 0}^{n - 1} y_j * w_n^{-kj}) / n$↵
<br>The above equation is similar to the FFT equation $\rightarrow \displaystyle y_k = \sum_{j = 0}^{n - 1}a_{j}*w_{n}^{kj}$↵
<br><br> The only differences are that $a$ and $y$ are swapped, we have replaced $w_n$ by $w_n^{-1}$ and divided each element of the result by $n$↵
<br> Therefore as rightly said by Adamant that for inverse FFT instead of the roots we use the conjugate of the roots and divide the results by n.↵
<br><br>That is it folks. The inverse FFT might seem a bit hazy in terms of its implementation but it is just similar to the actual FFT with those slight changes and I have shown as to how we come up with those slight changes. In near future I would be writing a follow up article covering the implementation and problems related to FFT.↵
[Part 2 is here](http://mirror.codeforces.com/blog/entry/48798)↵
↵
References used — Introduction to Algorithms(By CLRS) and Wikipedia↵
<br><br>Feedback would be appreciated. Also please notify in the comments about any typos and formatting errors :)↵





