665A - Автобусы между городами
Задача предложена пользователем unprost.
Рассмотрим интервал времени, когда Симион будет находиться на трассе строго между городами (x1, y1), (x1 = 60h + m, y1 = x1 + ta). Переберём встречный автобус. Пусть (x2, y2) — это интервал времени, когда встречный автобус будет находиться строго между городами. Если пересечение этих интервалов (x = max(x1, x2), y = min(y1, y2)) не пусто, то Симион посчитает этот автобус.
Сложность: O(1).
665B - Покупки
Задачу предложил Ayush Anand JeanValjean01.
В этой задаче нужно было сделать ровно то, что написано в условии. Никаких хитростей и подвохов.
Сложность: O(nmk).
665C - Простые строки
Задачу предложил Zi Song Yeoh zscoder.
Для решения этой задачи есть два подхода: жадность и динамическое программирование.
Первый подход: Рассмотрим некоторый отрезок из подряд идущих одинаковых букв. Пусть длина отрезка k. Очевидно мы должны изменить хотя бы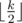 
букв в ней, чтобы не было одинаковых букв подряд. С другой стороны мы можем изменить второй, четвёртый и т.д. символы на букву, которая не равна букве слева и справа от нашего отрезка.
Второй подход: Пусть zka — наименьшее количество изменений, чтобы на префиксе длины k не было двух подряд идущих одинаковых букв и при этом символ s'k был равен букве a. Переберём букву, которую поставим на k + 1-й позиции и если она не равна a сделаем переход. Цена перехода равна 0, если мы поставили ту же букву, что стояла в исходной строке s на k + 1-й позиции. В противном случае цена равна 1.
Сложность: O(n).
665D - Красивое подмножество
Задачу предложил Zi Song Yeoh zscoder.
Рассмотрим подмножество A, являющееся ответом на задачу. Пусть a, b, c — три произвольных элемента из A и пусть не более один из них равен 1. По принципе Дирихле среди этих трёх чисел обязательно найдется пара чисел с одинаковой чётностью. Поскольку в этой паре только одно может быть равно 1, то их сумма чётна и больше 2. Таким образом, такое невозможно. Значит A состоит либо из двух чисел больших единицы (с простой суммой), либо из некоторого количества единиц и возможно одной не единицы (если она равна простому минус один). Первый случай легко обработать за O(n2). Второй случай легко обрабатывается за линейное время. Среди двух ответов, конечно, можно просто выбрать лучший.
Проверять на простоту числа порядка 2·106 за O(1) можно с помощью обычного или линейного решета Эратосфена.
Сложность: O(n2 + X), где X — максимальное среди заданных чисел.
