At first, this solution is more simple than one solution i saw among the comments.

now let's see how to solve this problem.

First we know it just asks the minnium of cost. Obviously we should use DP.

Let F[i] represent the minnium of cost to create the 'A' string which has n characters.

Consider first operation, easily we know F[i] = F[i - 1] + x

How to deal with the second operation and third? We can consider them together!

But why? After thinking about that, we know that we use 'delete operation' when we have excess characters.

However, if we just add 'a', it is impossible to exceed.

The only reason of exceeding is we used the second operation!

After that, we can know 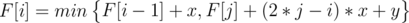E.G. we want aaaaa , we have aaa, so we first copy and paste(cost y), then we have aaaaaa, we have to delete one(cost x)

Particularly,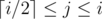

Therefore, it is an O(n²) algorithm. TLE!

We can use humdrum queue to make it much faster. As a result, it is O(n)

#include <bits/stdc++.h>
using namespace std;

#define mp make_pair
#define fi first
#define se second
#define rep(i,s,t) for(int i = s; i <= t; ++ i)
typedef long long LL;
const int MaxN = 10000050;

int N, X, Y;
LL dp[MaxN], Ans = 1LL<<61;
pair<LL,int> Q[MaxN];
int front, tail;

int main()
{
    scanf("%d%d%d",&N,&X,&Y);
    front = 0; tail = -1;
    dp[1] = X; Q[++tail] = mp(3LL*X, 1);
    rep(i,2,N)
    {
        while(front <= tail && Q[front].se < (int)(i/2)+(i%2)) ++ front;
        dp[i] = min(dp[i-1] + X, Q[front].fi + Y - (LL)i*X);
        //f(i)=min{f(i-1)+x, f(j)+2*j*x-i*x+y}
        while(front <= tail && dp[i] + 2LL*i*X < Q[tail].fi) -- tail;
        Q[++tail] = mp(dp[i] + 2LL*i*X, i);
    }
    printf("%I64d",dp[N]);
    return 0;
}

or see my submission here.