We hope everyone enjoyed the problems. Here is the editorial for the problems. I tried to make it more detailed but there might be some parts that might not be explained clearly.↵
↵
[Div. 2 A — Crazy Computer](http://mirror.codeforces.com/contest/716/problem/A)↵
------------------↵
↵
Prerequisites : None↵
↵
This is a straightforward implementation problem. Iterate through the times in order, keeping track of when is the last time a word is typed, keeping a counter for the number of words appearing on the screen. Increment the counter by $1$ whenever you process a new time. Whenever the difference between the time for two consecutive words is greater than $c$, reset the counter to $0$. After that, increment it by $1$. ↵
↵
Time Complexity : $O(n)$, since the times are already sorted.↵
↵
<spoiler summary="Code (O(n))">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<int,int> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int N = 1e5 + 3;↵
ll a[N];↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
int n, c; cin >> n >> c;↵
for(int i = 0; i < n; i++)↵
{↵
cin >> a[i];↵
}↵
//sort(a, a + n);↵
int cnt = 0;↵
for(int i = 0; i < n; i++)↵
{↵
if(i == 0) cnt++;↵
else↵
{↵
if(a[i] - a[i - 1] <= c) cnt++;↵
else cnt = 1;↵
}↵
}↵
cout << cnt;↵
return 0;↵
}↵
~~~~~↵
</spoiler>↵
↵
[Div. 2 B — Complete The Word](http://mirror.codeforces.com/contest/716/problem/B)↵
------------------↵
↵
Prerequisites : None↵
↵
Firstly, if the length of the string is less than $26$, output $-1$ immediately.↵
↵
We want to make a substring of length $26$ have all the letters of the alphabet. Thus, the simplest way is to iterate through all substrings of length $26$ (there are $O(n)$ such substrings), then for each substring count the number of occurrences of each alphabet, ignoring the question marks. After that, if there exist a letter that occurs twice or more, this substring cannot contain all letters of the alphabet, and we process the next substring. Otherwise, we can fill in the question marks with the letters that have not appeared in the substring and obtain a substring of length $26$ which contains all letters of the alphabet. After iterating through all substrings, either there is no solution, or we already created a nice substring. If the former case appears, output $-1$. Otherwise, fill in the remaining question marks with random letters and output the string.↵
↵
Note that one can optimize the solution above by noting that we don't need to iterate through all $26$ letters of each substring we consider, but we can iterate through the substrings from left to right and when we move to the next substring, remove the front letter of the current substring and add the last letter of the next substring. This optimization is not required to pass.↵
↵
We can still optimize it further and make the complexity purely $O(|s|)$. We use the same trick as above, when we move to the next substring, we remove the previous letter and add the new letter. We store a frequency array counting how many times each letter appear in the current substring. Additionally, store a counter which we will use to detect whether the current substring can contain all the letters of the alphabet in $O(1)$. When a letter first appear in the frequency array, increment the counter by $1$. If a letter disappears (is removed) in the frequency array, decrement the counter by $1$. When we add a new question mark, increment the counter by $1$. When we remove a question mark, decrement the counter by $1$. To check whether a substring can work, we just have to check whether the counter is equal to $26$. This solution works in $O(|s|)$.↵
↵
Time Complexity : $O(|s| \cdot 26^{2})$, $O(|s| \cdot 26)$ or $O(|s|)$↵
↵
<spoiler summary="Code (O(26^2*|s|)">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<int,int> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int N = 10000;↵
int cnt[27];↵
string s; int n;↵
↵
bool valid()↵
{↵
for(int i = 0; i < 26; i++)↵
{↵
if(cnt[i] >= 2) return false;↵
}↵
return true;↵
}↵
↵
void fillall()↵
{↵
for(int i = 0; i < n; i++)↵
{↵
if(s[i] == '?') s[i] = 'A';↵
}↵
}↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
cin >> s;↵
n = s.length();↵
if(n < 26) {cout << -1; return 0;}↵
for(int i = 25; i < n; i++)↵
{↵
memset(cnt, 0, sizeof(cnt));↵
for(int j = i; j >= i - 25; j--)↵
{↵
cnt[s[j]-'A']++;↵
}↵
if(valid())↵
{↵
//cout << "GG " << i << '\n';↵
int cur = 0;↵
while(cnt[cur]>0) cur++;↵
for(int j = i - 25; j <= i; j++)↵
{↵
if(s[j] == '?')↵
{↵
s[j] = cur + 'A';↵
cur++;↵
while(cnt[cur]>0) cur++;↵
}↵
}↵
fillall();↵
cout << s;↵
return 0;↵
}↵
}↵
cout << -1;↵
return 0;↵
}↵
~~~~~↵
</spoiler>↵
↵
<spoiler summary="Code (O(26*|s|)">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<int,int> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int N = 10000;↵
int cnt[27];↵
string s; int n;↵
↵
bool valid()↵
{↵
for(int i = 0; i < 26; i++)↵
{↵
if(cnt[i] >= 2) return false;↵
}↵
return true;↵
}↵
↵
void fillall()↵
{↵
for(int i = 0; i < n; i++)↵
{↵
if(s[i] == '?') s[i] = 'A';↵
}↵
}↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
cin >> s;↵
n = s.length();↵
if(n < 26) {cout << -1; return 0;}↵
for(int i = 0; i < 26; i++) cnt[s[i]-'A']++;↵
if(valid())↵
{↵
int cur = 0;↵
while(cnt[cur]>0) cur++;↵
for(int i = 0; i < 26; i++)↵
{↵
if(s[i] == '?')↵
{↵
s[i] = cur + 'A';↵
cur++;↵
while(cnt[cur]>0) cur++;↵
}↵
}↵
fillall();↵
cout << s;↵
return 0;↵
}↵
for(int i = 26; i < n; i++)↵
{↵
cnt[s[i]-'A']++; cnt[s[i-26]-'A']--;↵
if(valid())↵
{↵
//cout << "GG " << i << '\n';↵
int cur = 0;↵
while(cnt[cur]>0) cur++;↵
for(int j = i - 25; j <= i; j++)↵
{↵
if(s[j] == '?')↵
{↵
s[j] = cur + 'A';↵
cur++;↵
while(cnt[cur]>0) cur++;↵
}↵
}↵
fillall();↵
cout << s;↵
return 0;↵
}↵
}↵
cout << -1;↵
return 0;↵
}↵
~~~~~↵
</spoiler>↵
↵
<spoiler summary="Code (O(|s|)">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<int,int> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int N = 50000;↵
int cnt[27];↵
string s; int n;↵
int counter;↵
↵
bool valid()↵
{↵
//cout << counter << endl;↵
return (counter == 26);↵
}↵
↵
void fillall()↵
{↵
for(int i = 0; i < n; i++)↵
{↵
if(s[i] == '?') s[i] = 'A';↵
}↵
}↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
cin >> s;↵
n = s.length();↵
if(n < 26) {cout << -1; return 0;}↵
counter = 0;↵
for(int i = 0; i < 26; i++)↵
{↵
if(s[i] == '?')↵
{↵
counter++; continue;↵
}↵
cnt[s[i]-'A']++;↵
if(cnt[s[i]-'A'] == 1) counter++;↵
}↵
if(valid())↵
{↵
int cur = 0;↵
while(cnt[cur]>0) cur++;↵
for(int i = 0; i < 26; i++)↵
{↵
if(s[i] == '?')↵
{↵
s[i] = cur + 'A';↵
cur++;↵
while(cnt[cur]>0) cur++;↵
}↵
}↵
fillall();↵
cout << s;↵
return 0;↵
}↵
for(int i = 26; i < n; i++)↵
{↵
if(s[i] != '?') {cnt[s[i]-'A']++; if(cnt[s[i]-'A']==1) counter++;}↵
if(s[i-26] != '?') {cnt[s[i-26]-'A']--; if(cnt[s[i-26]-'A']==0) counter--;}↵
if(s[i-26] == '?') counter--;↵
if(s[i] == '?') counter++;↵
if(valid())↵
{↵
int cur = 0;↵
while(cnt[cur]>0) cur++;↵
for(int j = i - 25; j <= i; j++)↵
{↵
if(s[j] == '?')↵
{↵
s[j] = cur + 'A';↵
cur++;↵
while(cnt[cur]>0) cur++;↵
}↵
}↵
fillall();↵
cout << s;↵
return 0;↵
}↵
}↵
cout << -1;↵
return 0;↵
}↵
~~~~~↵
</spoiler>↵
↵
[Div. 2 C/Div. 1 A — Plus and Square Root](http://mirror.codeforces.com/contest/715/problem/A)↵
------------------↵
↵
Prerequisites : None↵
↵
Firstly, let $a_{i} (1 \le i \le n)$ be the number on the screen before we level up from level $i$ to $i + 1$. Thus, we require all the $a_{i}$s to be perfect square and additionally to reach the next $a_{i}$ via pressing the plus button, we require $a_{i + 1} \equiv \sqrt{a_{i}} (mod (i + 1))$ and $a_{i + 1} \ge \sqrt{a_{i}}$ for all $1 \le i < n$. Additionally, we also require $a_{i}$ to be a multiple of $i$. Thus, we just need to construct a sequence of such integers so that the output numbers does not exceed the limit $10^{18}$. ↵
↵
There are many ways to do this. The third sample actually gave a large hint on my approach. If you were to find the values of $a_{i}$ from the second sample, you'll realize that it is equal to $4, 36, 144, 400$. You can try to find the pattern from here. My approach is to use $a_{i} = [i(i + 1)]^{2}$. Clearly, it is a perfect square for all $1 \le i \le n$ and when $n = 100000$, the output values can be checked to be less than $10^{18}$$. Additionally, we also have $a_{i + 1} = [(i + 1)(i + 2)]^2 \equiv i(i + 1) (mod {2}$ which is a multiple of $i + 1$, and $\sqrt{a_{i}} = i(i + 1))$, since both are is also a multiples of $i + 1$.↵
↵
The constraints $a_{i}$ must be a multiple of $i$ was added to make the problem easier for Div. 1 A.↵
↵
Time Complexity : $O(n)$↵
↵
<spoiler summary="Code (O(n))">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<ll,ll> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
ll n; cin >> n;↵
for(ll i = 1; i <= n; i++)↵
{↵
if(i == 1) cout << 2 << '\n';↵
else cout << i*(i+1)*(i+1)-(i-1) << '\n';↵
}↵
return 0;↵
}↵
↵
~~~~~↵
</spoiler>↵
↵
[Div. 2 D/Div. 1 B — Complete The Graph](http://mirror.codeforces.com/contest/715/problem/B)↵
------------------↵
↵
Prerequisites : Dijkstra's Algorithm↵
↵
This problem is actually quite simple if you rule out the impossible conditions. Call the edges that does not have fixed weight variable edges. First, we'll determine when a solution exists.↵
↵
Firstly, we ignore the variable edges. Now, find the length of the shortest path from $s$ to $e$. If this length is $< L$, there is no solution, since even if we replace the $0$ weights with any positive weight the shortest path will never exceed this shortest path. Thus, if the length of this shortest path is $< L$, there is no solution. (If no path exists we treat the length as $\infty$.)↵
↵
Next, we replace the edges with $0$ weight with weight $1$. Clearly, among all the possible graphs you can generate by replacing the weights, this graph will give the minimum possible shortest path from $s$ to $e$, since increasing any weight will not decrease the length of the shortest path. Thus, if the shortest path of this graph is $> L$, there is no solution, since the shortest path will always be $> L$. If no path exists we treat the length as $\infty$.↵
↵
Other than these two conditions, there will always be a way to assign the weights so that the shortest path from $s$ to $e$ is exactly $L$! How do we prove this? First, consider all paths from $s$ to $e$ that has at least one $0$ weight edge, as changing weights won't affect the other paths. Now, we repeat this algorithm. Initially, assign all the weights as $1$. Then, sort the paths in increasing order of length. If the length of the shortest path is equal to $L$, we're done. Otherwise, increase the weight of one of the variable edges on the shortest path by $1$. Note that this will increase the lengths of some of the paths by $1$. It is not hard to see that by repeating these operations the shortest path will eventually have length $L$, so an assignment indeed exists.↵
↵
Now, we still have to find a valid assignment of weights. We can use a similar algorithm as our proof above. Assign $1$ to all variable edges first. Next, we first find and keep track of the shortest path from $s$ to $e$. Note that if this path has no variable edges it must have length exactly $L$ or strictly more than $L$, so either we're already done or the shortest path contains variable edges and the length is strictly less than $L$. (otherwise we're done)↵
↵
From now on, whenever we assign weight to a variable edge (after assigning $1$ to every variable edge), we call the edge assigned.↵
↵
Now, mark all variable edges not on the shortest path we found as $\infty$ weight. (we can choose any number greater than $L$ as $\infty$) Next, we will find the shortest path from $s$ to $e$, and replace the weight of an unassigned variable edge such that the length of the path becomes equal to $L$. Now, we don't touch the assigned edges again. While the shortest path from $s$ to $e$ is still strictly less than $L$, we repeat the process and replace a variable edge that is not assigned such that the path length is equal to $L$. Note that this is always possible, since otherwise this would've been the shortest path in one of the previous steps. Eventually, the shortest path from $s$ to $e$ will have length exactly $L$. It is easy to see that we can repeat this process at most $n$ times because we are only replacing the edges which are on the initial shortest path we found and there are less than $n$ edges to replace (we only touch each edge at most once). Thus, we can find a solution after less than $n$ iterations. So, the complexity becomes $O(mn \log n)$. This is sufficient to pass all tests.↵
↵
What if the constraints were $n, m \le 10^{5}$? Can we do better? ↵
↵
Yes! Thanks to [user:HellKitsune,2016-09-17] who found this solution during testing. First, we rule out the impossible conditions like we did above. Then, we assign all the variable edges with $\infty$ weight. We enumerate the variable edges arbitarily. Now, we binary search to find the minimal value $p$ such that if we make all the variable edges numbered from $1$ to $p$ have weight $1$ and the rest $\infty$, then the shortest path from $s$ to $e$ has length $\le L$. Now, note that if we change the weight of $p$ to $\infty$ the length of shortest path will be more than $L$. (if $p$ equals the number of variable edges, the length of the shortest path is still more than $L$ or it will contradict the impossible conditions) If the weight is $1$, the length of the shortest path is $\le L$. So, if we increase the weight of edge $p$ by $1$ repeatedly, the length of the shortest path from $s$ to $e$ will eventually reach $L$, since this length can increase by at most $1$ in each move. So, since the length of shortest path is non-decreasing when we increase the weight of this edge, we can binary search for the correct weight. This gives an $O(m\log n (\log m + \log L))$ solution.↵
↵
Time Complexity : $O(mn\log n)$ or $O(m\log n (\log m + \log L))$↵
↵
<spoiler summary="Code (O(mnlogn))">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<ll,ll> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int N = 1001;↵
const int M = 10001;↵
const ll INF = ll(1e18);↵
↵
vector<ii> adj[N];↵
vector<int> adj2[N];↵
int L[M]; int R[M];↵
ll d1[N];↵
ll d2[N];↵
int par[N];↵
ll dist[N][N];↵
↵
int n, m, l, s, e;↵
↵
void dijkstra()↵
{↵
d1[s] = 0;↵
priority_queue<ii, vector<ii>, greater<ii> > pq;↵
pq.push(ii(0, s));↵
int cnt = 0;↵
while(!pq.empty())↵
{↵
cnt++;↵
int u = pq.top().se; ll d = pq.top().fi; pq.pop();↵
for(int i = 0; i < adj[u].size(); i++)↵
{↵
int v = adj[u][i].fi; ll w = adj[u][i].se;↵
if(d + w < d1[v])↵
{↵
d1[v] = d + w;↵
pq.push(ii(d1[v], v));↵
}↵
}↵
}↵
cerr << "DIJKSTRA OPERATIONS : " << cnt << '\n';↵
}↵
↵
bool dijkstra2()↵
{↵
d2[s] = 0;↵
priority_queue<ii, vector<ii>, greater<ii> > pq;↵
pq.push(ii(0, s));↵
while(!pq.empty())↵
{↵
int u = pq.top().se; ll d = pq.top().fi; pq.pop();↵
for(int i = 0; i < adj2[u].size(); i++)↵
{↵
int v = adj2[u][i]; ll w = dist[u][v];↵
if(d + abs(w) < d2[v])↵
{↵
d2[v] = d + abs(w);↵
par[v] = u;↵
pq.push(ii(d2[v], v));↵
}↵
}↵
}↵
if(d2[e] > l) return false;↵
int cur = e;↵
while(cur != s)↵
{↵
int p = par[cur];↵
if(dist[p][cur] < 0)↵
{↵
dist[p][cur] = -2; dist[cur][p] = -2;↵
}↵
cur = par[cur];↵
}↵
for(int i = 0; i < n; i++)↵
{↵
for(int j = 0; j < n; j++)↵
{↵
if(dist[i][j] == -1)↵
{↵
dist[i][j] = INF;↵
}↵
}↵
}↵
cur = e;↵
while(cur != s)↵
{↵
int p = par[cur];↵
if(dist[p][cur] < 0)↵
{↵
dist[p][cur] = -1; dist[cur][p] = -1;↵
}↵
cur = par[cur];↵
}↵
return true;↵
}↵
↵
void print()↵
{↵
cout << "YES\n";↵
for(int i = 0; i < m; i++)↵
{↵
int u = L[i]; int v = R[i];↵
ll d = dist[u][v];↵
if(d < 0) d = -d;↵
cout << u << ' ' << v << ' ' << d << '\n';↵
}↵
}↵
↵
bool relax()↵
{↵
for(int i = 0; i < n; i++) d2[i] = INF;↵
memset(par, -1, sizeof(par)); //shouldn't be neccesary↵
d2[s] = 0;↵
priority_queue<ii, vector<ii>, greater<ii> > pq;↵
pq.push(ii(0, s));↵
while(!pq.empty())↵
{↵
int u = pq.top().se; ll d = pq.top().fi; pq.pop();↵
for(int i = 0; i < adj2[u].size(); i++)↵
{↵
int v = adj2[u][i]; ll w = dist[u][v];↵
if(d + abs(w) < d2[v])↵
{↵
d2[v] = d + abs(w);↵
par[v] = u;↵
pq.push(ii(d2[v], v));↵
}↵
}↵
}↵
//cerr << d2[e] << '\n';↵
if(d2[e] == l) return true;↵
int cur = e; bool meet = false;↵
while(cur != s)↵
{↵
int p = par[cur];↵
if(!meet && dist[p][cur] < 0)↵
{↵
ll d = abs(dist[p][cur]);↵
dist[p][cur] = d + l - d2[e];↵
dist[cur][p] = d + l - d2[e];↵
//cerr << d << endl;↵
meet = true;↵
}↵
if(meet) break;↵
cur = par[cur];↵
}↵
return false;↵
}↵
↵
int dist1[N][N];↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
cin >> n >> m >> l >> s >> e;↵
memset(dist1, -1, sizeof(dist1));↵
for(int i = 0; i < m; i++)↵
{↵
int u, v, w; cin >> u >> v >> w;↵
if(w > 0) ↵
{↵
adj[u].pb(ii(v, w)); adj[v].pb(ii(u, w));↵
adj2[u].pb(v); adj2[v].pb(u);↵
dist1[u][v] = w; dist1[v][u] = w;↵
dist[u][v] = w; dist[v][u] = w;↵
}↵
else↵
{↵
adj2[u].pb(v); adj2[v].pb(u);↵
dist[u][v] = -1; dist[v][u] = -1;↵
}↵
L[i] = u; R[i] = v;↵
} ↵
for(int i = 0; i < n; i++)↵
{↵
d1[i] = INF; d2[i] = INF;↵
}↵
dijkstra(); //cerr << d1[e] << '\n';↵
if(d1[e] < l)↵
{↵
cout << "NO\n";↵
return 0;↵
}↵
if(d1[e] == l)↵
{↵
cout << "YES\n";↵
for(int i = 0; i < m; i++)↵
{↵
int u = L[i]; int v = R[i];↵
ll d = dist1[u][v];↵
if(d <= 0) d = INF;↵
cout << u << ' ' << v << ' ' << d << '\n';↵
}↵
return 0;↵
}↵
bool tmp = dijkstra2();↵
if(!tmp)↵
{↵
cout << "NO\n";↵
return 0;↵
}↵
//cerr << d2[e] << '\n';↵
int cnt = 0;↵
while(!relax()) ↵
{↵
relax(); cnt++;↵
}↵
cerr << "RELAXATIONS DONE : " << cnt << '\n';↵
print();↵
}↵
~~~~~↵
</spoiler>↵
↵
<spoiler summary="Code (O(mlogn(logm+logL))">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<ll,ll> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int N = 1001;↵
const int M = 10001;↵
const ll INF = ll(1e18);↵
↵
int n, m, l, s, e;↵
↵
struct edge↵
{↵
int to; ll w; int label;↵
edge(int _to, int _w, int _label){to = _to, w = _w, label = _label;}↵
};↵
↵
int edgecnt = -1;↵
vector<edge> adj[N];↵
ll dist[N];↵
set<ii> used;↵
↵
ll dijk(int p, ll val)↵
{↵
for(int i = 0; i < n; i++) dist[i] = INF;↵
dist[s] = 0;↵
priority_queue<ii, vector<ii>, greater<ii> > pq;↵
pq.push(ii(0, s));↵
while(!pq.empty())↵
{↵
int u = pq.top().se; ll d = pq.top().fi; pq.pop();↵
for(int i = 0; i < adj[u].size(); i++)↵
{↵
edge tmp = adj[u][i];↵
int v = tmp.to; ll w = tmp.w; int lab = tmp.label;↵
if(lab >= 0)↵
{↵
if(lab < p) w = 1;↵
else if(lab == p) w = val;↵
else w = ll(1e14);↵
}↵
if(d + w < dist[v])↵
{↵
dist[v] = d + w;↵
pq.push(ii(dist[v], v));↵
}↵
}↵
}↵
return dist[e];↵
}↵
↵
void setw(int p, ll val)↵
{↵
for(int i = 0; i < n; i++)↵
{↵
for(int j = 0; j < adj[i].size(); j++)↵
{↵
int lab = adj[i][j].label;↵
if(lab >= 0)↵
{↵
if(lab < p)↵
{↵
adj[i][j].w = 1;↵
}↵
else if(lab == p)↵
{↵
adj[i][j].w = val;↵
}↵
else↵
{↵
adj[i][j].w = INF;↵
}↵
}↵
}↵
}↵
}↵
↵
void print()↵
{↵
cout << "YES\n";↵
for(int i = 0; i < n; i++)↵
{↵
for(int j = 0; j < adj[i].size(); j++)↵
{↵
edge tmp = adj[i][j];↵
int v = tmp.to; ll w = tmp.w; ↵
if(used.find(ii(i, v)) == used.end())↵
{↵
cout << i << ' ' << v << ' ' << w << '\n';↵
used.insert(ii(i, v)); used.insert(ii(v, i));↵
}↵
}↵
}↵
}↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
cin >> n >> m >> l >> s >> e;↵
for(int i = 0; i < m; i++)↵
{↵
int u, v, w;↵
cin >> u >> v >> w;↵
int lab = -1;↵
if(w == 0) ↵
{↵
lab = ++edgecnt;↵
}↵
adj[u].pb(edge(v, w, lab));↵
adj[v].pb(edge(u, w, lab));↵
}↵
ll x = dijk(edgecnt, 1); ll y = dijk(-1, 1);↵
if(!(x <= l && l <= y))↵
{↵
cout << "NO\n";↵
return 0;↵
}↵
ll lo = -1; ll hi = edgecnt;↵
ll mid, ans;↵
while(lo <= hi)↵
{↵
mid = (lo+hi)/2;↵
if(dijk(mid, 1) <= l)↵
{↵
ans = mid;↵
hi = mid - 1;↵
}↵
else↵
{↵
lo = mid + 1;↵
}↵
}↵
//now [0..ans] as 1 will give <= L whereas [0..ans - 1] as 1 will give > L↵
if(ans == -1)↵
{↵
setw(-1, 0);↵
print();↵
return 0;↵
}↵
lo = 1; hi = INF;↵
int ans2 = 0;↵
while(lo <= hi)↵
{↵
mid = (lo+hi)>>1;↵
if(dijk(ans, mid) <= l)↵
{↵
ans2 = mid;↵
lo = mid + 1;↵
}↵
else↵
{↵
hi = mid - 1;↵
}↵
}↵
//cerr << ans << ' ' << ans2 << '\n';↵
setw(ans, ans2);↵
print();↵
}↵
~~~~~↵
</spoiler>↵
↵
[Div. 2 E/Div. 1 C — Digit Tree](http://mirror.codeforces.com/contest/715/problem/C)↵
------------------↵
↵
Prerequisites : Tree DP, Centroid Decomposition, Math↵
↵
Compared to the other problems, this one is more standard. The trick is to first solve the problem if we have a fixed vertex $r$ as root and we want to find the number of paths passing through $r$ that works. This can be done with a simple tree dp. For each node $u$, compute the number obtained when going from $r$ down to $u$ and the number obtained when going from $u$ up to $r$, where each number is taken modulo $M$. This can be done with a simple dfs. To calculate the down value, just multiply the value of the parent node by $10$ and add the value on the edge to it. To calculate the up value, we also need to calculate the height of the node. (i.e. the distance from $u$ to $r$) Then, if we let $h$ be the height of $u$, $d$ be the digit on the edge connecting $u$ to its parent and $val$ be the up value of the parent of $u$, then the up value for $u$ is equal to $10^{h - 1} \cdot d + val$. Thus, we can calculate the up and down value for each node with a single dfs.↵
↵
Next, we have to figure out how to combine the up values and down values to find the number of paths passing through $r$ that are divisible by $M$. For this, note that each path is the concatenation of a path from $u$ to $r$ and $r$ to $v$, where $u$ and $v$ are pairs of vertices from different subtrees, and the paths that start from $r$ and end at $r$. For the paths that start and end at $r$ the answer can be easily calculated with the up and down values (just iterate through all nodes as the other endpoint). For the other paths, we iterate through all possible $v$, and find the number of vertices $u$ such that going from $u$ to $v$ will give a multiple of $M$. Since $v$ is fixed, we know its height and down value, which we denote as $h$ and $d$ respectively. So, if the up value of $u$ is equal to $up$, then $up \cdot 10^{h} + d$ must be a multiple of $M$. So, we can solve for $up$ to be $-d \cdot 10^{-h}$ modulo $M$. Note that in this case the multiplicative inverse of $10$ modulo $M$ is well-defined, as we have the condition $\gcd(M, 10) = 1$. To find the multiplicative inverse of $10$, we can find $\phi(M)$ and since by Euler's Formula we have $x^{\phi(M)} \equiv 1 (mod M)$ if $\gcd(x, M) = 1$, we have $x^{\phi(M) - 1} \equiv x^{-1} (mod M)$, which is the multiplicative inverse of $x$ (in this case we have $x = 10$) modulo $M$. After that, finding the $up$ value can be done by binary exponentiation.↵
↵
Thus, we can find the unique value of $up$ such that the path from $u$ to $v$ is a multiple of $M$. This means that we can just use a map to store the up values of all nodes and also the up values for each subtree. Then, to find the number of viable nodes $u$, find the required value of $up$ and subtract the number of suitable nodes that are in the same subtree as $v$ from the total number of suitable nodes. Thus, for each node $v$, we can find the number of suitable nodes $u$ in $O(\log MOD)$ time. ↵
↵
Now, we have to generalize this for the whole tree. We can use centroid decomposition. We pick the centroid as the root $r$ and find the number of paths passing through $r$ as above. Then, the other paths won't pass through $r$, so we can remove $r$ and split the tree into more subtrees, and recursively solve for each subtree as well. Since each subtree is at most half the size of the original tree, and the time taken to solve the problem where the path must pass through the root for a single tree takes time proportional to the size of the tree, this solution works in $O(n \log n(\log n + \log MOD))$ time, where the other $\log n$ comes from using maps.↵
↵
Time Complexity : $O(n \log n(\log n + \log MOD))$↵
↵
<spoiler summary="Code">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<int,int> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int N = 1e5 + 1;↵
const int MAX = 1e9;↵
int MOD, n;↵
↵
bool isprime[100001];↵
vector<ll> primes;↵
vector<ii> adj[N];↵
int subsize[N];↵
bool visited[N];↵
int treesize;↵
vi clrlist;↵
ll up[N];↵
ll down[N];↵
int h[N];↵
int PHI;↵
int dppart[N];↵
↵
ll mult(ll a, ll b)↵
{↵
return (a*b)%MOD;↵
}↵
↵
ll add(ll a, ll b)↵
{↵
return (a+b+MOD)%MOD;↵
}↵
↵
ll modpow(ll a, ll b)↵
{↵
ll r = 1;↵
while(b)↵
{↵
if(b&1) r=(r*a)%MOD;↵
a=(a*a)%MOD;↵
b>>=1;↵
}↵
return r;↵
}↵
↵
void Sieve(int n)↵
{↵
memset(isprime, 1, sizeof(isprime));↵
isprime[1] = false;↵
for(int i = 2; i <= n; i++)↵
{↵
if(isprime[i])↵
{↵
primes.pb(i);↵
for(int j = 2*i; j <= n; j += i)↵
{↵
isprime[j] = false;↵
}↵
}↵
}↵
}↵
↵
int phi(int n)↵
{↵
ll num = 1; ll num2 = n;↵
for(ll i = 0; primes[i]*primes[i] <= n; i++)↵
{↵
if(n%primes[i]==0)↵
{↵
num2/=primes[i];↵
num*=(primes[i]-1);↵
}↵
while(n%primes[i]==0)↵
{↵
n/=primes[i];↵
}↵
}↵
if(n>1)↵
{↵
num2/=n; num*=(n-1);↵
}↵
n = 1;↵
num*=num2;↵
return num;↵
}↵
↵
ll inv(ll a)↵
{↵
return modpow(a, PHI-1);↵
}↵
↵
void dfs(int u, int par)↵
{↵
if(par == -1) clrlist.clear();↵
subsize[u] = 1; clrlist.pb(u);↵
for(int i = 0; i < adj[u].size(); i++)↵
{↵
int v = adj[u][i].fi;↵
if(visited[v]) continue;↵
if(v == par) continue;↵
dfs(v, u);↵
subsize[u] += subsize[v];↵
} ↵
if(par == -1) treesize = subsize[u];↵
}↵
↵
int centroid(int u, int par)↵
{↵
for(int i = 0; i < adj[u].size(); i++)↵
{↵
int v = adj[u][i].fi;↵
if(visited[v]) continue;↵
if(v == par) continue;↵
if(subsize[v]*2 > treesize) return centroid(v, u);↵
}↵
return u;↵
}↵
↵
int parts = 0;↵
void fill(int u, int p, int cent)↵
{↵
if(p == cent)↵
{↵
dppart[u] = parts;↵
parts++;↵
}↵
else if(p != -1)↵
{↵
dppart[u] = dppart[p];↵
}↵
for(int i = 0; i < adj[u].size(); i++)↵
{↵
int v = adj[u][i].fi; int w = adj[u][i].se;↵
if(v == p || visited[v]) continue;↵
down[v] = add(mult(down[u], 10), w);↵
up[v] = add(up[u], mult(modpow(10, h[u]), w));↵
h[v] = h[u] + 1;↵
fill(v, u, cent);↵
//cout << v << ' ' << u << ' ' << up[v] << ' ' << up[u] << '\n';↵
}↵
}↵
↵
ll solve(int cent)↵
{↵
for(int i = 0; i < clrlist.size(); i++)↵
{↵
up[clrlist[i]] = 0; down[clrlist[i]] = 0; h[clrlist[i]] = 0;↵
}↵
parts = 0;↵
fill(cent, -1, cent); parts--;↵
dppart[cent] = -1; ↵
map<ll,ll> tot; //only count up↵
vector<map<ll,ll> > vec; //only count up, but in specific subtree↵
vec.resize(parts+1);↵
tot[0]++;↵
for(int i = 0; i < clrlist.size(); i++)↵
{↵
int u = clrlist[i];↵
//cout << u << ' ' << up[u] << ' ' << down[u] << '\n';↵
if(u == cent) continue;↵
tot[up[u]]++;↵
vec[dppart[u]][up[u]]++;↵
}↵
ll ans = 0;↵
for(int i = 0; i < clrlist.size(); i++)↵
{↵
int u = clrlist[i];↵
int ht = h[u];↵
int pt = dppart[u];↵
if(u == cent)↵
{↵
ans += (tot[0] - 1); //exclude cent as the vertex↵
}↵
else↵
{↵
ll val = ((-down[u])%MOD+MOD)%MOD;↵
val = mult(val, inv(modpow(10, ht)));↵
ans += (tot[val] - vec[pt][val]);↵
}↵
}↵
return ans;↵
}↵
↵
ll compsolve(int u)↵
{↵
dfs(u, -1);↵
int cent = centroid(u, -1);↵
ll ans = solve(cent);↵
//cout << u << ' ' << cent << ' ' << ans << '\n';↵
visited[cent] = true;↵
for(int i = 0; i < adj[cent].size(); i++)↵
{↵
int v = adj[cent][i].fi;↵
if(!visited[v]) ans += compsolve(v);↵
}↵
return ans;↵
}↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
cin >> n >> MOD;↵
if(MOD == 1)↵
{↵
cout << ll(n)*ll(n - 1);↵
return 0;↵
}↵
Sieve(100000); PHI = phi(MOD);↵
for(int i = 0; i < n - 1; i++) //tree is 0-indexed↵
{↵
int u, v, w; cin >> u >> v >> w;↵
adj[u].pb(ii(v, w)); adj[v].pb(ii(u, w));↵
}↵
cout << compsolve(0) << '\n';↵
return 0;↵
}↵
~~~~~↵
</spoiler>↵
↵
[Div. 1 D — Create a Maze](http://mirror.codeforces.com/contest/715/problem/D)↵
------------------↵
↵
Prerequisites : None↵
↵
The solution to this problem is quite simple, if you get the idea. Thanks to [user:dans,2016-09-17] for improving the solution to the current constraints which is much harder than my original proposal.↵
↵
Note that to calculate the difficulty of a given maze, we can just use dp. We write on each square (room) the number of ways to get from the starting square to it, and the number written on $(i, j)$ will be the sum of the numbers written on $(i - 1, j)$ and $(i, j - 1)$, and the edge between $(i - 1, j)$ and $(i, j)$ is blocked, we don't add the number written on $(i - 1, j)$ and similarly for $(i, j - 1)$. We'll call the rooms squares and the doors as edges. We'll call locking doors as edge deletions.↵
↵
First, we look at several attempts that do not work. ↵
↵
Write $t$ in its binary representation. To solve the problem, we just need to know how to construct a maze with difficulty $2x$ and $x + 1$ from a given maze with difficulty $x$. The most direct way to get from $x$ to $2x$ is to increase both dimensions of the maze by $1$. Let's say the bottom right square of the grid was $(n, n)$ and increased to $(n + 1, n + 1)$. So, the number $x$ is written at $(n, n)$. Then, we can block off the edge to the left of $(n + 1, n)$ and above $(n, n + 1)$. This will make the numbers in these two squares equal to $x$, so the number in square $(n + 1, n + 1)$ would be $2x$, as desired. To create $x + 1$ from $x$, we can increase both dimensions by $1$, remove edges such that $(n + 1, n)$ contains $x$ while $(n, n + 1)$ contains $1$ (this requires deleting most of the edges joining the $n$-th column and $(n + 1)$-th column. Thus, the number in $(n, n)$ would be $x + 1$. This would've used way too many edge deletions and the size of the grid would be too large. This was the original proposal.↵
↵
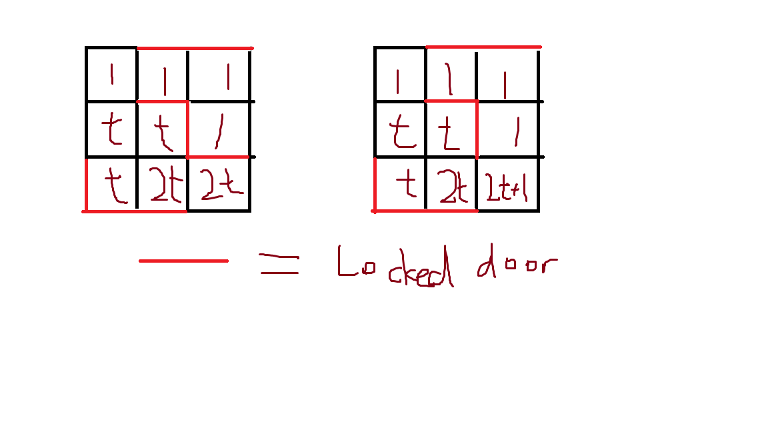
There's another way to do it with binary representation. We construct a grid with difficulty $2x$ and $2x + 1$ from a grid with difficulty $x$. The key idea is to make use of surrounding $1$s and maintaining it with some walls so that $2x + 1$ can be easily constructed. This method is shown in the picture below. This method would've used around $120 \times 120$ grid and $480$ edge deletions, which is too large to pass. ↵
↵
↵
↵
Now, what follows is the AC solution. Since it's quite easy once you get the idea, I recommend you to try again after reading the hint. To read the full solution, click on the spoiler tag.↵
↵
Hint : Binary can't work since there can be up to $60$ binary digits for $t$ and our grid size can be at most $50$. In our binary solution we used a $2 \times 2$ grid to multiply the number of ways by $2$. What about using other grid sizes instead?↵
↵
<spoiler summary="Full Solution">↵
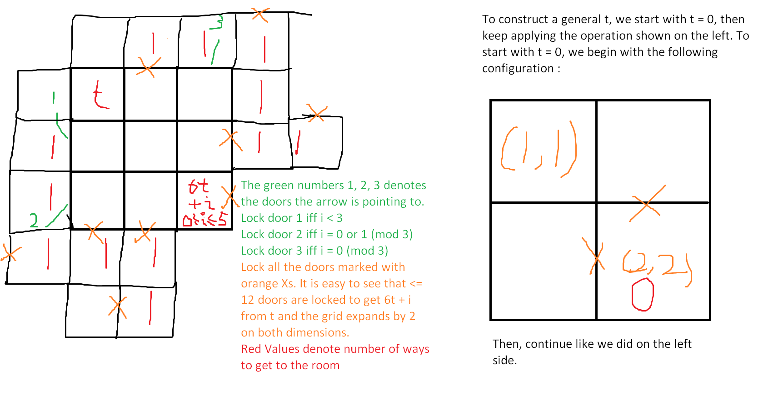
Our AC solution uses base $6$ instead of binary. Write $t$ in base $6$. Note that $t$ has at most $24$ digits in base $6$, so to add a new digit we can increase the dimensions by $2$ and the number of deleted edges can be up to $12$ per digit. We'll construct such a way. This method is explained in the picture below. The key is to first construct a grid which has $0$ in it, then find a way to get $6x + i$ for all $0 \le i \le 5$ from $x$ by maintaining a wall of $1$s around the squares. This method uses a $50 \times 50 (2 \cdot 24 + 2 = 50)$ grid and at most $24 \cdot 12 + 2 = 290$ edge deletions and will get AC.↵
↵
↵
</spoiler>↵
↵
Of course, this might not be the only way to solve this problem. Can you come up with other ways of solving this or reducing the constraints even further? (Open Question)↵
↵
Time Complexity : $O(\log t)$↵
↵
<spoiler summary="Code">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<int,int> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int INF = 1e9 + 7;↵
const int MOD = 1e9 + 7;↵
↵
typedef pair<ii,ii> move;↵
↵
set<move> ans;↵
int curx, cury;↵
↵
bool isvalid(move x)↵
{↵
if(x.fi.fi > 0 && x.se.fi > 0 && x.fi.se > 0 && x.se.se > 0 && x.fi.fi <= curx && x.fi.se <= cury && x.se.fi <= curx && x.se.se <= cury) return true;↵
return false;↵
}↵
↵
void edge(int x1, int y1, int x2, int y2)↵
{↵
ans.insert(mp(mp(x1, y1), mp(x2, y2)));↵
}↵
↵
void add(int bit)↵
{↵
int x = curx;↵
edge(x,x+2,x,x+3);↵
edge(x+1,x+2,x+1,x+3);↵
edge(x+2,x,x+3,x);↵
edge(x+2,x+1,x+3,x+1);↵
edge(x-2,x+3,x-1,x+3);↵
edge(x,x+4,x+1,x+4);↵
edge(x+3,x-2,x+3,x-1);↵
edge(x+4,x,x+4,x+1);↵
edge(x-1,x+1,x,x+1);↵
if(bit%3==0) edge(x-1,x+2,x,x+2);↵
if(bit%3!=2) edge(x+2,x-1,x+2,x);↵
if(bit<3) edge(x+1,x-1,x+1,x);↵
curx += 2; cury += 2;↵
}↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
ll t; cin >> t;↵
vector<int> digits;↵
while(t)↵
{↵
digits.pb(t%6);↵
t/=6;↵
}↵
reverse(digits.begin(), digits.end());↵
edge(1, 2, 2, 2);↵
edge(2, 1, 2, 2);↵
curx = 2; cury = 2;↵
for(int i = 0; i < digits.size(); i++)↵
{↵
add(digits[i]);↵
}↵
cout << curx << ' ' << cury << '\n';↵
vector<move> clr;↵
for(set<move>::iterator it = ans.begin(); it != ans.end(); it++)↵
{↵
if(!isvalid(*it))↵
{↵
clr.pb(*it);↵
}↵
}↵
for(int i = 0; i < clr.size(); i++)↵
{↵
ans.erase(clr[i]);↵
}↵
cout << ans.size() << '\n';↵
for(set<move>::iterator it = ans.begin(); it != ans.end(); it++)↵
{↵
move tmp = (*it);↵
cout << tmp.fi.fi << ' ' << tmp.fi.se << ' ' << tmp.se.fi << ' ' << tmp.se.se << '\n';↵
}↵
}↵
~~~~~↵
</spoiler>↵
↵
[Div. 1 E — Complete The Permutations](http://mirror.codeforces.com/contest/715/problem/E)↵
------------------↵
↵
Prerequisites : Math, Graph Theory, DP, Any fast multiplication algorithm↵
↵
We'll slowly unwind the problem and reduce it to something easier to count. First, we need to determine a way to tell when the distance between $p$ and $q$ is exactly $k$. This is a classic problem but I'll include it here for completeness.↵
↵
Let $f$ denote the inverse permutation of $q$. So, the minimum number of swaps to transform $p$ into $q$ is the minimum number of swaps to transform $p_{f_{i}}$ into the identity permutation. Construct the graph where the edges are $i \rightarrow p_{f_{i}}$ for all $1 \le i \le n$. Now, note that the graph is equivalent to $q_{i} \rightarrow p_{i}$ and is composed of disjoint cycles after $q_{i}$ and $p_{i}$ are filled completely. Note that the direction of the edges doesn't matter so we consider the edges to be $p_{i} \rightarrow q_{i}$ for all $1 \le i \le n$. Note that if the number of cycles of the graph is $t$, then the minimum number of swaps needed to transform $p$ into $q$ would be $n - t$. (Each swap can break one cycle into two) This means we just need to find the number of ways to fill in the empty spaces such that the number of cycles is exactly $i$ for all $1 \le i \le n$.↵
↵
Now, some of the values $p_{i}$ and $q_{i}$ are known. The edges can be classified into four types : ↵
↵
A-type : The edges of the form $x \rightarrow ?$, i.e. $p_{i}$ is known, $q_{i}$ isn't.↵
↵
B-type : The edges of the form $? \rightarrow x$, i.e. $q_{i}$ is known, $p_{i}$ isn't.↵
↵
C-type : The edges of the form $x \rightarrow y$, i.e. both $p_{i}$ and $q_{i}$ are known.↵
↵
D-type : The edges of the form $? \rightarrow ?$, i.e. both $p_{i}$ and $q_{i}$ are unknown.↵
↵
Now, the problem reduces to finding the number of ways to assign values to the question marks such that the number of cycles of the graph is exactly $i$ for all $1 \le i \le n$. First, we'll simplify the graph slightly. While there exists a number $x$ appears twice (clearly it can't appear more than twice) among the edges, we will combine the edges with $x$ together to simplify the graph. If there's an edge $x \rightarrow x$, then we increment the total number of cycles by $1$ and remove this edge from the graph. If there is an edge $a \rightarrow x$ and $x \rightarrow b$, where $a$ and $b$ might be some given numbers or question marks, then we can merge them together to form the edge $a \rightarrow b$. Clearly, these are the only cases for $x$ to appear twice. Hence, after doing all the reductions, we're reduced to edges where each known number appears at most once, i.e. all the known numbers are distinct. We'll do this step in $O(n^2)$. For each number $x$, store the position $i$ such that $p_{i} = x$ and also the position $j$ such that $q_{j} = x$, if it has already been given and $-1$ otherwise. So, we need to remove a number when the $i$ and $j$ stored are both positive. We iterate through the numbers from $1$ to $n$. If we need to remove a number, we go to the two positions where it occur and replace the two edges with the new merged one. Then, recompute the positions for all numbers (takes $O(n)$ time). So, for each number, we used $O(n)$ time. (to remove naively and update positions) Thus, the whole complexity for this part is $O(n^2)$. (It is possible to do it in $O(n)$ with a simple dfs as well. Basically almost any correct way of doing this part that is at most $O(n^3)$ works, since the constraints for $n$ is low)↵
↵
Now, suppose there are $m$ edges left and $p$ known numbers remain. Note that in the end when we form the graph we might join edges of the form $a \rightarrow ?$ and $? \rightarrow b$ (where $a$ and $b$ are either fixed numbers or question marks) together. So, the choice for the $?$ can be any of the $m - p$ remaining unused numbers. Note that there will be always $m - p$ such pairs so we need to multiply our answer by $(m - p)!$ in the end. Also, note that the $?$ are distinguishable, and order is important when filling in the blanks.↵
↵
So, we can actually reduce the problem to the following : Given integers $a, b, c, d$ denoting the number of A-type, B-type, C-type, D-type edges respectively. Find the number of ways to create $k$ cycles using them, for all $1 \le k \le n$. Note that the answer is only dependent on the values of $a, b, c, d$ as the numbers are all distinct after the reduction.↵
↵
First, we'll look at how to solve the problem for $k = 1$. We need to fit all the edges in a single cycle. First, we investigate what happens when $d = 0$. Note that we cannot have a B-type and C-type edge before an A-type or C-type edge, since all numbers are distinct so these edges can't be joined together. Similarly, an A or C-type edge cannot be directly after a B or C-type edge. Thus, with these restrictions, it is easy to see that the cycle must contain either all A-type edges or B-type edges. So, the answer can be easily calculated. It is also important to note that if we ignore the cyclic property then a contiguous string of edges without D must be of the form AA...BB.. or AA...CBB..., where there is only one C, and zero or more As and Bs.↵
↵
Now, if $d \ge 1$, we can fix one of the D-type edges as the front of the cycle. This helps a lot because now we can ignore the cyclic properties. (we can place anything at the end of the cycle because D-type edges can connect with any type of edges) So, we just need to find the number of ways to make a length $n - 1$ string with $a$ As, $b$ Bs, $c$ Cs and $d - 1$ Ds. In fact, we can ignore the fact that the A-type edges, B-type edges, C-type edges and D-type edges are distinguishable and after that multiply the answer by $a!b!c!(d-1)!$.↵
↵
We can easily find the number of valid strings we can make. First, place all the Ds. Now, we're trying to insert the As, Bs and Cs into the $d$ empty spaces between, after and before the Ds. The key is that by our observation above, we only care about how many As, Bs and Cs we insert in each space since after that the way to put that in is uniquely determined. So, to place the As and Bs, we can use the balls in urns formula to find that the number of ways to place the As is $\binom{a + d - 1}{d - 1}$ and the number of ways to place the Bs is $\binom{b + d - 1}{d - 1}$. The number of ways to place the Cs is $\binom{d}{c}$, since we choose where the Cs should go.↵
↵
Thus, it turns out that we can find the answer in $O(1)$ (with precomputing binomial coefficients and factorials) when $k = 1$. We'll use this to find the answer for all $k$. In the general case, there might be cycles that consists entirely of As and entirely of Bs, and those that contains at least one D. We call them the A-cycle, B-cycle and D-cycles respectively. ↵
↵
Now, we precompute $f(n, k)$, the number of ways to form $k$ cycles using $n$ distinguishable As. This can be done with a simple dp in $O(n^3)$. We iterate through the number of As we're using for the first cycle. Then, suppose we use $m$ As. The number of ways to choose which of the $m$ As to use is $\binom{n}{m}$ and we can permute them in $(m - 1)!$ ways inside the cycle. (not $m!$ because we have to account for all the cyclic permutations) Also, after summing this for all $m$, we have to divide the answer by $k$, to account for overcounting the candidates for the first cycle (the order of the $k$ cycles are not important)↵
↵
Thus, $f(n, k)$ can be computed in $O(n^3)$. First, we see how to compute the answer for a single $k$. Fix $x, y, e, f$, the number of A-cycles, B-cycles, number of As in total among the A-cycles and number of Bs in total among the B-cycles. Then, since $k$ is fixed, we know that the number of D-cycles is $k - x - y$. Now, we can find the answer in $O(1)$. First, we can use the values of $f(e, x), f(f, y), f(d, k - x - y)$ to determine the number of ways to place the Ds, and the As, Bs that are in the A-cycles and B-cycles. Then, to place the remaining As, Bs and Cs, we can use the same method as we did for $k = 1$ in $O(1)$, since the number of spaces to place them is still the same. (You can think of it as each D leaves an empty space to place As, Bs and Cs to the right of it) After that, we multiply the answer by $\binom{a}{e} \cdot \binom{b}{f}$ to account for the choice of the set of As and Bs used in the A-only and B-only cycles. Thus, the complexity of this method is $O(n^4)$ for each $k$ and $O(n^5)$ in total, which is clearly too slow.↵
↵
We can improve this by iterating through all $x + y, e, f$ instead. So, for this to work we need to precompute $f(e, 0)f(f, x + y) + f(e, 1)f(f, x + y - 1) + ... + f(e, x + y)f(f, 0)$, which we can write as $g(x + y, e, f)$. Naively doing this precomputation gives $O(n^4)$. Then, we can calculate the answer by iterating through all $x + y, e, f$ and thus getting $O(n^3)$ per query and $O(n^4)$ for all $k$. This is still too slow to pass $n = 250$.↵
↵
We should take a closer look of what we're actually calculating. Note that for a fixed pair $e, f$, the values of $g(x + y, e, f)$ can be calculated for all possible $x + y$ in $O(n\log n)$ or $O(n^{1.58})$ by using Number Theoretic Transform or Karatsuba's Algorithm respectively. (note that the modulus has been chosen for NFT to work) This is because if we fix $e, f$, then we're precisely finding the coefficients of the polynomial $(f(e, 0)x^{0} + f(e, 1)x^{1} + ... + f(e, n)x^{n})(f(f, 0)x^{0} + f(f, 1)x^{1} + ... + f(f, n)x^{n})$, so this can be handled with NFT/Karatsuba.↵
↵
Thus, the precomputation of $g(x + y, e, f)$ can be done in $O(n^3\log n)$ or $O(n^{3.58})$.↵
↵
Next, suppose we fixed $e$ and $f$. We will calculate the answer for all possible $k$ in $O(n\log n)$ similar to how we calculated $g(x + y, e, f)$. This time, we're multiplying the following two polynomials : $f(d, 0)x^{0} + f(d, 1)x^{1} + ... + f(d, n)x^{n}$ and $g(0, e, f)x^{0} + g(1, e, f)x^{1} + ... + g(n, e, f)x^{n}$. Again, we can calculate this using any fast multiplication method, so the entire solution takes $O(n^3\log n)$ or $O(n^{3.58})$, depending on which algorithm is used to multiply polynomials.↵
↵
Note that if you're using NFT/FFT, there is a small trick that can save some time. When we precompute the values of $g(x + y, e, f)$, we don't need to do inverse FFT on the result and leave it in the FFTed form. After that, when we want to find the convolution of $f(d, i)$ and $g(i, e, f)$, we just need to apply FFT to the first polynomial and multiply them. This reduces the number of FFTs and it reduced my solution runtime by half.↵
↵
Time Complexity : $O(n^3\log n)$ or $O(n^{3.58})$, depending on whether NFT or Karatsuba is used.↵
↵
<spoiler summary="Code (NFT)">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<int,int> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int N = 251;↵
const int MOD = 998244353;↵
ll inv2;↵
ll prt;↵
ll iprt;↵
↵
ll dpncr[N][N];↵
ll fact[N];↵
ll inverse[N];↵
ll g[N][N];↵
ll sumg[N][N][N];↵
↵
vector<ii> perm;↵
int A, B, C, D;↵
↵
ll modpow(ll a, ll b)↵
{↵
ll r = 1;↵
while(b)↵
{↵
if(b&1) r = (r*a)%MOD;↵
a = (a*a)%MOD;↵
b>>=1;↵
}↵
return r;↵
}↵
↵
ll inv(ll a)↵
{↵
return modpow(a, MOD - 2);↵
}↵
↵
ll choose(int n, int m)↵
{↵
if(m < 0) return 0;↵
if(n < m) return 0;↵
if(m == 0) return 1;↵
if(n == m) return 1;↵
if(dpncr[n][m] != -1) return dpncr[n][m];↵
dpncr[n][m] = choose(n - 1, m - 1) + choose(n - 1, m);↵
dpncr[n][m] += MOD; dpncr[n][m] %= MOD;↵
return dpncr[n][m];↵
}↵
↵
void computefact()↵
{↵
fact[0] = 1;↵
for(ll i = 1; i < N; i++)↵
{↵
fact[i] = (fact[i - 1]*i)%MOD;↵
}↵
for(ll i = 1; i < N; i++)↵
{↵
inverse[i] = modpow(i, MOD - 2);↵
}↵
}↵
↵
void print(vector<ii>& vec)↵
{↵
for(int i = 0; i < vec.size(); i++)↵
{↵
cout << vec[i].fi << ' ' << vec[i].se << endl;↵
}↵
cout << "------------------------------------------------" << endl;↵
}↵
↵
void printans(vector<ll>& vec)↵
{↵
for(int i = 0; i < vec.size(); i++)↵
{↵
cout << vec[i] << ' ';↵
}↵
cout << endl;↵
}↵
↵
void printansi(vector<int>& vec)↵
{↵
for(int i = 0; i < vec.size(); i++)↵
{↵
cout << vec[i] << ' ';↵
}↵
cout << endl;↵
}↵
↵
void calcpos(vector<ii>& pos)↵
{↵
pos.resize(perm.size());↵
for(int i = 0; i < perm.size(); i++)↵
{↵
pos[i] = ii(-1, -1);↵
}↵
for(int i = 1; i < perm.size(); i++)↵
{↵
if(perm[i].fi > 0)↵
{↵
pos[perm[i].fi].fi = i;↵
}↵
if(perm[i].se > 0)↵
{↵
pos[perm[i].se].se = i;↵
}↵
}↵
}↵
↵
int reduce()↵
{↵
int n = perm.size() - 1;↵
vector<ii> pos;↵
int cnt = 0;↵
for(int i = 1; i <= n; i++) //Do a reduction↵
{↵
calcpos(pos);↵
//print(pos);↵
if(pos[i].fi > 0 && pos[i].se > 0)↵
{↵
if(pos[i].fi == pos[i].se) ↵
{↵
cnt++;↵
ii tmp1 = perm[pos[i].fi];↵
for(vector<ii>::iterator it = perm.begin(); it != perm.end(); it++)↵
{↵
if((*it) == tmp1)↵
{↵
perm.erase(it); break;↵
}↵
}↵
continue;↵
}↵
int p1 = pos[i].se; int l = perm[p1].fi; ii tmp1 = perm[p1];↵
int p2 = pos[i].fi; int r = perm[p2].se; ii tmp2 = perm[p2];↵
for(vector<ii>::iterator it = perm.begin(); it != perm.end(); it++)↵
{↵
if((*it) == tmp1)↵
{↵
perm.erase(it); break;↵
}↵
}↵
for(vector<ii>::iterator it = perm.begin(); it != perm.end(); it++)↵
{↵
if((*it) == tmp2)↵
{↵
perm.erase(it); break;↵
}↵
}↵
perm.pb(ii(l, r));↵
}↵
}↵
//count A, B, C, D↵
for(int i = 1; i < perm.size(); i++)↵
{↵
if(perm[i].fi > 0 && perm[i].se > 0)↵
{↵
assert(perm[i].fi != perm[i].se);↵
C++;↵
}↵
else if(perm[i].fi > 0)↵
{↵
A++;↵
}↵
else if(perm[i].se > 0)↵
{↵
B++;↵
}↵
else↵
{↵
D++;↵
}↵
}↵
return cnt;↵
}↵
↵
ll mult(ll a, ll b)↵
{↵
ll r = (a*b)%MOD;↵
r = (r+MOD)%MOD;↵
return r;↵
}↵
↵
ll add(ll a, ll b)↵
{↵
ll r = ((a+b)%MOD+MOD)%MOD;↵
return r;↵
}↵
↵
ll F(ll a, ll b, ll c, ll d)↵
{↵
ll ans = 1;↵
if(d == 0)↵
{↵
if(a == 0 && b == 0 && c == 0) return 1;↵
else return 0;↵
}↵
ans = mult(ans, fact[a]);↵
ans = mult(ans, fact[b]);↵
ans = mult(ans, fact[c]);↵
ans = mult(ans, choose(a+d-1, d-1));↵
ans = mult(ans, choose(b+d-1, d-1));↵
ans = mult(ans, choose(d, C));↵
return ans;↵
}↵
↵
const int LG = 9;↵
const int root_pw = (1<<LG);↵
void fft (vector<int> & a, bool invert) ↵
{↵
int n = (int) a.size();↵
↵
for (int i=1, j=0; i<n; ++i) {↵
int bit = n >> 1;↵
for (; j>=bit; bit>>=1)↵
j -= bit;↵
j += bit;↵
if (i < j)↵
swap (a[i], a[j]);↵
}↵
↵
for (int len=2; len<=n; len<<=1) {↵
int wlen = invert ? iprt : prt;↵
for (int i=len; i<root_pw; i<<=1)↵
wlen = int((wlen*1LL*wlen)%MOD);↵
for (int i=0; i<n; i+=len) {↵
int w = 1;↵
for (int j=0; j<len/2; ++j) {↵
int u = a[i+j]; int v = int((a[i+j+len/2]*1LL*w)%MOD);↵
a[i+j] = u+v < MOD ? u+v : u+v-MOD;↵
a[i+j+len/2] = u-v >= 0 ? u-v : u-v+MOD;↵
w = int (w * 1LL * wlen % MOD);↵
}↵
}↵
}↵
if (invert) {↵
ll nrev = inv(n);↵
for (int i=0; i<n; ++i)↵
a[i] = int((a[i]*1LL*nrev)%MOD);↵
}↵
}↵
↵
void multiply(vector<int>& a, vector<int>& b, vector<int>& res)↵
{↵
vector<int> fa(a.begin(), a.end()), fb(b.begin(), b.end());↵
int n = 1;↵
while(n < max(a.size(), b.size())) n <<= 1;↵
fa.resize(n); fb.resize(n);↵
//cerr << "A : "; printansi(fa); cerr << "B : "; printansi(fb);↵
fft(fa, 0); fft(fb, 0);↵
//cerr << "INVERT ONCE : ";↵
//printans(fa); printans(fb);↵
//fft(fa, 1); fft(fb, 1); cerr << "INVERT BACK A: "; printans(fa); cerr << "INVERT BACK B: "; printans(fb);↵
res.resize(n);↵
for(int i = 0; i < n; i++) res[i] = int((fa[i]*1LL*fb[i])%MOD);↵
//printans(fa);↵
fft(res, 1);↵
//cerr << "CONVOLUTION : "; printansi(res);↵
↵
}↵
↵
void computeg(int n)↵
{↵
g[0][0] = 1;↵
g[1][1] = 1;↵
for(int i = 2; i <= n; i++)↵
{↵
for(int j = 1; j <= i; j++)↵
{↵
for(int k = 1; k <= i; k++)↵
{↵
g[i][j] = add(g[i][j], mult(g[i-k][j-1], mult(choose(i, k), fact[k-1])));↵
}↵
//cerr << g[i][j] << '\n';↵
g[i][j] = mult(g[i][j], inverse[j]);↵
//cerr << "G : " << i << ' ' << j << ' ' << g[i][j] << '\n';↵
}↵
}↵
for(int i = 0; i <= A; i++)↵
{↵
for(int j = 0; j <= B; j++)↵
{↵
vector<int> gi; vector<int> gj;↵
gi.resize(n+1); gj.resize(n+1);↵
for(int k = 0; k <= n; k++)↵
{↵
gi[k] = int(g[i][k]);↵
gj[k] = int(g[j][k]);↵
//cerr << gi[k] << ' ' << gj[k] << '\n';↵
}↵
vector<int> res;↵
multiply(gi, gj, res);↵
for(int k = 0; k <= n; k++)↵
{↵
sumg[i][j][k] = res[k];↵
}↵
}↵
}↵
}↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
int n; cin >> n; perm.resize(n+1);↵
for(int i = 1; i <= n; i++)↵
{↵
cin >> perm[i].fi;↵
}↵
for(int i = 1; i <= n; i++)↵
{↵
cin >> perm[i].se;↵
}↵
ll tmpmult = 7*17;↵
tmpmult = mult(tmpmult, modpow(2, 23 - LG)); ↵
prt = modpow(3, tmpmult);↵
inv2 = inv(2);↵
iprt = inv(prt);↵
A = 0; B = 0; C = 0; D = 0;↵
memset(dpncr, -1, sizeof(dpncr));↵
memset(sumg, 0, sizeof(sumg));↵
memset(g, 0, sizeof(g));↵
memset(fact, 0, sizeof(fact));↵
memset(inverse, 0, sizeof(inverse));↵
int cycles = reduce();↵
computefact(); ↵
computeg(n);↵
//cerr << h(1, 0, 0) << endl;↵
↵
vector<ll> ans; ans.assign(n+1, 0);↵
↵
if(D - C < 0)↵
{↵
for(int i = 0; i < n; i++)↵
{↵
cout << ans[i] << ' ';↵
}↵
cout << endl;↵
return 0;↵
}↵
↵
for(int i = 0; i <= A; i++)↵
{↵
for(int j = 0; j <= B; j++)↵
{↵
ll coef = 1;↵
coef = mult(coef, F(A-i,B-j,C,D));↵
if(A > 0) coef = mult(coef, choose(A, i));↵
if(B > 0) coef = mult(coef, choose(B, j));↵
vector<int> gi; vector<int> gj;↵
gi.resize(n+1); gj.resize(n+1);↵
for(int k = 0; k <= n - cycles; k++)↵
{↵
gi[k] = int(g[D][k]);↵
gj[k] = int(sumg[i][j][k]);↵
}↵
vector<int> res;↵
multiply(gi, gj, res);↵
//cout << gi.size() << ' ' << gj.size() << ' ' << res.size() << ' ' << ans.size() << ' ' << n << ' ' << cycles << '\n';↵
for(int k = 0; k <= n - cycles; k++)↵
{↵
int moves = n - (k + cycles);↵
ans[moves] = add(ans[moves], mult(res[k], coef));↵
}↵
}↵
}↵
↵
for(int i = 0; i < ans.size(); i++)↵
{↵
ans[i] = mult(ans[i], fact[D-C]);↵
}↵
↵
for(int i = 0; i < n; i++)↵
{↵
cout << ans[i] << ' ';↵
}↵
cout << endl;↵
↵
return 0;↵
}↵
~~~~~↵
</spoiler>↵
↵
<spoiler summary="Code (Karatsuba)">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<int,int> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int N = 251;↵
const int MOD = 998244353;↵
ll inv2;↵
ll prt;↵
ll iprt;↵
↵
ll dpncr[N][N];↵
ll fact[N];↵
ll inverse[N];↵
ll g[N][N];↵
ll sumg[N][N][N];↵
↵
vector<ii> perm;↵
int A, B, C, D;↵
↵
ll modpow(ll a, ll b)↵
{↵
ll r = 1;↵
while(b)↵
{↵
if(b&1) r = (r*a)%MOD;↵
a = (a*a)%MOD;↵
b>>=1;↵
}↵
return r;↵
}↵
↵
ll inv(ll a)↵
{↵
return modpow(a, MOD - 2);↵
}↵
↵
ll choose(int n, int m)↵
{↵
if(m < 0) return 0;↵
if(n < m) return 0;↵
if(m == 0) return 1;↵
if(n == m) return 1;↵
if(dpncr[n][m] != -1) return dpncr[n][m];↵
dpncr[n][m] = choose(n - 1, m - 1) + choose(n - 1, m);↵
dpncr[n][m] += MOD; dpncr[n][m] %= MOD;↵
return dpncr[n][m];↵
}↵
↵
void computefact()↵
{↵
fact[0] = 1;↵
for(ll i = 1; i < N; i++)↵
{↵
fact[i] = (fact[i - 1]*i)%MOD;↵
}↵
for(ll i = 1; i < N; i++)↵
{↵
inverse[i] = modpow(i, MOD - 2);↵
}↵
}↵
↵
void print(vector<ii>& vec)↵
{↵
for(int i = 0; i < vec.size(); i++)↵
{↵
cout << vec[i].fi << ' ' << vec[i].se << endl;↵
}↵
cout << "------------------------------------------------" << endl;↵
}↵
↵
void printans(vector<ll>& vec)↵
{↵
for(int i = 0; i < vec.size(); i++)↵
{↵
cout << vec[i] << ' ';↵
}↵
cout << endl;↵
}↵
↵
void printansi(vector<int>& vec)↵
{↵
for(int i = 0; i < vec.size(); i++)↵
{↵
cout << vec[i] << ' ';↵
}↵
cout << endl;↵
}↵
↵
void calcpos(vector<ii>& pos)↵
{↵
pos.resize(perm.size());↵
for(int i = 0; i < perm.size(); i++)↵
{↵
pos[i] = ii(-1, -1);↵
}↵
for(int i = 1; i < perm.size(); i++)↵
{↵
if(perm[i].fi > 0)↵
{↵
pos[perm[i].fi].fi = i;↵
}↵
if(perm[i].se > 0)↵
{↵
pos[perm[i].se].se = i;↵
}↵
}↵
}↵
↵
int reduce()↵
{↵
int n = perm.size() - 1;↵
vector<ii> pos;↵
int cnt = 0;↵
for(int i = 1; i <= n; i++) //Do a reduction↵
{↵
calcpos(pos);↵
//print(pos);↵
if(pos[i].fi > 0 && pos[i].se > 0)↵
{↵
if(pos[i].fi == pos[i].se) ↵
{↵
cnt++;↵
ii tmp1 = perm[pos[i].fi];↵
for(vector<ii>::iterator it = perm.begin(); it != perm.end(); it++)↵
{↵
if((*it) == tmp1)↵
{↵
perm.erase(it); break;↵
}↵
}↵
continue;↵
}↵
int p1 = pos[i].se; int l = perm[p1].fi; ii tmp1 = perm[p1];↵
int p2 = pos[i].fi; int r = perm[p2].se; ii tmp2 = perm[p2];↵
for(vector<ii>::iterator it = perm.begin(); it != perm.end(); it++)↵
{↵
if((*it) == tmp1)↵
{↵
perm.erase(it); break;↵
}↵
}↵
for(vector<ii>::iterator it = perm.begin(); it != perm.end(); it++)↵
{↵
if((*it) == tmp2)↵
{↵
perm.erase(it); break;↵
}↵
}↵
perm.pb(ii(l, r));↵
}↵
}↵
//count A, B, C, D↵
for(int i = 1; i < perm.size(); i++)↵
{↵
if(perm[i].fi > 0 && perm[i].se > 0)↵
{↵
assert(perm[i].fi != perm[i].se);↵
C++;↵
}↵
else if(perm[i].fi > 0)↵
{↵
A++;↵
}↵
else if(perm[i].se > 0)↵
{↵
B++;↵
}↵
else↵
{↵
D++;↵
}↵
}↵
return cnt;↵
}↵
↵
ll mult(ll a, ll b)↵
{↵
ll r = (a*b)%MOD;↵
r = (r+MOD)%MOD;↵
return r;↵
}↵
↵
ll add(ll a, ll b)↵
{↵
ll r = ((a+b)%MOD+MOD)%MOD;↵
return r;↵
}↵
↵
ll F(ll a, ll b, ll c, ll d)↵
{↵
ll ans = 1;↵
if(d == 0)↵
{↵
if(a == 0 && b == 0 && c == 0) return 1;↵
else return 0;↵
}↵
ans = mult(ans, fact[a]);↵
ans = mult(ans, fact[b]);↵
ans = mult(ans, fact[c]);↵
ans = mult(ans, choose(a+d-1, d-1));↵
ans = mult(ans, choose(b+d-1, d-1));↵
ans = mult(ans, choose(d, C));↵
return ans;↵
}↵
↵
ll buffer[20001], bufferpos, siz = 1024;↵
const int LG = 4;↵
↵
void multiply(int size, ll a[], ll b[], ll r[])↵
{↵
if(size <= (1<<LG))↵
{↵
for(int i = 0; i < size*2; i++) r[i] = 0;↵
for(int i = 0; i < size; i++)↵
{↵
if(a[i])↵
{↵
for(int j = 0; j < size; j++)↵
{↵
r[i+j] += a[i]*b[j];↵
r[i+j] %= MOD;↵
}↵
}↵
}↵
for(int i = 0; i < size*2; i++)↵
{↵
r[i] %= MOD;↵
}↵
return ;↵
}↵
int s = size/2;↵
multiply(s, a, b, r);↵
multiply(s, a+s, b+s, r+size);↵
ll *a2 = buffer+bufferpos; bufferpos += s;↵
ll *b2 = buffer+bufferpos; bufferpos += s;↵
ll *r2 = buffer+bufferpos; bufferpos += size;↵
for(int i = 0; i < s; i++)↵
{↵
a2[i] = a[i] + a[i+s];↵
if(a2[i]>=MOD) a2[i]-=MOD;↵
}↵
for(int i = 0; i < s; i++)↵
{↵
b2[i] = b[i] + b[i+s];↵
if(b2[i]>=MOD) b2[i]-=MOD;↵
}↵
multiply(s, a2, b2, r2);↵
for(int i = 0; i < size; i++)↵
{↵
r2[i] -= (r[i] + r[i+size]);↵
}↵
for(int i = 0; i < size; i++)↵
{↵
r[i+s] += r2[i];↵
r[i+s]%=MOD;↵
if(r[i+s]<0) r[i+s]+=MOD;↵
}↵
bufferpos -= (s+s+size);↵
}↵
ll gi[N+5]; ll gj[N+5];↵
↵
void computeg(int n)↵
{↵
g[0][0] = 1;↵
g[1][1] = 1;↵
for(int i = 2; i <= n; i++)↵
{↵
for(int j = 1; j <= i; j++)↵
{↵
for(int k = 1; k <= i; k++)↵
{↵
g[i][j] = add(g[i][j], mult(g[i-k][j-1], mult(choose(i, k), fact[k-1])));↵
}↵
g[i][j] = mult(g[i][j], inverse[j]);↵
}↵
}↵
for(int i = 0; i <= A; i++)↵
{↵
for(int j = 0; j <= B; j++)↵
{↵
siz = 512;↵
while(siz/2 >= n+1) siz>>=1;↵
for(int k = 0; k < siz; k++)↵
{↵
if(k <= n)↵
{↵
gi[k] = g[i][k];↵
gj[k] = g[j][k];↵
}↵
else↵
{↵
gi[k] = gj[k] = 0;↵
}↵
}↵
ll *res = buffer+bufferpos;↵
bufferpos+=2*siz;↵
multiply(siz,gi,gj,res);↵
for(int k = 0; k <= n; k++)↵
{↵
sumg[i][j][k] = res[k];↵
}↵
bufferpos-=2*siz;↵
}↵
}↵
}↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
int n; cin >> n; perm.resize(n+1);↵
↵
for(int i = 1; i <= n; i++)↵
{↵
cin >> perm[i].fi;↵
}↵
for(int i = 1; i <= n; i++)↵
{↵
cin >> perm[i].se;↵
}↵
↵
A = 0; B = 0; C = 0; D = 0;↵
memset(dpncr, -1, sizeof(dpncr));↵
memset(sumg, 0, sizeof(sumg));↵
memset(g, 0, sizeof(g));↵
memset(fact, 0, sizeof(fact));↵
memset(inverse, 0, sizeof(inverse));↵
int cycles = reduce();↵
computefact(); computeg(n);↵
vector<ll> ans; ans.assign(n+1, 0);↵
↵
if(D - C < 0)↵
{↵
for(int i = 0; i < n; i++)↵
{↵
cout << ans[i] << ' ';↵
}↵
cout << endl;↵
return 0;↵
}↵
↵
for(int i = 0; i <= A; i++)↵
{↵
for(int j = 0; j <= B; j++)↵
{↵
ll coef = 1;↵
coef = mult(coef, F(A-i,B-j,C,D));↵
if(A > 0) coef = mult(coef, choose(A, i));↵
if(B > 0) coef = mult(coef, choose(B, j));↵
siz = 512;↵
while(siz/2 >= n-cycles+1) siz>>=1;↵
for(int k = 0; k < siz; k++)↵
{↵
if(k <= n-cycles)↵
{↵
gi[k] = g[D][k];↵
gj[k] = sumg[i][j][k];↵
}↵
else↵
{↵
gi[k] = gj[k] = 0;↵
}↵
}↵
ll *res = buffer+bufferpos;↵
bufferpos+=2*siz;↵
multiply(siz,gi,gj,res);↵
for(int k = 0; k <= n - cycles; k++)↵
{↵
int moves = n - (k + cycles);↵
ans[moves] = add(ans[moves], mult(res[k], coef));↵
}↵
bufferpos-=2*siz;↵
}↵
}↵
↵
for(int i = 0; i < ans.size(); i++)↵
{↵
ans[i] = mult(ans[i], fact[D-C]);↵
}↵
↵
for(int i = 0; i < n; i++)↵
{↵
cout << ans[i] << ' ';↵
}↵
cout << endl;↵
}↵
~~~~~↵
</spoiler>↵
↵
↵
[Div. 2 A — Crazy Computer](http://mirror.codeforces.com/contest/716/problem/A)↵
------------------↵
↵
Prerequisites : None↵
↵
This is a straightforward implementation problem. Iterate through the times in order, keeping track of when is the last time a word is typed, keeping a counter for the number of words appearing on the screen. Increment the counter by $1$ whenever you process a new time. Whenever the difference between the time for two consecutive words is greater than $c$, reset the counter to $0$. After that, increment it by $1$. ↵
↵
Time Complexity : $O(n)$, since the times are already sorted.↵
↵
<spoiler summary="Code (O(n))">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<int,int> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int N = 1e5 + 3;↵
ll a[N];↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
int n, c; cin >> n >> c;↵
for(int i = 0; i < n; i++)↵
{↵
cin >> a[i];↵
}↵
//sort(a, a + n);↵
int cnt = 0;↵
for(int i = 0; i < n; i++)↵
{↵
if(i == 0) cnt++;↵
else↵
{↵
if(a[i] - a[i - 1] <= c) cnt++;↵
else cnt = 1;↵
}↵
}↵
cout << cnt;↵
return 0;↵
}↵
~~~~~↵
</spoiler>↵
↵
[Div. 2 B — Complete The Word](http://mirror.codeforces.com/contest/716/problem/B)↵
------------------↵
↵
Prerequisites : None↵
↵
Firstly, if the length of the string is less than $26$, output $-1$ immediately.↵
↵
We want to make a substring of length $26$ have all the letters of the alphabet. Thus, the simplest way is to iterate through all substrings of length $26$ (there are $O(n)$ such substrings), then for each substring count the number of occurrences of each alphabet, ignoring the question marks. After that, if there exist a letter that occurs twice or more, this substring cannot contain all letters of the alphabet, and we process the next substring. Otherwise, we can fill in the question marks with the letters that have not appeared in the substring and obtain a substring of length $26$ which contains all letters of the alphabet. After iterating through all substrings, either there is no solution, or we already created a nice substring. If the former case appears, output $-1$. Otherwise, fill in the remaining question marks with random letters and output the string.↵
↵
Note that one can optimize the solution above by noting that we don't need to iterate through all $26$ letters of each substring we consider, but we can iterate through the substrings from left to right and when we move to the next substring, remove the front letter of the current substring and add the last letter of the next substring. This optimization is not required to pass.↵
↵
We can still optimize it further and make the complexity purely $O(|s|)$. We use the same trick as above, when we move to the next substring, we remove the previous letter and add the new letter. We store a frequency array counting how many times each letter appear in the current substring. Additionally, store a counter which we will use to detect whether the current substring can contain all the letters of the alphabet in $O(1)$. When a letter first appear in the frequency array, increment the counter by $1$. If a letter disappears (is removed) in the frequency array, decrement the counter by $1$. When we add a new question mark, increment the counter by $1$. When we remove a question mark, decrement the counter by $1$. To check whether a substring can work, we just have to check whether the counter is equal to $26$. This solution works in $O(|s|)$.↵
↵
Time Complexity : $O(|s| \cdot 26^{2})$, $O(|s| \cdot 26)$ or $O(|s|)$↵
↵
<spoiler summary="Code (O(26^2*|s|)">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<int,int> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int N = 10000;↵
int cnt[27];↵
string s; int n;↵
↵
bool valid()↵
{↵
for(int i = 0; i < 26; i++)↵
{↵
if(cnt[i] >= 2) return false;↵
}↵
return true;↵
}↵
↵
void fillall()↵
{↵
for(int i = 0; i < n; i++)↵
{↵
if(s[i] == '?') s[i] = 'A';↵
}↵
}↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
cin >> s;↵
n = s.length();↵
if(n < 26) {cout << -1; return 0;}↵
for(int i = 25; i < n; i++)↵
{↵
memset(cnt, 0, sizeof(cnt));↵
for(int j = i; j >= i - 25; j--)↵
{↵
cnt[s[j]-'A']++;↵
}↵
if(valid())↵
{↵
//cout << "GG " << i << '\n';↵
int cur = 0;↵
while(cnt[cur]>0) cur++;↵
for(int j = i - 25; j <= i; j++)↵
{↵
if(s[j] == '?')↵
{↵
s[j] = cur + 'A';↵
cur++;↵
while(cnt[cur]>0) cur++;↵
}↵
}↵
fillall();↵
cout << s;↵
return 0;↵
}↵
}↵
cout << -1;↵
return 0;↵
}↵
~~~~~↵
</spoiler>↵
↵
<spoiler summary="Code (O(26*|s|)">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<int,int> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int N = 10000;↵
int cnt[27];↵
string s; int n;↵
↵
bool valid()↵
{↵
for(int i = 0; i < 26; i++)↵
{↵
if(cnt[i] >= 2) return false;↵
}↵
return true;↵
}↵
↵
void fillall()↵
{↵
for(int i = 0; i < n; i++)↵
{↵
if(s[i] == '?') s[i] = 'A';↵
}↵
}↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
cin >> s;↵
n = s.length();↵
if(n < 26) {cout << -1; return 0;}↵
for(int i = 0; i < 26; i++) cnt[s[i]-'A']++;↵
if(valid())↵
{↵
int cur = 0;↵
while(cnt[cur]>0) cur++;↵
for(int i = 0; i < 26; i++)↵
{↵
if(s[i] == '?')↵
{↵
s[i] = cur + 'A';↵
cur++;↵
while(cnt[cur]>0) cur++;↵
}↵
}↵
fillall();↵
cout << s;↵
return 0;↵
}↵
for(int i = 26; i < n; i++)↵
{↵
cnt[s[i]-'A']++; cnt[s[i-26]-'A']--;↵
if(valid())↵
{↵
//cout << "GG " << i << '\n';↵
int cur = 0;↵
while(cnt[cur]>0) cur++;↵
for(int j = i - 25; j <= i; j++)↵
{↵
if(s[j] == '?')↵
{↵
s[j] = cur + 'A';↵
cur++;↵
while(cnt[cur]>0) cur++;↵
}↵
}↵
fillall();↵
cout << s;↵
return 0;↵
}↵
}↵
cout << -1;↵
return 0;↵
}↵
~~~~~↵
</spoiler>↵
↵
<spoiler summary="Code (O(|s|)">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<int,int> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int N = 50000;↵
int cnt[27];↵
string s; int n;↵
int counter;↵
↵
bool valid()↵
{↵
//cout << counter << endl;↵
return (counter == 26);↵
}↵
↵
void fillall()↵
{↵
for(int i = 0; i < n; i++)↵
{↵
if(s[i] == '?') s[i] = 'A';↵
}↵
}↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
cin >> s;↵
n = s.length();↵
if(n < 26) {cout << -1; return 0;}↵
counter = 0;↵
for(int i = 0; i < 26; i++)↵
{↵
if(s[i] == '?')↵
{↵
counter++; continue;↵
}↵
cnt[s[i]-'A']++;↵
if(cnt[s[i]-'A'] == 1) counter++;↵
}↵
if(valid())↵
{↵
int cur = 0;↵
while(cnt[cur]>0) cur++;↵
for(int i = 0; i < 26; i++)↵
{↵
if(s[i] == '?')↵
{↵
s[i] = cur + 'A';↵
cur++;↵
while(cnt[cur]>0) cur++;↵
}↵
}↵
fillall();↵
cout << s;↵
return 0;↵
}↵
for(int i = 26; i < n; i++)↵
{↵
if(s[i] != '?') {cnt[s[i]-'A']++; if(cnt[s[i]-'A']==1) counter++;}↵
if(s[i-26] != '?') {cnt[s[i-26]-'A']--; if(cnt[s[i-26]-'A']==0) counter--;}↵
if(s[i-26] == '?') counter--;↵
if(s[i] == '?') counter++;↵
if(valid())↵
{↵
int cur = 0;↵
while(cnt[cur]>0) cur++;↵
for(int j = i - 25; j <= i; j++)↵
{↵
if(s[j] == '?')↵
{↵
s[j] = cur + 'A';↵
cur++;↵
while(cnt[cur]>0) cur++;↵
}↵
}↵
fillall();↵
cout << s;↵
return 0;↵
}↵
}↵
cout << -1;↵
return 0;↵
}↵
~~~~~↵
</spoiler>↵
↵
[Div. 2 C/Div. 1 A — Plus and Square Root](http://mirror.codeforces.com/contest/715/problem/A)↵
------------------↵
↵
Prerequisites : None↵
↵
Firstly, let $a_{i} (1 \le i \le n)$ be the number on the screen before we level up from level $i$ to $i + 1$. Thus, we require all the $a_{i}$s to be perfect square and additionally to reach the next $a_{i}$ via pressing the plus button, we require $a_{i + 1} \equiv \sqrt{a_{i}} (mod (i + 1))$ and $a_{i + 1} \ge \sqrt{a_{i}}$ for all $1 \le i < n$. Additionally, we also require $a_{i}$ to be a multiple of $i$. Thus, we just need to construct a sequence of such integers so that the output numbers does not exceed the limit $10^{18}$. ↵
↵
There are many ways to do this. The third sample actually gave a large hint on my approach. If you were to find the values of $a_{i}$ from the second sample, you'll realize that it is equal to $4, 36, 144, 400$. You can try to find the pattern from here. My approach is to use $a_{i} = [i(i + 1)]^{2}$. Clearly, it is a perfect square for all $1 \le i \le n$ and when $n = 100000$, the output values can be checked to be less than $10^{18}$$. Additionally, we also have $a_{i + 1} = [(i + 1)(i + 2)]^
↵
The constraints $a_{i}$ must be a multiple of $i$ was added to make the problem easier for Div. 1 A.↵
↵
Time Complexity : $O(n)$↵
↵
<spoiler summary="Code (O(n))">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<ll,ll> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
ll n; cin >> n;↵
for(ll i = 1; i <= n; i++)↵
{↵
if(i == 1) cout << 2 << '\n';↵
else cout << i*(i+1)*(i+1)-(i-1) << '\n';↵
}↵
return 0;↵
}↵
↵
~~~~~↵
</spoiler>↵
↵
[Div. 2 D/Div. 1 B — Complete The Graph](http://mirror.codeforces.com/contest/715/problem/B)↵
------------------↵
↵
Prerequisites : Dijkstra's Algorithm↵
↵
This problem is actually quite simple if you rule out the impossible conditions. Call the edges that does not have fixed weight variable edges. First, we'll determine when a solution exists.↵
↵
Firstly, we ignore the variable edges. Now, find the length of the shortest path from $s$ to $e$. If this length is $< L$, there is no solution, since even if we replace the $0$ weights with any positive weight the shortest path will never exceed this shortest path. Thus, if the length of this shortest path is $< L$, there is no solution. (If no path exists we treat the length as $\infty$.)↵
↵
Next, we replace the edges with $0$ weight with weight $1$. Clearly, among all the possible graphs you can generate by replacing the weights, this graph will give the minimum possible shortest path from $s$ to $e$, since increasing any weight will not decrease the length of the shortest path. Thus, if the shortest path of this graph is $> L$, there is no solution, since the shortest path will always be $> L$. If no path exists we treat the length as $\infty$.↵
↵
Other than these two conditions, there will always be a way to assign the weights so that the shortest path from $s$ to $e$ is exactly $L$! How do we prove this? First, consider all paths from $s$ to $e$ that has at least one $0$ weight edge, as changing weights won't affect the other paths. Now, we repeat this algorithm. Initially, assign all the weights as $1$. Then, sort the paths in increasing order of length. If the length of the shortest path is equal to $L$, we're done. Otherwise, increase the weight of one of the variable edges on the shortest path by $1$. Note that this will increase the lengths of some of the paths by $1$. It is not hard to see that by repeating these operations the shortest path will eventually have length $L$, so an assignment indeed exists.↵
↵
Now, we still have to find a valid assignment of weights. We can use a similar algorithm as our proof above. Assign $1$ to all variable edges first. Next, we first find and keep track of the shortest path from $s$ to $e$. Note that if this path has no variable edges it must have length exactly $L$ or strictly more than $L$, so either we're already done or the shortest path contains variable edges and the length is strictly less than $L$. (otherwise we're done)↵
↵
From now on, whenever we assign weight to a variable edge (after assigning $1$ to every variable edge), we call the edge assigned.↵
↵
Now, mark all variable edges not on the shortest path we found as $\infty$ weight. (we can choose any number greater than $L$ as $\infty$) Next, we will find the shortest path from $s$ to $e$, and replace the weight of an unassigned variable edge such that the length of the path becomes equal to $L$. Now, we don't touch the assigned edges again. While the shortest path from $s$ to $e$ is still strictly less than $L$, we repeat the process and replace a variable edge that is not assigned such that the path length is equal to $L$. Note that this is always possible, since otherwise this would've been the shortest path in one of the previous steps. Eventually, the shortest path from $s$ to $e$ will have length exactly $L$. It is easy to see that we can repeat this process at most $n$ times because we are only replacing the edges which are on the initial shortest path we found and there are less than $n$ edges to replace (we only touch each edge at most once). Thus, we can find a solution after less than $n$ iterations. So, the complexity becomes $O(mn \log n)$. This is sufficient to pass all tests.↵
↵
What if the constraints were $n, m \le 10^{5}$? Can we do better? ↵
↵
Yes! Thanks to [user:HellKitsune,2016-09-17] who found this solution during testing. First, we rule out the impossible conditions like we did above. Then, we assign all the variable edges with $\infty$ weight. We enumerate the variable edges arbitarily. Now, we binary search to find the minimal value $p$ such that if we make all the variable edges numbered from $1$ to $p$ have weight $1$ and the rest $\infty$, then the shortest path from $s$ to $e$ has length $\le L$. Now, note that if we change the weight of $p$ to $\infty$ the length of shortest path will be more than $L$. (if $p$ equals the number of variable edges, the length of the shortest path is still more than $L$ or it will contradict the impossible conditions) If the weight is $1$, the length of the shortest path is $\le L$. So, if we increase the weight of edge $p$ by $1$ repeatedly, the length of the shortest path from $s$ to $e$ will eventually reach $L$, since this length can increase by at most $1$ in each move. So, since the length of shortest path is non-decreasing when we increase the weight of this edge, we can binary search for the correct weight. This gives an $O(m\log n (\log m + \log L))$ solution.↵
↵
Time Complexity : $O(mn\log n)$ or $O(m\log n (\log m + \log L))$↵
↵
<spoiler summary="Code (O(mnlogn))">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<ll,ll> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int N = 1001;↵
const int M = 10001;↵
const ll INF = ll(1e18);↵
↵
vector<ii> adj[N];↵
vector<int> adj2[N];↵
int L[M]; int R[M];↵
ll d1[N];↵
ll d2[N];↵
int par[N];↵
ll dist[N][N];↵
↵
int n, m, l, s, e;↵
↵
void dijkstra()↵
{↵
d1[s] = 0;↵
priority_queue<ii, vector<ii>, greater<ii> > pq;↵
pq.push(ii(0, s));↵
int cnt = 0;↵
while(!pq.empty())↵
{↵
cnt++;↵
int u = pq.top().se; ll d = pq.top().fi; pq.pop();↵
for(int i = 0; i < adj[u].size(); i++)↵
{↵
int v = adj[u][i].fi; ll w = adj[u][i].se;↵
if(d + w < d1[v])↵
{↵
d1[v] = d + w;↵
pq.push(ii(d1[v], v));↵
}↵
}↵
}↵
cerr << "DIJKSTRA OPERATIONS : " << cnt << '\n';↵
}↵
↵
bool dijkstra2()↵
{↵
d2[s] = 0;↵
priority_queue<ii, vector<ii>, greater<ii> > pq;↵
pq.push(ii(0, s));↵
while(!pq.empty())↵
{↵
int u = pq.top().se; ll d = pq.top().fi; pq.pop();↵
for(int i = 0; i < adj2[u].size(); i++)↵
{↵
int v = adj2[u][i]; ll w = dist[u][v];↵
if(d + abs(w) < d2[v])↵
{↵
d2[v] = d + abs(w);↵
par[v] = u;↵
pq.push(ii(d2[v], v));↵
}↵
}↵
}↵
if(d2[e] > l) return false;↵
int cur = e;↵
while(cur != s)↵
{↵
int p = par[cur];↵
if(dist[p][cur] < 0)↵
{↵
dist[p][cur] = -2; dist[cur][p] = -2;↵
}↵
cur = par[cur];↵
}↵
for(int i = 0; i < n; i++)↵
{↵
for(int j = 0; j < n; j++)↵
{↵
if(dist[i][j] == -1)↵
{↵
dist[i][j] = INF;↵
}↵
}↵
}↵
cur = e;↵
while(cur != s)↵
{↵
int p = par[cur];↵
if(dist[p][cur] < 0)↵
{↵
dist[p][cur] = -1; dist[cur][p] = -1;↵
}↵
cur = par[cur];↵
}↵
return true;↵
}↵
↵
void print()↵
{↵
cout << "YES\n";↵
for(int i = 0; i < m; i++)↵
{↵
int u = L[i]; int v = R[i];↵
ll d = dist[u][v];↵
if(d < 0) d = -d;↵
cout << u << ' ' << v << ' ' << d << '\n';↵
}↵
}↵
↵
bool relax()↵
{↵
for(int i = 0; i < n; i++) d2[i] = INF;↵
memset(par, -1, sizeof(par)); //shouldn't be neccesary↵
d2[s] = 0;↵
priority_queue<ii, vector<ii>, greater<ii> > pq;↵
pq.push(ii(0, s));↵
while(!pq.empty())↵
{↵
int u = pq.top().se; ll d = pq.top().fi; pq.pop();↵
for(int i = 0; i < adj2[u].size(); i++)↵
{↵
int v = adj2[u][i]; ll w = dist[u][v];↵
if(d + abs(w) < d2[v])↵
{↵
d2[v] = d + abs(w);↵
par[v] = u;↵
pq.push(ii(d2[v], v));↵
}↵
}↵
}↵
//cerr << d2[e] << '\n';↵
if(d2[e] == l) return true;↵
int cur = e; bool meet = false;↵
while(cur != s)↵
{↵
int p = par[cur];↵
if(!meet && dist[p][cur] < 0)↵
{↵
ll d = abs(dist[p][cur]);↵
dist[p][cur] = d + l - d2[e];↵
dist[cur][p] = d + l - d2[e];↵
//cerr << d << endl;↵
meet = true;↵
}↵
if(meet) break;↵
cur = par[cur];↵
}↵
return false;↵
}↵
↵
int dist1[N][N];↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
cin >> n >> m >> l >> s >> e;↵
memset(dist1, -1, sizeof(dist1));↵
for(int i = 0; i < m; i++)↵
{↵
int u, v, w; cin >> u >> v >> w;↵
if(w > 0) ↵
{↵
adj[u].pb(ii(v, w)); adj[v].pb(ii(u, w));↵
adj2[u].pb(v); adj2[v].pb(u);↵
dist1[u][v] = w; dist1[v][u] = w;↵
dist[u][v] = w; dist[v][u] = w;↵
}↵
else↵
{↵
adj2[u].pb(v); adj2[v].pb(u);↵
dist[u][v] = -1; dist[v][u] = -1;↵
}↵
L[i] = u; R[i] = v;↵
} ↵
for(int i = 0; i < n; i++)↵
{↵
d1[i] = INF; d2[i] = INF;↵
}↵
dijkstra(); //cerr << d1[e] << '\n';↵
if(d1[e] < l)↵
{↵
cout << "NO\n";↵
return 0;↵
}↵
if(d1[e] == l)↵
{↵
cout << "YES\n";↵
for(int i = 0; i < m; i++)↵
{↵
int u = L[i]; int v = R[i];↵
ll d = dist1[u][v];↵
if(d <= 0) d = INF;↵
cout << u << ' ' << v << ' ' << d << '\n';↵
}↵
return 0;↵
}↵
bool tmp = dijkstra2();↵
if(!tmp)↵
{↵
cout << "NO\n";↵
return 0;↵
}↵
//cerr << d2[e] << '\n';↵
int cnt = 0;↵
while(!relax()) ↵
{↵
relax(); cnt++;↵
}↵
cerr << "RELAXATIONS DONE : " << cnt << '\n';↵
print();↵
}↵
~~~~~↵
</spoiler>↵
↵
<spoiler summary="Code (O(mlogn(logm+logL))">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<ll,ll> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int N = 1001;↵
const int M = 10001;↵
const ll INF = ll(1e18);↵
↵
int n, m, l, s, e;↵
↵
struct edge↵
{↵
int to; ll w; int label;↵
edge(int _to, int _w, int _label){to = _to, w = _w, label = _label;}↵
};↵
↵
int edgecnt = -1;↵
vector<edge> adj[N];↵
ll dist[N];↵
set<ii> used;↵
↵
ll dijk(int p, ll val)↵
{↵
for(int i = 0; i < n; i++) dist[i] = INF;↵
dist[s] = 0;↵
priority_queue<ii, vector<ii>, greater<ii> > pq;↵
pq.push(ii(0, s));↵
while(!pq.empty())↵
{↵
int u = pq.top().se; ll d = pq.top().fi; pq.pop();↵
for(int i = 0; i < adj[u].size(); i++)↵
{↵
edge tmp = adj[u][i];↵
int v = tmp.to; ll w = tmp.w; int lab = tmp.label;↵
if(lab >= 0)↵
{↵
if(lab < p) w = 1;↵
else if(lab == p) w = val;↵
else w = ll(1e14);↵
}↵
if(d + w < dist[v])↵
{↵
dist[v] = d + w;↵
pq.push(ii(dist[v], v));↵
}↵
}↵
}↵
return dist[e];↵
}↵
↵
void setw(int p, ll val)↵
{↵
for(int i = 0; i < n; i++)↵
{↵
for(int j = 0; j < adj[i].size(); j++)↵
{↵
int lab = adj[i][j].label;↵
if(lab >= 0)↵
{↵
if(lab < p)↵
{↵
adj[i][j].w = 1;↵
}↵
else if(lab == p)↵
{↵
adj[i][j].w = val;↵
}↵
else↵
{↵
adj[i][j].w = INF;↵
}↵
}↵
}↵
}↵
}↵
↵
void print()↵
{↵
cout << "YES\n";↵
for(int i = 0; i < n; i++)↵
{↵
for(int j = 0; j < adj[i].size(); j++)↵
{↵
edge tmp = adj[i][j];↵
int v = tmp.to; ll w = tmp.w; ↵
if(used.find(ii(i, v)) == used.end())↵
{↵
cout << i << ' ' << v << ' ' << w << '\n';↵
used.insert(ii(i, v)); used.insert(ii(v, i));↵
}↵
}↵
}↵
}↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
cin >> n >> m >> l >> s >> e;↵
for(int i = 0; i < m; i++)↵
{↵
int u, v, w;↵
cin >> u >> v >> w;↵
int lab = -1;↵
if(w == 0) ↵
{↵
lab = ++edgecnt;↵
}↵
adj[u].pb(edge(v, w, lab));↵
adj[v].pb(edge(u, w, lab));↵
}↵
ll x = dijk(edgecnt, 1); ll y = dijk(-1, 1);↵
if(!(x <= l && l <= y))↵
{↵
cout << "NO\n";↵
return 0;↵
}↵
ll lo = -1; ll hi = edgecnt;↵
ll mid, ans;↵
while(lo <= hi)↵
{↵
mid = (lo+hi)/2;↵
if(dijk(mid, 1) <= l)↵
{↵
ans = mid;↵
hi = mid - 1;↵
}↵
else↵
{↵
lo = mid + 1;↵
}↵
}↵
//now [0..ans] as 1 will give <= L whereas [0..ans - 1] as 1 will give > L↵
if(ans == -1)↵
{↵
setw(-1, 0);↵
print();↵
return 0;↵
}↵
lo = 1; hi = INF;↵
int ans2 = 0;↵
while(lo <= hi)↵
{↵
mid = (lo+hi)>>1;↵
if(dijk(ans, mid) <= l)↵
{↵
ans2 = mid;↵
lo = mid + 1;↵
}↵
else↵
{↵
hi = mid - 1;↵
}↵
}↵
//cerr << ans << ' ' << ans2 << '\n';↵
setw(ans, ans2);↵
print();↵
}↵
~~~~~↵
</spoiler>↵
↵
[Div. 2 E/Div. 1 C — Digit Tree](http://mirror.codeforces.com/contest/715/problem/C)↵
------------------↵
↵
Prerequisites : Tree DP, Centroid Decomposition, Math↵
↵
Compared to the other problems, this one is more standard. The trick is to first solve the problem if we have a fixed vertex $r$ as root and we want to find the number of paths passing through $r$ that works. This can be done with a simple tree dp. For each node $u$, compute the number obtained when going from $r$ down to $u$ and the number obtained when going from $u$ up to $r$, where each number is taken modulo $M$. This can be done with a simple dfs. To calculate the down value, just multiply the value of the parent node by $10$ and add the value on the edge to it. To calculate the up value, we also need to calculate the height of the node. (i.e. the distance from $u$ to $r$) Then, if we let $h$ be the height of $u$, $d$ be the digit on the edge connecting $u$ to its parent and $val$ be the up value of the parent of $u$, then the up value for $u$ is equal to $10^{h - 1} \cdot d + val$. Thus, we can calculate the up and down value for each node with a single dfs.↵
↵
Next, we have to figure out how to combine the up values and down values to find the number of paths passing through $r$ that are divisible by $M$. For this, note that each path is the concatenation of a path from $u$ to $r$ and $r$ to $v$, where $u$ and $v$ are pairs of vertices from different subtrees, and the paths that start from $r$ and end at $r$. For the paths that start and end at $r$ the answer can be easily calculated with the up and down values (just iterate through all nodes as the other endpoint). For the other paths, we iterate through all possible $v$, and find the number of vertices $u$ such that going from $u$ to $v$ will give a multiple of $M$. Since $v$ is fixed, we know its height and down value, which we denote as $h$ and $d$ respectively. So, if the up value of $u$ is equal to $up$, then $up \cdot 10^{h} + d$ must be a multiple of $M$. So, we can solve for $up$ to be $-d \cdot 10^{-h}$ modulo $M$. Note that in this case the multiplicative inverse of $10$ modulo $M$ is well-defined, as we have the condition $\gcd(M, 10) = 1$. To find the multiplicative inverse of $10$, we can find $\phi(M)$ and since by Euler's Formula we have $x^{\phi(M)} \equiv 1 (mod M)$ if $\gcd(x, M) = 1$, we have $x^{\phi(M) - 1} \equiv x^{-1} (mod M)$, which is the multiplicative inverse of $x$ (in this case we have $x = 10$) modulo $M$. After that, finding the $up$ value can be done by binary exponentiation.↵
↵
Thus, we can find the unique value of $up$ such that the path from $u$ to $v$ is a multiple of $M$. This means that we can just use a map to store the up values of all nodes and also the up values for each subtree. Then, to find the number of viable nodes $u$, find the required value of $up$ and subtract the number of suitable nodes that are in the same subtree as $v$ from the total number of suitable nodes. Thus, for each node $v$, we can find the number of suitable nodes $u$ in $O(\log MOD)$ time. ↵
↵
Now, we have to generalize this for the whole tree. We can use centroid decomposition. We pick the centroid as the root $r$ and find the number of paths passing through $r$ as above. Then, the other paths won't pass through $r$, so we can remove $r$ and split the tree into more subtrees, and recursively solve for each subtree as well. Since each subtree is at most half the size of the original tree, and the time taken to solve the problem where the path must pass through the root for a single tree takes time proportional to the size of the tree, this solution works in $O(n \log n(\log n + \log MOD))$ time, where the other $\log n$ comes from using maps.↵
↵
Time Complexity : $O(n \log n(\log n + \log MOD))$↵
↵
<spoiler summary="Code">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<int,int> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int N = 1e5 + 1;↵
const int MAX = 1e9;↵
int MOD, n;↵
↵
bool isprime[100001];↵
vector<ll> primes;↵
vector<ii> adj[N];↵
int subsize[N];↵
bool visited[N];↵
int treesize;↵
vi clrlist;↵
ll up[N];↵
ll down[N];↵
int h[N];↵
int PHI;↵
int dppart[N];↵
↵
ll mult(ll a, ll b)↵
{↵
return (a*b)%MOD;↵
}↵
↵
ll add(ll a, ll b)↵
{↵
return (a+b+MOD)%MOD;↵
}↵
↵
ll modpow(ll a, ll b)↵
{↵
ll r = 1;↵
while(b)↵
{↵
if(b&1) r=(r*a)%MOD;↵
a=(a*a)%MOD;↵
b>>=1;↵
}↵
return r;↵
}↵
↵
void Sieve(int n)↵
{↵
memset(isprime, 1, sizeof(isprime));↵
isprime[1] = false;↵
for(int i = 2; i <= n; i++)↵
{↵
if(isprime[i])↵
{↵
primes.pb(i);↵
for(int j = 2*i; j <= n; j += i)↵
{↵
isprime[j] = false;↵
}↵
}↵
}↵
}↵
↵
int phi(int n)↵
{↵
ll num = 1; ll num2 = n;↵
for(ll i = 0; primes[i]*primes[i] <= n; i++)↵
{↵
if(n%primes[i]==0)↵
{↵
num2/=primes[i];↵
num*=(primes[i]-1);↵
}↵
while(n%primes[i]==0)↵
{↵
n/=primes[i];↵
}↵
}↵
if(n>1)↵
{↵
num2/=n; num*=(n-1);↵
}↵
n = 1;↵
num*=num2;↵
return num;↵
}↵
↵
ll inv(ll a)↵
{↵
return modpow(a, PHI-1);↵
}↵
↵
void dfs(int u, int par)↵
{↵
if(par == -1) clrlist.clear();↵
subsize[u] = 1; clrlist.pb(u);↵
for(int i = 0; i < adj[u].size(); i++)↵
{↵
int v = adj[u][i].fi;↵
if(visited[v]) continue;↵
if(v == par) continue;↵
dfs(v, u);↵
subsize[u] += subsize[v];↵
} ↵
if(par == -1) treesize = subsize[u];↵
}↵
↵
int centroid(int u, int par)↵
{↵
for(int i = 0; i < adj[u].size(); i++)↵
{↵
int v = adj[u][i].fi;↵
if(visited[v]) continue;↵
if(v == par) continue;↵
if(subsize[v]*2 > treesize) return centroid(v, u);↵
}↵
return u;↵
}↵
↵
int parts = 0;↵
void fill(int u, int p, int cent)↵
{↵
if(p == cent)↵
{↵
dppart[u] = parts;↵
parts++;↵
}↵
else if(p != -1)↵
{↵
dppart[u] = dppart[p];↵
}↵
for(int i = 0; i < adj[u].size(); i++)↵
{↵
int v = adj[u][i].fi; int w = adj[u][i].se;↵
if(v == p || visited[v]) continue;↵
down[v] = add(mult(down[u], 10), w);↵
up[v] = add(up[u], mult(modpow(10, h[u]), w));↵
h[v] = h[u] + 1;↵
fill(v, u, cent);↵
//cout << v << ' ' << u << ' ' << up[v] << ' ' << up[u] << '\n';↵
}↵
}↵
↵
ll solve(int cent)↵
{↵
for(int i = 0; i < clrlist.size(); i++)↵
{↵
up[clrlist[i]] = 0; down[clrlist[i]] = 0; h[clrlist[i]] = 0;↵
}↵
parts = 0;↵
fill(cent, -1, cent); parts--;↵
dppart[cent] = -1; ↵
map<ll,ll> tot; //only count up↵
vector<map<ll,ll> > vec; //only count up, but in specific subtree↵
vec.resize(parts+1);↵
tot[0]++;↵
for(int i = 0; i < clrlist.size(); i++)↵
{↵
int u = clrlist[i];↵
//cout << u << ' ' << up[u] << ' ' << down[u] << '\n';↵
if(u == cent) continue;↵
tot[up[u]]++;↵
vec[dppart[u]][up[u]]++;↵
}↵
ll ans = 0;↵
for(int i = 0; i < clrlist.size(); i++)↵
{↵
int u = clrlist[i];↵
int ht = h[u];↵
int pt = dppart[u];↵
if(u == cent)↵
{↵
ans += (tot[0] - 1); //exclude cent as the vertex↵
}↵
else↵
{↵
ll val = ((-down[u])%MOD+MOD)%MOD;↵
val = mult(val, inv(modpow(10, ht)));↵
ans += (tot[val] - vec[pt][val]);↵
}↵
}↵
return ans;↵
}↵
↵
ll compsolve(int u)↵
{↵
dfs(u, -1);↵
int cent = centroid(u, -1);↵
ll ans = solve(cent);↵
//cout << u << ' ' << cent << ' ' << ans << '\n';↵
visited[cent] = true;↵
for(int i = 0; i < adj[cent].size(); i++)↵
{↵
int v = adj[cent][i].fi;↵
if(!visited[v]) ans += compsolve(v);↵
}↵
return ans;↵
}↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
cin >> n >> MOD;↵
if(MOD == 1)↵
{↵
cout << ll(n)*ll(n - 1);↵
return 0;↵
}↵
Sieve(100000); PHI = phi(MOD);↵
for(int i = 0; i < n - 1; i++) //tree is 0-indexed↵
{↵
int u, v, w; cin >> u >> v >> w;↵
adj[u].pb(ii(v, w)); adj[v].pb(ii(u, w));↵
}↵
cout << compsolve(0) << '\n';↵
return 0;↵
}↵
~~~~~↵
</spoiler>↵
↵
[Div. 1 D — Create a Maze](http://mirror.codeforces.com/contest/715/problem/D)↵
------------------↵
↵
Prerequisites : None↵
↵
The solution to this problem is quite simple, if you get the idea. Thanks to [user:dans,2016-09-17] for improving the solution to the current constraints which is much harder than my original proposal.↵
↵
Note that to calculate the difficulty of a given maze, we can just use dp. We write on each square (room) the number of ways to get from the starting square to it, and the number written on $(i, j)$ will be the sum of the numbers written on $(i - 1, j)$ and $(i, j - 1)$, and the edge between $(i - 1, j)$ and $(i, j)$ is blocked, we don't add the number written on $(i - 1, j)$ and similarly for $(i, j - 1)$. We'll call the rooms squares and the doors as edges. We'll call locking doors as edge deletions.↵
↵
First, we look at several attempts that do not work. ↵
↵
Write $t$ in its binary representation. To solve the problem, we just need to know how to construct a maze with difficulty $2x$ and $x + 1$ from a given maze with difficulty $x$. The most direct way to get from $x$ to $2x$ is to increase both dimensions of the maze by $1$. Let's say the bottom right square of the grid was $(n, n)$ and increased to $(n + 1, n + 1)$. So, the number $x$ is written at $(n, n)$. Then, we can block off the edge to the left of $(n + 1, n)$ and above $(n, n + 1)$. This will make the numbers in these two squares equal to $x$, so the number in square $(n + 1, n + 1)$ would be $2x$, as desired. To create $x + 1$ from $x$, we can increase both dimensions by $1$, remove edges such that $(n + 1, n)$ contains $x$ while $(n, n + 1)$ contains $1$ (this requires deleting most of the edges joining the $n$-th column and $(n + 1)$-th column. Thus, the number in $(n, n)$ would be $x + 1$. This would've used way too many edge deletions and the size of the grid would be too large. This was the original proposal.↵
↵
There's another way to do it with binary representation. We construct a grid with difficulty $2x$ and $2x + 1$ from a grid with difficulty $x$. The key idea is to make use of surrounding $1$s and maintaining it with some walls so that $2x + 1$ can be easily constructed. This method is shown in the picture below. This method would've used around $120 \times 120$ grid and $480$ edge deletions, which is too large to pass. ↵
↵
↵
↵
Now, what follows is the AC solution. Since it's quite easy once you get the idea, I recommend you to try again after reading the hint. To read the full solution, click on the spoiler tag.↵
↵
Hint : Binary can't work since there can be up to $60$ binary digits for $t$ and our grid size can be at most $50$. In our binary solution we used a $2 \times 2$ grid to multiply the number of ways by $2$. What about using other grid sizes instead?↵
↵
<spoiler summary="Full Solution">↵
Our AC solution uses base $6$ instead of binary. Write $t$ in base $6$. Note that $t$ has at most $24$ digits in base $6$, so to add a new digit we can increase the dimensions by $2$ and the number of deleted edges can be up to $12$ per digit. We'll construct such a way. This method is explained in the picture below. The key is to first construct a grid which has $0$ in it, then find a way to get $6x + i$ for all $0 \le i \le 5$ from $x$ by maintaining a wall of $1$s around the squares. This method uses a $50 \times 50 (2 \cdot 24 + 2 = 50)$ grid and at most $24 \cdot 12 + 2 = 290$ edge deletions and will get AC.↵
↵
↵
</spoiler>↵
↵
Of course, this might not be the only way to solve this problem. Can you come up with other ways of solving this or reducing the constraints even further? (Open Question)↵
↵
Time Complexity : $O(\log t)$↵
↵
<spoiler summary="Code">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<int,int> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int INF = 1e9 + 7;↵
const int MOD = 1e9 + 7;↵
↵
typedef pair<ii,ii> move;↵
↵
set<move> ans;↵
int curx, cury;↵
↵
bool isvalid(move x)↵
{↵
if(x.fi.fi > 0 && x.se.fi > 0 && x.fi.se > 0 && x.se.se > 0 && x.fi.fi <= curx && x.fi.se <= cury && x.se.fi <= curx && x.se.se <= cury) return true;↵
return false;↵
}↵
↵
void edge(int x1, int y1, int x2, int y2)↵
{↵
ans.insert(mp(mp(x1, y1), mp(x2, y2)));↵
}↵
↵
void add(int bit)↵
{↵
int x = curx;↵
edge(x,x+2,x,x+3);↵
edge(x+1,x+2,x+1,x+3);↵
edge(x+2,x,x+3,x);↵
edge(x+2,x+1,x+3,x+1);↵
edge(x-2,x+3,x-1,x+3);↵
edge(x,x+4,x+1,x+4);↵
edge(x+3,x-2,x+3,x-1);↵
edge(x+4,x,x+4,x+1);↵
edge(x-1,x+1,x,x+1);↵
if(bit%3==0) edge(x-1,x+2,x,x+2);↵
if(bit%3!=2) edge(x+2,x-1,x+2,x);↵
if(bit<3) edge(x+1,x-1,x+1,x);↵
curx += 2; cury += 2;↵
}↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
ll t; cin >> t;↵
vector<int> digits;↵
while(t)↵
{↵
digits.pb(t%6);↵
t/=6;↵
}↵
reverse(digits.begin(), digits.end());↵
edge(1, 2, 2, 2);↵
edge(2, 1, 2, 2);↵
curx = 2; cury = 2;↵
for(int i = 0; i < digits.size(); i++)↵
{↵
add(digits[i]);↵
}↵
cout << curx << ' ' << cury << '\n';↵
vector<move> clr;↵
for(set<move>::iterator it = ans.begin(); it != ans.end(); it++)↵
{↵
if(!isvalid(*it))↵
{↵
clr.pb(*it);↵
}↵
}↵
for(int i = 0; i < clr.size(); i++)↵
{↵
ans.erase(clr[i]);↵
}↵
cout << ans.size() << '\n';↵
for(set<move>::iterator it = ans.begin(); it != ans.end(); it++)↵
{↵
move tmp = (*it);↵
cout << tmp.fi.fi << ' ' << tmp.fi.se << ' ' << tmp.se.fi << ' ' << tmp.se.se << '\n';↵
}↵
}↵
~~~~~↵
</spoiler>↵
↵
[Div. 1 E — Complete The Permutations](http://mirror.codeforces.com/contest/715/problem/E)↵
------------------↵
↵
Prerequisites : Math, Graph Theory, DP, Any fast multiplication algorithm↵
↵
We'll slowly unwind the problem and reduce it to something easier to count. First, we need to determine a way to tell when the distance between $p$ and $q$ is exactly $k$. This is a classic problem but I'll include it here for completeness.↵
↵
Let $f$ denote the inverse permutation of $q$. So, the minimum number of swaps to transform $p$ into $q$ is the minimum number of swaps to transform $p_{f_{i}}$ into the identity permutation. Construct the graph where the edges are $i \rightarrow p_{f_{i}}$ for all $1 \le i \le n$. Now, note that the graph is equivalent to $q_{i} \rightarrow p_{i}$ and is composed of disjoint cycles after $q_{i}$ and $p_{i}$ are filled completely. Note that the direction of the edges doesn't matter so we consider the edges to be $p_{i} \rightarrow q_{i}$ for all $1 \le i \le n$. Note that if the number of cycles of the graph is $t$, then the minimum number of swaps needed to transform $p$ into $q$ would be $n - t$. (Each swap can break one cycle into two) This means we just need to find the number of ways to fill in the empty spaces such that the number of cycles is exactly $i$ for all $1 \le i \le n$.↵
↵
Now, some of the values $p_{i}$ and $q_{i}$ are known. The edges can be classified into four types : ↵
↵
A-type : The edges of the form $x \rightarrow ?$, i.e. $p_{i}$ is known, $q_{i}$ isn't.↵
↵
B-type : The edges of the form $? \rightarrow x$, i.e. $q_{i}$ is known, $p_{i}$ isn't.↵
↵
C-type : The edges of the form $x \rightarrow y$, i.e. both $p_{i}$ and $q_{i}$ are known.↵
↵
D-type : The edges of the form $? \rightarrow ?$, i.e. both $p_{i}$ and $q_{i}$ are unknown.↵
↵
Now, the problem reduces to finding the number of ways to assign values to the question marks such that the number of cycles of the graph is exactly $i$ for all $1 \le i \le n$. First, we'll simplify the graph slightly. While there exists a number $x$ appears twice (clearly it can't appear more than twice) among the edges, we will combine the edges with $x$ together to simplify the graph. If there's an edge $x \rightarrow x$, then we increment the total number of cycles by $1$ and remove this edge from the graph. If there is an edge $a \rightarrow x$ and $x \rightarrow b$, where $a$ and $b$ might be some given numbers or question marks, then we can merge them together to form the edge $a \rightarrow b$. Clearly, these are the only cases for $x$ to appear twice. Hence, after doing all the reductions, we're reduced to edges where each known number appears at most once, i.e. all the known numbers are distinct. We'll do this step in $O(n^2)$. For each number $x$, store the position $i$ such that $p_{i} = x$ and also the position $j$ such that $q_{j} = x$, if it has already been given and $-1$ otherwise. So, we need to remove a number when the $i$ and $j$ stored are both positive. We iterate through the numbers from $1$ to $n$. If we need to remove a number, we go to the two positions where it occur and replace the two edges with the new merged one. Then, recompute the positions for all numbers (takes $O(n)$ time). So, for each number, we used $O(n)$ time. (to remove naively and update positions) Thus, the whole complexity for this part is $O(n^2)$. (It is possible to do it in $O(n)$ with a simple dfs as well. Basically almost any correct way of doing this part that is at most $O(n^3)$ works, since the constraints for $n$ is low)↵
↵
Now, suppose there are $m$ edges left and $p$ known numbers remain. Note that in the end when we form the graph we might join edges of the form $a \rightarrow ?$ and $? \rightarrow b$ (where $a$ and $b$ are either fixed numbers or question marks) together. So, the choice for the $?$ can be any of the $m - p$ remaining unused numbers. Note that there will be always $m - p$ such pairs so we need to multiply our answer by $(m - p)!$ in the end. Also, note that the $?$ are distinguishable, and order is important when filling in the blanks.↵
↵
So, we can actually reduce the problem to the following : Given integers $a, b, c, d$ denoting the number of A-type, B-type, C-type, D-type edges respectively. Find the number of ways to create $k$ cycles using them, for all $1 \le k \le n$. Note that the answer is only dependent on the values of $a, b, c, d$ as the numbers are all distinct after the reduction.↵
↵
First, we'll look at how to solve the problem for $k = 1$. We need to fit all the edges in a single cycle. First, we investigate what happens when $d = 0$. Note that we cannot have a B-type and C-type edge before an A-type or C-type edge, since all numbers are distinct so these edges can't be joined together. Similarly, an A or C-type edge cannot be directly after a B or C-type edge. Thus, with these restrictions, it is easy to see that the cycle must contain either all A-type edges or B-type edges. So, the answer can be easily calculated. It is also important to note that if we ignore the cyclic property then a contiguous string of edges without D must be of the form AA...BB.. or AA...CBB..., where there is only one C, and zero or more As and Bs.↵
↵
Now, if $d \ge 1$, we can fix one of the D-type edges as the front of the cycle. This helps a lot because now we can ignore the cyclic properties. (we can place anything at the end of the cycle because D-type edges can connect with any type of edges) So, we just need to find the number of ways to make a length $n - 1$ string with $a$ As, $b$ Bs, $c$ Cs and $d - 1$ Ds. In fact, we can ignore the fact that the A-type edges, B-type edges, C-type edges and D-type edges are distinguishable and after that multiply the answer by $a!b!c!(d-1)!$.↵
↵
We can easily find the number of valid strings we can make. First, place all the Ds. Now, we're trying to insert the As, Bs and Cs into the $d$ empty spaces between, after and before the Ds. The key is that by our observation above, we only care about how many As, Bs and Cs we insert in each space since after that the way to put that in is uniquely determined. So, to place the As and Bs, we can use the balls in urns formula to find that the number of ways to place the As is $\binom{a + d - 1}{d - 1}$ and the number of ways to place the Bs is $\binom{b + d - 1}{d - 1}$. The number of ways to place the Cs is $\binom{d}{c}$, since we choose where the Cs should go.↵
↵
Thus, it turns out that we can find the answer in $O(1)$ (with precomputing binomial coefficients and factorials) when $k = 1$. We'll use this to find the answer for all $k$. In the general case, there might be cycles that consists entirely of As and entirely of Bs, and those that contains at least one D. We call them the A-cycle, B-cycle and D-cycles respectively. ↵
↵
Now, we precompute $f(n, k)$, the number of ways to form $k$ cycles using $n$ distinguishable As. This can be done with a simple dp in $O(n^3)$. We iterate through the number of As we're using for the first cycle. Then, suppose we use $m$ As. The number of ways to choose which of the $m$ As to use is $\binom{n}{m}$ and we can permute them in $(m - 1)!$ ways inside the cycle. (not $m!$ because we have to account for all the cyclic permutations) Also, after summing this for all $m$, we have to divide the answer by $k$, to account for overcounting the candidates for the first cycle (the order of the $k$ cycles are not important)↵
↵
Thus, $f(n, k)$ can be computed in $O(n^3)$. First, we see how to compute the answer for a single $k$. Fix $x, y, e, f$, the number of A-cycles, B-cycles, number of As in total among the A-cycles and number of Bs in total among the B-cycles. Then, since $k$ is fixed, we know that the number of D-cycles is $k - x - y$. Now, we can find the answer in $O(1)$. First, we can use the values of $f(e, x), f(f, y), f(d, k - x - y)$ to determine the number of ways to place the Ds, and the As, Bs that are in the A-cycles and B-cycles. Then, to place the remaining As, Bs and Cs, we can use the same method as we did for $k = 1$ in $O(1)$, since the number of spaces to place them is still the same. (You can think of it as each D leaves an empty space to place As, Bs and Cs to the right of it) After that, we multiply the answer by $\binom{a}{e} \cdot \binom{b}{f}$ to account for the choice of the set of As and Bs used in the A-only and B-only cycles. Thus, the complexity of this method is $O(n^4)$ for each $k$ and $O(n^5)$ in total, which is clearly too slow.↵
↵
We can improve this by iterating through all $x + y, e, f$ instead. So, for this to work we need to precompute $f(e, 0)f(f, x + y) + f(e, 1)f(f, x + y - 1) + ... + f(e, x + y)f(f, 0)$, which we can write as $g(x + y, e, f)$. Naively doing this precomputation gives $O(n^4)$. Then, we can calculate the answer by iterating through all $x + y, e, f$ and thus getting $O(n^3)$ per query and $O(n^4)$ for all $k$. This is still too slow to pass $n = 250$.↵
↵
We should take a closer look of what we're actually calculating. Note that for a fixed pair $e, f$, the values of $g(x + y, e, f)$ can be calculated for all possible $x + y$ in $O(n\log n)$ or $O(n^{1.58})$ by using Number Theoretic Transform or Karatsuba's Algorithm respectively. (note that the modulus has been chosen for NFT to work) This is because if we fix $e, f$, then we're precisely finding the coefficients of the polynomial $(f(e, 0)x^{0} + f(e, 1)x^{1} + ... + f(e, n)x^{n})(f(f, 0)x^{0} + f(f, 1)x^{1} + ... + f(f, n)x^{n})$, so this can be handled with NFT/Karatsuba.↵
↵
Thus, the precomputation of $g(x + y, e, f)$ can be done in $O(n^3\log n)$ or $O(n^{3.58})$.↵
↵
Next, suppose we fixed $e$ and $f$. We will calculate the answer for all possible $k$ in $O(n\log n)$ similar to how we calculated $g(x + y, e, f)$. This time, we're multiplying the following two polynomials : $f(d, 0)x^{0} + f(d, 1)x^{1} + ... + f(d, n)x^{n}$ and $g(0, e, f)x^{0} + g(1, e, f)x^{1} + ... + g(n, e, f)x^{n}$. Again, we can calculate this using any fast multiplication method, so the entire solution takes $O(n^3\log n)$ or $O(n^{3.58})$, depending on which algorithm is used to multiply polynomials.↵
↵
Note that if you're using NFT/FFT, there is a small trick that can save some time. When we precompute the values of $g(x + y, e, f)$, we don't need to do inverse FFT on the result and leave it in the FFTed form. After that, when we want to find the convolution of $f(d, i)$ and $g(i, e, f)$, we just need to apply FFT to the first polynomial and multiply them. This reduces the number of FFTs and it reduced my solution runtime by half.↵
↵
Time Complexity : $O(n^3\log n)$ or $O(n^{3.58})$, depending on whether NFT or Karatsuba is used.↵
↵
<spoiler summary="Code (NFT)">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<int,int> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int N = 251;↵
const int MOD = 998244353;↵
ll inv2;↵
ll prt;↵
ll iprt;↵
↵
ll dpncr[N][N];↵
ll fact[N];↵
ll inverse[N];↵
ll g[N][N];↵
ll sumg[N][N][N];↵
↵
vector<ii> perm;↵
int A, B, C, D;↵
↵
ll modpow(ll a, ll b)↵
{↵
ll r = 1;↵
while(b)↵
{↵
if(b&1) r = (r*a)%MOD;↵
a = (a*a)%MOD;↵
b>>=1;↵
}↵
return r;↵
}↵
↵
ll inv(ll a)↵
{↵
return modpow(a, MOD - 2);↵
}↵
↵
ll choose(int n, int m)↵
{↵
if(m < 0) return 0;↵
if(n < m) return 0;↵
if(m == 0) return 1;↵
if(n == m) return 1;↵
if(dpncr[n][m] != -1) return dpncr[n][m];↵
dpncr[n][m] = choose(n - 1, m - 1) + choose(n - 1, m);↵
dpncr[n][m] += MOD; dpncr[n][m] %= MOD;↵
return dpncr[n][m];↵
}↵
↵
void computefact()↵
{↵
fact[0] = 1;↵
for(ll i = 1; i < N; i++)↵
{↵
fact[i] = (fact[i - 1]*i)%MOD;↵
}↵
for(ll i = 1; i < N; i++)↵
{↵
inverse[i] = modpow(i, MOD - 2);↵
}↵
}↵
↵
void print(vector<ii>& vec)↵
{↵
for(int i = 0; i < vec.size(); i++)↵
{↵
cout << vec[i].fi << ' ' << vec[i].se << endl;↵
}↵
cout << "------------------------------------------------" << endl;↵
}↵
↵
void printans(vector<ll>& vec)↵
{↵
for(int i = 0; i < vec.size(); i++)↵
{↵
cout << vec[i] << ' ';↵
}↵
cout << endl;↵
}↵
↵
void printansi(vector<int>& vec)↵
{↵
for(int i = 0; i < vec.size(); i++)↵
{↵
cout << vec[i] << ' ';↵
}↵
cout << endl;↵
}↵
↵
void calcpos(vector<ii>& pos)↵
{↵
pos.resize(perm.size());↵
for(int i = 0; i < perm.size(); i++)↵
{↵
pos[i] = ii(-1, -1);↵
}↵
for(int i = 1; i < perm.size(); i++)↵
{↵
if(perm[i].fi > 0)↵
{↵
pos[perm[i].fi].fi = i;↵
}↵
if(perm[i].se > 0)↵
{↵
pos[perm[i].se].se = i;↵
}↵
}↵
}↵
↵
int reduce()↵
{↵
int n = perm.size() - 1;↵
vector<ii> pos;↵
int cnt = 0;↵
for(int i = 1; i <= n; i++) //Do a reduction↵
{↵
calcpos(pos);↵
//print(pos);↵
if(pos[i].fi > 0 && pos[i].se > 0)↵
{↵
if(pos[i].fi == pos[i].se) ↵
{↵
cnt++;↵
ii tmp1 = perm[pos[i].fi];↵
for(vector<ii>::iterator it = perm.begin(); it != perm.end(); it++)↵
{↵
if((*it) == tmp1)↵
{↵
perm.erase(it); break;↵
}↵
}↵
continue;↵
}↵
int p1 = pos[i].se; int l = perm[p1].fi; ii tmp1 = perm[p1];↵
int p2 = pos[i].fi; int r = perm[p2].se; ii tmp2 = perm[p2];↵
for(vector<ii>::iterator it = perm.begin(); it != perm.end(); it++)↵
{↵
if((*it) == tmp1)↵
{↵
perm.erase(it); break;↵
}↵
}↵
for(vector<ii>::iterator it = perm.begin(); it != perm.end(); it++)↵
{↵
if((*it) == tmp2)↵
{↵
perm.erase(it); break;↵
}↵
}↵
perm.pb(ii(l, r));↵
}↵
}↵
//count A, B, C, D↵
for(int i = 1; i < perm.size(); i++)↵
{↵
if(perm[i].fi > 0 && perm[i].se > 0)↵
{↵
assert(perm[i].fi != perm[i].se);↵
C++;↵
}↵
else if(perm[i].fi > 0)↵
{↵
A++;↵
}↵
else if(perm[i].se > 0)↵
{↵
B++;↵
}↵
else↵
{↵
D++;↵
}↵
}↵
return cnt;↵
}↵
↵
ll mult(ll a, ll b)↵
{↵
ll r = (a*b)%MOD;↵
r = (r+MOD)%MOD;↵
return r;↵
}↵
↵
ll add(ll a, ll b)↵
{↵
ll r = ((a+b)%MOD+MOD)%MOD;↵
return r;↵
}↵
↵
ll F(ll a, ll b, ll c, ll d)↵
{↵
ll ans = 1;↵
if(d == 0)↵
{↵
if(a == 0 && b == 0 && c == 0) return 1;↵
else return 0;↵
}↵
ans = mult(ans, fact[a]);↵
ans = mult(ans, fact[b]);↵
ans = mult(ans, fact[c]);↵
ans = mult(ans, choose(a+d-1, d-1));↵
ans = mult(ans, choose(b+d-1, d-1));↵
ans = mult(ans, choose(d, C));↵
return ans;↵
}↵
↵
const int LG = 9;↵
const int root_pw = (1<<LG);↵
void fft (vector<int> & a, bool invert) ↵
{↵
int n = (int) a.size();↵
↵
for (int i=1, j=0; i<n; ++i) {↵
int bit = n >> 1;↵
for (; j>=bit; bit>>=1)↵
j -= bit;↵
j += bit;↵
if (i < j)↵
swap (a[i], a[j]);↵
}↵
↵
for (int len=2; len<=n; len<<=1) {↵
int wlen = invert ? iprt : prt;↵
for (int i=len; i<root_pw; i<<=1)↵
wlen = int((wlen*1LL*wlen)%MOD);↵
for (int i=0; i<n; i+=len) {↵
int w = 1;↵
for (int j=0; j<len/2; ++j) {↵
int u = a[i+j]; int v = int((a[i+j+len/2]*1LL*w)%MOD);↵
a[i+j] = u+v < MOD ? u+v : u+v-MOD;↵
a[i+j+len/2] = u-v >= 0 ? u-v : u-v+MOD;↵
w = int (w * 1LL * wlen % MOD);↵
}↵
}↵
}↵
if (invert) {↵
ll nrev = inv(n);↵
for (int i=0; i<n; ++i)↵
a[i] = int((a[i]*1LL*nrev)%MOD);↵
}↵
}↵
↵
void multiply(vector<int>& a, vector<int>& b, vector<int>& res)↵
{↵
vector<int> fa(a.begin(), a.end()), fb(b.begin(), b.end());↵
int n = 1;↵
while(n < max(a.size(), b.size())) n <<= 1;↵
fa.resize(n); fb.resize(n);↵
//cerr << "A : "; printansi(fa); cerr << "B : "; printansi(fb);↵
fft(fa, 0); fft(fb, 0);↵
//cerr << "INVERT ONCE : ";↵
//printans(fa); printans(fb);↵
//fft(fa, 1); fft(fb, 1); cerr << "INVERT BACK A: "; printans(fa); cerr << "INVERT BACK B: "; printans(fb);↵
res.resize(n);↵
for(int i = 0; i < n; i++) res[i] = int((fa[i]*1LL*fb[i])%MOD);↵
//printans(fa);↵
fft(res, 1);↵
//cerr << "CONVOLUTION : "; printansi(res);↵
↵
}↵
↵
void computeg(int n)↵
{↵
g[0][0] = 1;↵
g[1][1] = 1;↵
for(int i = 2; i <= n; i++)↵
{↵
for(int j = 1; j <= i; j++)↵
{↵
for(int k = 1; k <= i; k++)↵
{↵
g[i][j] = add(g[i][j], mult(g[i-k][j-1], mult(choose(i, k), fact[k-1])));↵
}↵
//cerr << g[i][j] << '\n';↵
g[i][j] = mult(g[i][j], inverse[j]);↵
//cerr << "G : " << i << ' ' << j << ' ' << g[i][j] << '\n';↵
}↵
}↵
for(int i = 0; i <= A; i++)↵
{↵
for(int j = 0; j <= B; j++)↵
{↵
vector<int> gi; vector<int> gj;↵
gi.resize(n+1); gj.resize(n+1);↵
for(int k = 0; k <= n; k++)↵
{↵
gi[k] = int(g[i][k]);↵
gj[k] = int(g[j][k]);↵
//cerr << gi[k] << ' ' << gj[k] << '\n';↵
}↵
vector<int> res;↵
multiply(gi, gj, res);↵
for(int k = 0; k <= n; k++)↵
{↵
sumg[i][j][k] = res[k];↵
}↵
}↵
}↵
}↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
int n; cin >> n; perm.resize(n+1);↵
for(int i = 1; i <= n; i++)↵
{↵
cin >> perm[i].fi;↵
}↵
for(int i = 1; i <= n; i++)↵
{↵
cin >> perm[i].se;↵
}↵
ll tmpmult = 7*17;↵
tmpmult = mult(tmpmult, modpow(2, 23 - LG)); ↵
prt = modpow(3, tmpmult);↵
inv2 = inv(2);↵
iprt = inv(prt);↵
A = 0; B = 0; C = 0; D = 0;↵
memset(dpncr, -1, sizeof(dpncr));↵
memset(sumg, 0, sizeof(sumg));↵
memset(g, 0, sizeof(g));↵
memset(fact, 0, sizeof(fact));↵
memset(inverse, 0, sizeof(inverse));↵
int cycles = reduce();↵
computefact(); ↵
computeg(n);↵
//cerr << h(1, 0, 0) << endl;↵
↵
vector<ll> ans; ans.assign(n+1, 0);↵
↵
if(D - C < 0)↵
{↵
for(int i = 0; i < n; i++)↵
{↵
cout << ans[i] << ' ';↵
}↵
cout << endl;↵
return 0;↵
}↵
↵
for(int i = 0; i <= A; i++)↵
{↵
for(int j = 0; j <= B; j++)↵
{↵
ll coef = 1;↵
coef = mult(coef, F(A-i,B-j,C,D));↵
if(A > 0) coef = mult(coef, choose(A, i));↵
if(B > 0) coef = mult(coef, choose(B, j));↵
vector<int> gi; vector<int> gj;↵
gi.resize(n+1); gj.resize(n+1);↵
for(int k = 0; k <= n - cycles; k++)↵
{↵
gi[k] = int(g[D][k]);↵
gj[k] = int(sumg[i][j][k]);↵
}↵
vector<int> res;↵
multiply(gi, gj, res);↵
//cout << gi.size() << ' ' << gj.size() << ' ' << res.size() << ' ' << ans.size() << ' ' << n << ' ' << cycles << '\n';↵
for(int k = 0; k <= n - cycles; k++)↵
{↵
int moves = n - (k + cycles);↵
ans[moves] = add(ans[moves], mult(res[k], coef));↵
}↵
}↵
}↵
↵
for(int i = 0; i < ans.size(); i++)↵
{↵
ans[i] = mult(ans[i], fact[D-C]);↵
}↵
↵
for(int i = 0; i < n; i++)↵
{↵
cout << ans[i] << ' ';↵
}↵
cout << endl;↵
↵
return 0;↵
}↵
~~~~~↵
</spoiler>↵
↵
<spoiler summary="Code (Karatsuba)">↵
~~~~~↵
#include <bits/stdc++.h>↵
#include <ext/pb_ds/assoc_container.hpp>↵
#include <ext/pb_ds/tree_policy.hpp>↵
↵
using namespace std;↵
using namespace __gnu_pbds;↵
↵
#define fi first↵
#define se second↵
#define mp make_pair↵
#define pb push_back↵
#define fbo find_by_order↵
#define ook order_of_key↵
↵
typedef long long ll;↵
typedef pair<int,int> ii;↵
typedef vector<int> vi;↵
typedef long double ld; ↵
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;↵
typedef set<int>::iterator sit;↵
typedef map<int,int>::iterator mit;↵
typedef vector<int>::iterator vit;↵
↵
const int N = 251;↵
const int MOD = 998244353;↵
ll inv2;↵
ll prt;↵
ll iprt;↵
↵
ll dpncr[N][N];↵
ll fact[N];↵
ll inverse[N];↵
ll g[N][N];↵
ll sumg[N][N][N];↵
↵
vector<ii> perm;↵
int A, B, C, D;↵
↵
ll modpow(ll a, ll b)↵
{↵
ll r = 1;↵
while(b)↵
{↵
if(b&1) r = (r*a)%MOD;↵
a = (a*a)%MOD;↵
b>>=1;↵
}↵
return r;↵
}↵
↵
ll inv(ll a)↵
{↵
return modpow(a, MOD - 2);↵
}↵
↵
ll choose(int n, int m)↵
{↵
if(m < 0) return 0;↵
if(n < m) return 0;↵
if(m == 0) return 1;↵
if(n == m) return 1;↵
if(dpncr[n][m] != -1) return dpncr[n][m];↵
dpncr[n][m] = choose(n - 1, m - 1) + choose(n - 1, m);↵
dpncr[n][m] += MOD; dpncr[n][m] %= MOD;↵
return dpncr[n][m];↵
}↵
↵
void computefact()↵
{↵
fact[0] = 1;↵
for(ll i = 1; i < N; i++)↵
{↵
fact[i] = (fact[i - 1]*i)%MOD;↵
}↵
for(ll i = 1; i < N; i++)↵
{↵
inverse[i] = modpow(i, MOD - 2);↵
}↵
}↵
↵
void print(vector<ii>& vec)↵
{↵
for(int i = 0; i < vec.size(); i++)↵
{↵
cout << vec[i].fi << ' ' << vec[i].se << endl;↵
}↵
cout << "------------------------------------------------" << endl;↵
}↵
↵
void printans(vector<ll>& vec)↵
{↵
for(int i = 0; i < vec.size(); i++)↵
{↵
cout << vec[i] << ' ';↵
}↵
cout << endl;↵
}↵
↵
void printansi(vector<int>& vec)↵
{↵
for(int i = 0; i < vec.size(); i++)↵
{↵
cout << vec[i] << ' ';↵
}↵
cout << endl;↵
}↵
↵
void calcpos(vector<ii>& pos)↵
{↵
pos.resize(perm.size());↵
for(int i = 0; i < perm.size(); i++)↵
{↵
pos[i] = ii(-1, -1);↵
}↵
for(int i = 1; i < perm.size(); i++)↵
{↵
if(perm[i].fi > 0)↵
{↵
pos[perm[i].fi].fi = i;↵
}↵
if(perm[i].se > 0)↵
{↵
pos[perm[i].se].se = i;↵
}↵
}↵
}↵
↵
int reduce()↵
{↵
int n = perm.size() - 1;↵
vector<ii> pos;↵
int cnt = 0;↵
for(int i = 1; i <= n; i++) //Do a reduction↵
{↵
calcpos(pos);↵
//print(pos);↵
if(pos[i].fi > 0 && pos[i].se > 0)↵
{↵
if(pos[i].fi == pos[i].se) ↵
{↵
cnt++;↵
ii tmp1 = perm[pos[i].fi];↵
for(vector<ii>::iterator it = perm.begin(); it != perm.end(); it++)↵
{↵
if((*it) == tmp1)↵
{↵
perm.erase(it); break;↵
}↵
}↵
continue;↵
}↵
int p1 = pos[i].se; int l = perm[p1].fi; ii tmp1 = perm[p1];↵
int p2 = pos[i].fi; int r = perm[p2].se; ii tmp2 = perm[p2];↵
for(vector<ii>::iterator it = perm.begin(); it != perm.end(); it++)↵
{↵
if((*it) == tmp1)↵
{↵
perm.erase(it); break;↵
}↵
}↵
for(vector<ii>::iterator it = perm.begin(); it != perm.end(); it++)↵
{↵
if((*it) == tmp2)↵
{↵
perm.erase(it); break;↵
}↵
}↵
perm.pb(ii(l, r));↵
}↵
}↵
//count A, B, C, D↵
for(int i = 1; i < perm.size(); i++)↵
{↵
if(perm[i].fi > 0 && perm[i].se > 0)↵
{↵
assert(perm[i].fi != perm[i].se);↵
C++;↵
}↵
else if(perm[i].fi > 0)↵
{↵
A++;↵
}↵
else if(perm[i].se > 0)↵
{↵
B++;↵
}↵
else↵
{↵
D++;↵
}↵
}↵
return cnt;↵
}↵
↵
ll mult(ll a, ll b)↵
{↵
ll r = (a*b)%MOD;↵
r = (r+MOD)%MOD;↵
return r;↵
}↵
↵
ll add(ll a, ll b)↵
{↵
ll r = ((a+b)%MOD+MOD)%MOD;↵
return r;↵
}↵
↵
ll F(ll a, ll b, ll c, ll d)↵
{↵
ll ans = 1;↵
if(d == 0)↵
{↵
if(a == 0 && b == 0 && c == 0) return 1;↵
else return 0;↵
}↵
ans = mult(ans, fact[a]);↵
ans = mult(ans, fact[b]);↵
ans = mult(ans, fact[c]);↵
ans = mult(ans, choose(a+d-1, d-1));↵
ans = mult(ans, choose(b+d-1, d-1));↵
ans = mult(ans, choose(d, C));↵
return ans;↵
}↵
↵
ll buffer[20001], bufferpos, siz = 1024;↵
const int LG = 4;↵
↵
void multiply(int size, ll a[], ll b[], ll r[])↵
{↵
if(size <= (1<<LG))↵
{↵
for(int i = 0; i < size*2; i++) r[i] = 0;↵
for(int i = 0; i < size; i++)↵
{↵
if(a[i])↵
{↵
for(int j = 0; j < size; j++)↵
{↵
r[i+j] += a[i]*b[j];↵
r[i+j] %= MOD;↵
}↵
}↵
}↵
for(int i = 0; i < size*2; i++)↵
{↵
r[i] %= MOD;↵
}↵
return ;↵
}↵
int s = size/2;↵
multiply(s, a, b, r);↵
multiply(s, a+s, b+s, r+size);↵
ll *a2 = buffer+bufferpos; bufferpos += s;↵
ll *b2 = buffer+bufferpos; bufferpos += s;↵
ll *r2 = buffer+bufferpos; bufferpos += size;↵
for(int i = 0; i < s; i++)↵
{↵
a2[i] = a[i] + a[i+s];↵
if(a2[i]>=MOD) a2[i]-=MOD;↵
}↵
for(int i = 0; i < s; i++)↵
{↵
b2[i] = b[i] + b[i+s];↵
if(b2[i]>=MOD) b2[i]-=MOD;↵
}↵
multiply(s, a2, b2, r2);↵
for(int i = 0; i < size; i++)↵
{↵
r2[i] -= (r[i] + r[i+size]);↵
}↵
for(int i = 0; i < size; i++)↵
{↵
r[i+s] += r2[i];↵
r[i+s]%=MOD;↵
if(r[i+s]<0) r[i+s]+=MOD;↵
}↵
bufferpos -= (s+s+size);↵
}↵
ll gi[N+5]; ll gj[N+5];↵
↵
void computeg(int n)↵
{↵
g[0][0] = 1;↵
g[1][1] = 1;↵
for(int i = 2; i <= n; i++)↵
{↵
for(int j = 1; j <= i; j++)↵
{↵
for(int k = 1; k <= i; k++)↵
{↵
g[i][j] = add(g[i][j], mult(g[i-k][j-1], mult(choose(i, k), fact[k-1])));↵
}↵
g[i][j] = mult(g[i][j], inverse[j]);↵
}↵
}↵
for(int i = 0; i <= A; i++)↵
{↵
for(int j = 0; j <= B; j++)↵
{↵
siz = 512;↵
while(siz/2 >= n+1) siz>>=1;↵
for(int k = 0; k < siz; k++)↵
{↵
if(k <= n)↵
{↵
gi[k] = g[i][k];↵
gj[k] = g[j][k];↵
}↵
else↵
{↵
gi[k] = gj[k] = 0;↵
}↵
}↵
ll *res = buffer+bufferpos;↵
bufferpos+=2*siz;↵
multiply(siz,gi,gj,res);↵
for(int k = 0; k <= n; k++)↵
{↵
sumg[i][j][k] = res[k];↵
}↵
bufferpos-=2*siz;↵
}↵
}↵
}↵
↵
int main()↵
{↵
ios_base::sync_with_stdio(0); cin.tie(0);↵
int n; cin >> n; perm.resize(n+1);↵
↵
for(int i = 1; i <= n; i++)↵
{↵
cin >> perm[i].fi;↵
}↵
for(int i = 1; i <= n; i++)↵
{↵
cin >> perm[i].se;↵
}↵
↵
A = 0; B = 0; C = 0; D = 0;↵
memset(dpncr, -1, sizeof(dpncr));↵
memset(sumg, 0, sizeof(sumg));↵
memset(g, 0, sizeof(g));↵
memset(fact, 0, sizeof(fact));↵
memset(inverse, 0, sizeof(inverse));↵
int cycles = reduce();↵
computefact(); computeg(n);↵
vector<ll> ans; ans.assign(n+1, 0);↵
↵
if(D - C < 0)↵
{↵
for(int i = 0; i < n; i++)↵
{↵
cout << ans[i] << ' ';↵
}↵
cout << endl;↵
return 0;↵
}↵
↵
for(int i = 0; i <= A; i++)↵
{↵
for(int j = 0; j <= B; j++)↵
{↵
ll coef = 1;↵
coef = mult(coef, F(A-i,B-j,C,D));↵
if(A > 0) coef = mult(coef, choose(A, i));↵
if(B > 0) coef = mult(coef, choose(B, j));↵
siz = 512;↵
while(siz/2 >= n-cycles+1) siz>>=1;↵
for(int k = 0; k < siz; k++)↵
{↵
if(k <= n-cycles)↵
{↵
gi[k] = g[D][k];↵
gj[k] = sumg[i][j][k];↵
}↵
else↵
{↵
gi[k] = gj[k] = 0;↵
}↵
}↵
ll *res = buffer+bufferpos;↵
bufferpos+=2*siz;↵
multiply(siz,gi,gj,res);↵
for(int k = 0; k <= n - cycles; k++)↵
{↵
int moves = n - (k + cycles);↵
ans[moves] = add(ans[moves], mult(res[k], coef));↵
}↵
bufferpos-=2*siz;↵
}↵
}↵
↵
for(int i = 0; i < ans.size(); i++)↵
{↵
ans[i] = mult(ans[i], fact[D-C]);↵
}↵
↵
for(int i = 0; i < n; i++)↵
{↵
cout << ans[i] << ' ';↵
}↵
cout << endl;↵
}↵
~~~~~↵
</spoiler>↵
↵





