Hi everyone!

Thank you for joining Weekly Training Farm 19. The solution codes will be uploaded later.

Congratulations to:

• The winner: zscoder
• The runner up: eddy1021
• 3rd place: arosusti

Problem A. Aligned Text

This problem is equivalent to finding the longest arithmetic progression of a given set S. We can always enumerate the common difference w and use another loop to find the maximum length.

Problem B. Bitcount

If we want to count something that can be represented as a sum of values taken within an interval [a, b], we can always translate them as count([a, b]) = count([0, b]) - count([0, a - 1]). Usually this will make the implementation easier (and safer).

Moreover, in this problem, we can even deal with each binary digit separately. Hence, given an upper bound m ( = b or  = a - 1) and a position 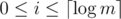, we can focus on counting the number of 1-bits in the i-th position between 1 and m.

Problem C. Crossing River

There are "forward" methods and "reversed" methods. The "forward" idea is to identify dp[i] to be the smallest possible jumping gap from the left river bank to the i-th rock. However, the table is not easy to build in time. Although I believe it is achievable using set iterators, but no one use it during the contest =)

The key to this problem is to use the "reversed" idea: binary search. We first guess an answer m and then decide if the frog can cross the river with jumping distance no more than m. There are several way to do this. The first idea (coincident to the author's solution) is to use the sliding window technique: keeping all reachable rocks within the range [i - m, i - 1]. If any of these rocks has value less or equal to a_i, then the i-th stone is reachable. We can use a deque to achieve linear time testing given m.

The second idea is to first sort the rocks according to their values: we don't need sliding windows anymore! We use sliding ubuntu! Then, we greedily consider each rock in the order of their values, if we can jump furtherer, we jump. This solution is simpler and looks elegant to me.

• There are other solutions uses BIT or sets, make acceptable 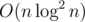solutions.

Problem D. Dice Rolling

Tricky case-study problem. Define the opposite faces as a "set". The key to this problem is the following lemma:

Lemma: Let {l, r} be a "set". In any dice rolling sequence, between two occurrence of l there must exist an r.

So, let the sum be the sum of two numbers in a "set", the answer must be a multiple of sum plus some remaining extra (at most three) larger number in some sets. So the special cases started by studying n = 1 or m = 1, then n = 2 or m = 2, then n ≥ 3 and m ≥ 3. The very special case is when (n, m) = (2, 4) or (4, 2).

Problem E. Escaped String

At first glance, it seems to be a classical O(n²) dynamic programming: dp[i][j] is defined to be the shortest possible length of subsequence s of A[0..i] and the first occurrence in string B as a subsequence ending at j-th character. Then we have the following:

• dp[i][j] = dp[i - 1][j], if A[i] ≠ B[j].
• dp[i][j] = min{dp[i - 1][j], dp[i - 1][prev_B(j - 1, A[i - 1])]}, if A[i] = B[j], where prev_B(j - 1, A[i - 1]) is the previous occurrence of A[i - 1] appear in string B before index j - 1.

However, this needs an O(n²) size memory, which is unaffordable. By observing that the dynamic programming state is meaningful only when A[i] = B[j], we can use a memory efficient encoding for storing these DP states. Please refer to My code for implementation.

The second solution is to notice that the answer is always less or equal to 1 +  the maximum occurrence of any single letter (i.e.,  ≤ 501). This is because one can greedily choose the character α such that the index that the "next α" occurring in A  ≤  the index of the "next α" occurring in B, among these character we choose the largest indexed α in B. It gives us a solution of length no more than 501. Now, we can use the LIS idea: let 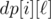to be the largest index j in B such that there exists a subsequence of A[0..i] of length 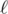occurs in B[0..j] but not B[0..j - 1].

Then the recurrence relation is: 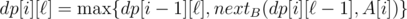.