Hi I'm having trouble with the 2-CNF (Conjuctive Normal Form) problem, not just 2-SAT but the more general case of Conjuctive Normal Forms, ie: a => b (a implies b), c => ¬d (c implies not d). I've got some doubts, if you can help me with any of them it would help me a lot.
1 — What is the answer for the case (a => b) and (b => ¬a) and (¬a => c) and (c => d) and (d => ¬c)? I think its not satisfiable but if you solve like 2-SAT by just checking for all x if x and ¬x are in the same SCC then getting the variable with higher toposort between (x and ¬x) as the answer you may get another answer.
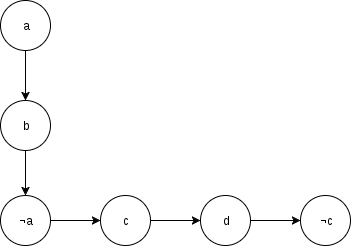
2 — There is an algorithm to find if some 2-CNF is solvable? And if its solvable how can we get some solution?
3 — If x or ¬x has no in edge nor out edge in the graph of implications, its correct to just set it as the answer? If you just get the toposort values like in 2-SAT algorithms, x or ¬x can be set as answer depending of how you do the toposort, but in some cases I think it doenst work.
Ex: (a => b) and (b => ¬a) and (¬a => c). If we dont treat it the toposort of ¬c can be grater than toposort of c and ¬c may be setted as the answer, but it is mandatory that ¬a is in the answer so c is in the answer.
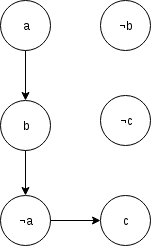
4 — There is a way to calculate the total number of ways of chose the values of variables to get a satisfiable solution?






