We were waiting several weeks to setting this contest and hope the problem was good enough.
Events
There was a difficulty with 805E - Раскраска мороженого/804C - Раскраска мороженого. A little bug in the checker fortunately yields accepting an incorrect solution of only one person during the contest. I should apologize all of you because of this.
For this sentence, Vertices which have the i-th (1 ≤ i ≤ m) type of ice cream form a connected subgraph. You can find the meaning of "connected subgraph" with connected and subgraph, thus it can be empty as it is more logical. How ever, I should apologize all of the participants because of weak sample tests in the statement.
I will write the full editorial in the few next days, now some hints and short solutions exist here.
Hints
Almost half of numbers are divisible by two.
For the string shouldn't be any i ≤ n - 2, si = si + 2. Make some examples of little sizes.
805C - Найти Амира / 804A - Найти Амира
Find minimum weighted edges.
There is some edges with weight 0, try to connect them in a carefully way.
805D - Минимальное число шагов / 804B - Минимальное число шагов
The last situation is some 'a' characters after some 'b' ones.
The last situation is unique.
The number of steps is also unique.
Each 'b' character makes a number of 'b' characters in the last situation according to the number of 'a' characters before it.
805E - Раскраска мороженого / 804C - Раскраска мороженого
We want to color the ice creams in a way that all of ice creams in a vertex would be different with this condition that if two vertices u and v have ice cream i, then all of vertices in the unique path of u and v would have it.
Let's have a trivial lower-bound for the answer.
The trivial lower-bound should be maximum size of vertices' sets.
You can prove that by induction on leaves of the tree. And code it how you proved it.
805F - Матожидание диаметра дерева / 804D - Матожидание диаметра дерева
Let's solve the problem for just two tree.
dt is diameter of t-th tree and fi is the maximum path starting from vertex i, for all valid i and j, assume that the edge is between them and find the diameter with max(fi + fj + 1, max(d1, d2)).
consider this trivial 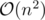 solution and try to improve it to
solution and try to improve it to 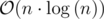 .
.
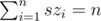
seems SQRT.
For every new query, try to do it with the complexity of 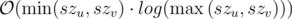 , which szi means size of the components of i-th vertex. Prove its complexity is
, which szi means size of the components of i-th vertex. Prove its complexity is 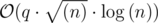 .
.
You can prove, we need even number of swaps to reach the same permutation. So 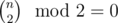 and the answer for 4·k + 3 and 4·k + 4 is -1.
and the answer for 4·k + 3 and 4·k + 4 is -1.
The solution almost is constructive.
And then solve n = 8 by n = 4.
Let's partition n = 4·k numbers to classes, each class contains a 4 consecutive numbers. And when n = 4·k + 1 there is a class with 5 consecutive numbers.
The problem consists two parts, the first part is to find mni and mxi, the minimum and the maximum score i-th vertex may get after the score distribution. The second part is to finding the answer and all your need to solve this part is those two arrays. It is trivial mni is number of real bullion of golds in i-th vertex.
Let's find the scores for two vertices u and v, u have a directed edge to v.
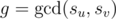
If i-th element from u-th vertex was painted and j-th element from v-th vertex was unpainted such that 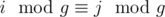 then j-th element from v-th vertex will be painted quickly. For two vertex, we can do it in complexity
then j-th element from v-th vertex will be painted quickly. For two vertex, we can do it in complexity 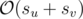 .
.
If we have this directed walk {w1, w2, ..., wk}, you should affect v1 on vk how I said in the previous hint with 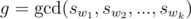 .
.
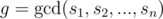
In this components if i-th element from u-th vertex was painted then for all of j such that 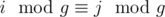 , j-th element from all vertices will be painted quickly. For this components, we can do it with complexity
, j-th element from all vertices will be painted quickly. For this components, we can do it with complexity 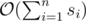 . In the main problem, we can suppose all of a strongly conected component a vertex with size g in this way and we can calculate mxi with answer of its component's vertex multiplied by
. In the main problem, we can suppose all of a strongly conected component a vertex with size g in this way and we can calculate mxi with answer of its component's vertex multiplied by 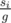 .
.
SCC of the tournament yields a Hamiltonian path of strongly connected components( if we consider each component a vertex ). The problem decreased to solve this path. we can solve the path with the complexity of sum of vertices' sizes.
Now, for every vertex we have minimum and maximum score it may get. For B known vertices, to check if they can be the wanted set, we can assume their score be maximum possible and the other scores be minimum possible. If they were top, then they can be a sample of the wanted set.
Consider a sorted sequence of combination of two array mn and mx.
For every vertex, consider the number of ways it(with its maximum score) can be the minimum score of the set of B vertices.
Solutions
Time Complexity: 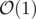
Memory complexity: 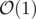
l,r=list(map(int,input().split()))
print(2 if l<r else l)
int main(){
int l, r;
scanf("%d%d", &l, &r);
printf("%d", l == r ? l : 2);
}
Time Complexity: 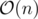
Memory complexity: 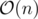
print(("aabb" * 50000)[:int(input())])
int N;
int main()
{
scanf("%d", &N);
for (int i = 0; i < N; i++)
putchar(i & 2 ? 'b' : 'a');
puts("");
}
Time Complexity: 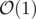
Memory complexity: 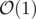
print((int(input())-1)//2)
int main(){
int n;
scanf("%d", &n);
printf("%d\n", (n-1)/2);
}
Time Complexity: 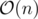
Memory complexity: 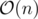
s = input()
cnt = 0
m=10**9 + 7
t = 0
for i in range(len(s)):
if s[~i] == 'a':
cnt = (cnt+t)%m
t = (t*2)%m
else:
t += 1
print(cnt)
int c,d,i,n,m,k,x,j=1000000007;
string s;
main(){
cin>>s;
for(i=s.size()-1;i>=0;i--){
if(s[i]=='b')c++;else{
k+=c;c*=2;k%=j;c%=j;
}
}
cout<<k;
}
Time Complexity: 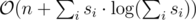
Memory complexity: 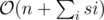
// +-- -- --++-- +-In the name of ALLAH-+ --++-- -- --+ \\
int const N = 3e5 + 10 ;
int n , m , ans = 1 , res[N] ;
vector <int> g[N] , vec[N] ;
inline bool cmp (int a , int b) {
return res[a] < res[b] ;
}
void dfs (int v , int par = -1) {
int col = ans , p = (int)vec[v].size() - 1 ;
sort(vec[v].begin() , vec[v].end() , cmp) ;
for (int x : vec[v]) {
if (res[x]) {
continue ;
}
while (p >= 0 && col == res[vec[v][p]]) {
col -- ;
p -- ;
}
res[x] = col ;
col -- ;
}
for (int u : g[v]) {
if (u != par) {
dfs(u , v) ;
}
}
}
int main(){
ios::sync_with_stdio(false) , cin.tie(0) , cout.tie(0) ;
cin >> n >> m ;
for (int i = 0 ; i < n ; i ++) {
int sz ;
cin >> sz ;
ans = max(ans , sz) ;
while (sz --) {
int x ;
cin >> x ;
x -- ;
vec[i].push_back(x) ;
}
}
for (int i = 0 ; i < n - 1 ; i ++) {
int u , v ;
cin >> u >> v ;
u -- , v -- ;
g[u].push_back(v) ;
g[v].push_back(u) ;
}
dfs(0) ;
cout << ans << '\n' ;
for (int i = 0 ; i < m ; i ++) {
cout << max(res[i] , 1) << ' ' ;
}
cout << '\n' ;
}
Time Complexity: 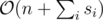
Memory complexity: 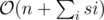
vector <int> Vs[300050];
vector <int> conn[300050];
int ans[300050];
bool chk[500050];
bool dchk[300050];
vector <int> Vu;
void DFS(int n) {
dchk[n] = true;
for (auto it : Vs[n]) {
if (ans[it]) chk[ans[it]] = true;
else Vu.push_back(it);
}
int a = 1;
for (auto it : Vu) {
while (chk[a]) a++;
ans[it] = a++;
}
for (auto it : Vs[n]) chk[ans[it]] = false;
Vu.clear();
for (auto it : conn[n]) {
if (dchk[it]) continue;
DFS(it);
}
}
int main() {
int N, M, i;
scanf("%d %d", &N, &M);
for (i = 1; i <= N; i++) {
int t1, t2;
scanf("%d", &t1);
while (t1--) {
scanf("%d", &t2);
Vs[i].push_back(t2);
}
}
for (i = 1; i < N; i++) {
int t1, t2;
scanf("%d %d", &t1, &t2);
conn[t1].push_back(t2);
conn[t2].push_back(t1);
}
DFS(1);
int mx = 0;
for (i = 1; i <= M; i++) {
mx = max(mx, ans[i]);
if (ans[i] == 0) ans[i] = 1;
}
mx = max(mx, 1);
printf("%d\n", mx);
for (i = 1; i <= M; i++) printf("%d ", ans[i]);
return !printf("\n");
}
Time Complexity: 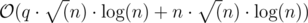
Memory complexity: 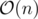
using namespace std ;
#define int long long
const int MAXN = 1e5 + 100 ;
vector<int>ver[MAXN] , com[MAXN] , ps[MAXN] ;
int vis[MAXN] , dis[MAXN] ;
int mxr , mxid ;
void dfs(int v , int col = -1 , int h = 0 , int par = -1){
vis[v] = max(vis[v] , col) ;
if(mxr < h)mxid = v , mxr = h ;
dis[v] = max(h , dis[v]) ;
if(col > 0)com[col] . push_back(dis[v]) ;
for(auto u : ver[v]){
if(u == par)continue ;
dfs(u , col , h + 1 , v) ;
}
}
map<pair<int , int> , int> check ;
int32_t main(){
ios_base::sync_with_stdio(0) ;
cin . tie(0) ; cout . tie(0) ;
int n , m , q ; cin >> n >> m >> q ;
for(int i = 0 ; i < m ; i ++){
int x , y ; cin >> x >> y ;
x -- , y -- ;
ver[x] . push_back(y) ;
ver[y] . push_back(x) ;
}
int cnt = 0 ;
for(int i = 0 ; i < n ; i ++){
if(vis[i])continue ;
mxr = 0 , mxid = i ;
dfs(i) ;
mxr = 0 ;
dfs(mxid) ;
dfs(mxid , ++ cnt) ; sort(com[cnt] . begin() , com[cnt] . end()) ;
ps[cnt] . push_back(0) ;
for(auto v : com[cnt])ps[cnt] . push_back(ps[cnt] . back() + v) ;
}
cout << fixed << setprecision(10) ;
while(q --){
int x , y ; cin >> x >> y ;
x -- , y -- ; x = vis[x] ; y = vis[y] ;
if(com[x] . size() > com[y] . size())swap(x , y) ;
if(x == y){cout << -1 << '\n' ; continue ; }
if(check[{x , y}] > 0){cout << double(check[{x , y}]) / (1ll * com[x] . size() * com[y] . size()) << '\n' ; continue ; }
int ans = 0 , mxd = max(com[x] . back() , com[y] . back()) ;
for(auto v : com[x]){
int num = lower_bound(com[y] . begin() , com[y] . end() , mxd - v - 1) - com[y] . begin() ;
ans += num * mxd + (com[y] . size() - num) * (v + 1) + ps[y] . back() - ps[y][num] ;
}
check[{x , y}] = ans ;
cout << double(check[{x , y}]) / (1ll * com[x] . size() * com[y] . size()) << '\n' ;
}
}
Time Complexity: 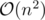
Memory complexity: 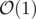
int n;
int main()
{
scanf("%d",&n);
if(n%4>1)return printf("NO\n"),0;
printf("YES\n");
for(int i=1;i<n;i+=4)
{
if(n%4)printf("%d %d\n%d %d\n%d %d\n",i+2,n,i+2,i+3,i+3,n);
else printf("%d %d\n",i+2,i+3);
printf("%d %d\n",i,i+2);
printf("%d %d\n",i+1,i+3);
printf("%d %d\n",i+1,i+2);
printf("%d %d\n",i,i+3);
if(n%4)printf("%d %d\n%d %d\n%d %d\n",i,n,i,i+1,i+1,n);
else printf("%d %d\n",i,i+1);
}
for(int i=1;i<n;i+=4)
for(int j=i+4;j<n;j+=4)
{
printf("%d %d\n",i+3,j+2);
printf("%d %d\n",i+2,j+2);
printf("%d %d\n",i+3,j+1);
printf("%d %d\n",i,j+1);
printf("%d %d\n",i+1,j+3);
printf("%d %d\n",i+2,j+3);
printf("%d %d\n",i+1,j+2);
printf("%d %d\n",i+1,j+1);
printf("%d %d\n",i+3,j);
printf("%d %d\n",i+3,j+3);
printf("%d %d\n",i,j+2);
printf("%d %d\n",i,j+3);
printf("%d %d\n",i+2,j);
printf("%d %d\n",i+2,j+1);
printf("%d %d\n",i+1,j);
printf("%d %d\n",i,j);
}
return 0;
}
Time Complexity: 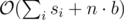
Memory complexity: 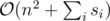
import java.io.OutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStream;
import java.io.PrintWriter;
import java.io.BufferedWriter;
import java.util.InputMismatchException;
import java.io.IOException;
import java.util.Stack;
import java.util.ArrayList;
import java.util.List;
import java.util.stream.Stream;
import java.util.Vector;
import java.io.Writer;
import java.io.OutputStreamWriter;
import java.util.BitSet;
import java.io.InputStream;
/**
* Built using CHelper plug-in
* Actual solution is at the top
*/
public class Main {
public static void main(String[] args) {
InputStream inputStream = System.in;
OutputStream outputStream = System.out;
InputReader in = new InputReader(inputStream);
OutputWriter out = new OutputWriter(outputStream);
TaskF solver = new TaskF();
solver.solve(1, in, out);
out.close();
}
static class TaskF {
public int mod = 1000000007;
public int n;
public int a;
public int b;
public char[][] adj;
public List<Integer>[] graph;
public void solve(int testNumber, InputReader in, OutputWriter out) {
n = in.nextInt();
a = in.nextInt();
b = in.nextInt();
adj = new char[n][n];
graph = Stream.generate(ArrayList::new).limit(n).toArray(List[]::new);
for (int i = 0; i < n; i++) adj[i] = in.next().toCharArray();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (adj[i][j] == '1') {
graph[i].add(j);
}
}
}
List<List<Integer>> comp = new SCCTarjan().scc(graph);
boolean[][] can = new boolean[n][];
int[] low = new int[n];
for (int i = 0; i < n; i++) {
int q = in.nextInt();
char[] w = in.next().toCharArray();
can[i] = new boolean[q];
for (int j = 0; j < q; j++) {
can[i][j] = w[j] == '1';
if (can[i][j]) low[i]++;
}
}
int[] wcomp = new int[n];
int idx = 0;
List<BitSet> bb = new ArrayList<>();
List<Integer> bs = new ArrayList<>();
for (List<Integer> gg : comp) {
int gcd = 0;
for (int x : gg) {
gcd = Utils.gcd(gcd, can[x].length);
wcomp[x] = idx;
}
idx++;
BitSet d = new BitSet(gcd);
bs.add(gcd);
bb.add(d);
for (int x : gg) {
for (int i = 0; i < can[x].length; i++) {
if (can[x][i]) {
d.set(i % gcd, true);
}
}
}
}
for (int kk = comp.size() - 1; kk > 0; kk--) {
int g = Utils.gcd(bs.get(kk), bs.get(kk - 1));
BitSet ww = new BitSet(g);
for (int i = 0; i < bs.get(kk); i += g) {
ww.or(bb.get(kk).get(i, i + g));
}
for (int i = 0; i < bs.get(kk - 1); i++) {
if (ww.get(i % g)) {
bb.get(kk - 1).set(i, true);
}
}
}
int[] high = new int[n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < can[i].length; j++) {
if (bb.get(wcomp[i]).get(j % bs.get(wcomp[i])))
high[i]++;
}
}
long ret = 0;
int[][] comb = Utils.getComb(n + 1, mod);
for (int lowest = 0; lowest < n; lowest++) {
int countabove = 0;
for (int other = 0; other < n; other++) {
if (other == lowest) continue;
if (low[other] > high[lowest]) {
countabove++;
}
}
if (countabove >= a) {
continue;
}
int canbig = 0;
for (int other = 0; other < n; other++) {
if (other == lowest) continue;
if (low[other] <= high[lowest] && (high[other] > high[lowest] || (high[other] == high[lowest] && other > lowest))) {
canbig++;
}
}
for (int take = 0; take < b && take <= canbig && take + countabove < a; take++) {
ret = (ret + 1L * comb[canbig][take] * comb[countabove][b - take - 1]) % mod;
}
}
out.println(ret);
}
}
static class OutputWriter {
private final PrintWriter writer;
public OutputWriter(OutputStream outputStream) {
writer = new PrintWriter(new BufferedWriter(new OutputStreamWriter(outputStream)));
}
public OutputWriter(Writer writer) {
this.writer = new PrintWriter(writer);
}
public void close() {
writer.close();
}
public void println(long i) {
writer.println(i);
}
}
static class Utils {
public static int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
public static int[][] getComb(int sz, int mod) {
int[][] comb = new int[sz][sz];
for (int i = 0; i < sz; i++) {
comb[i][0] = 1;
for (int j = 1; j <= i; j++) {
comb[i][j] = comb[i - 1][j] + comb[i - 1][j - 1];
if (comb[i][j] >= mod) comb[i][j] -= mod;
}
}
return comb;
}
}
static class InputReader {
private InputStream stream;
private byte[] buf = new byte[1024];
private int curChar;
private int numChars;
public InputReader(InputStream stream) {
this.stream = stream;
}
public int read() {
if (this.numChars == -1) {
throw new InputMismatchException();
} else {
if (this.curChar >= this.numChars) {
this.curChar = 0;
try {
this.numChars = this.stream.read(this.buf);
} catch (IOException var2) {
throw new InputMismatchException();
}
if (this.numChars <= 0) {
return -1;
}
}
return this.buf[this.curChar++];
}
}
public int nextInt() {
int c;
for (c = this.read(); isSpaceChar(c); c = this.read()) {
;
}
byte sgn = 1;
if (c == 45) {
sgn = -1;
c = this.read();
}
int res = 0;
while (c >= 48 && c <= 57) {
res *= 10;
res += c - 48;
c = this.read();
if (isSpaceChar(c)) {
return res * sgn;
}
}
throw new InputMismatchException();
}
public String next() {
int c;
while (isSpaceChar(c = this.read())) {
;
}
StringBuilder result = new StringBuilder();
result.appendCodePoint(c);
while (!isSpaceChar(c = this.read())) {
result.appendCodePoint(c);
}
return result.toString();
}
public static boolean isSpaceChar(int c) {
return c == 32 || c == 10 || c == 13 || c == 9 || c == -1;
}
}
static class SCCTarjan {
List<Integer>[] graph;
boolean[] visited;
Stack<Integer> stack;
int time;
int[] lowlink;
List<List<Integer>> components;
public List<List<Integer>> scc(List<Integer>[] graph) {
int n = graph.length;
this.graph = graph;
visited = new boolean[n];
stack = new Stack<>();
time = 0;
lowlink = new int[n];
components = new ArrayList<>();
for (int u = 0; u < n; u++)
if (!visited[u])
dfs(u);
return components;
}
void dfs(int u) {
lowlink[u] = time++;
visited[u] = true;
stack.add(u);
boolean isComponentRoot = true;
for (int v : graph[u]) {
if (!visited[v])
dfs(v);
if (lowlink[u] > lowlink[v]) {
lowlink[u] = lowlink[v];
isComponentRoot = false;
}
}
if (isComponentRoot) {
List<Integer> component = new ArrayList<>();
while (true) {
int x = stack.pop();
component.add(x);
lowlink[x] = Integer.MAX_VALUE;
if (x == u)
break;
}
components.add(component);
}
}
}
}
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
const int maxn = 5005;
const int maxelem = 2000006;
const int MOD = 1000000007;
char gr[maxn][maxn];
string init[maxn];
int mincnt[maxn], maxcnt[maxn];
int c[maxn][maxn];
int n, m, A, B;
bool was[maxn];
vector<int> order;
vector<bool> can[maxn];
bool nowcan[maxelem];
char s[maxelem];
int gcd[maxn];
vector<int> comp[maxn];
void preorder(int cur)
{
if (was[cur]) return;
was[cur] = true;
for (int i = 0; i < n; i++) if (gr[cur][i] == '1') preorder(i);
order.pb(cur);
}
void color(int cur, int cc)
{
if (was[cur]) return;
was[cur] = true;
gcd[cc] = __gcd(gcd[cc], (int)init[cur].size());
comp[cc].pb(cur);
for (int i = 0; i < n; i++) if (gr[i][cur] == '1') color(i, cc);
}
int getc(int n, int k)
{
if (k < 0 || k > n) return 0;
return c[n][k];
}
int main()
{
scanf("%d%d%d", &n, &A, &B);
for (int i = 0; i < n; i++)
{
scanf("%s", gr[i]);
}
for (int i = 0; i < n; i++)
{
scanf("%*d");
scanf("%s", s);
init[i] = string(s);
for (int j = 0; j < (int)init[i].size(); j++) mincnt[i] += init[i][j] == '1';
maxcnt[i] = mincnt[i];
}
for (int i = 0; i < n; i++) if (!was[i]) preorder(i);
memset(was, 0, sizeof(was));
int cc = 0;
reverse(all(order));
for (auto t : order) if (!was[t])
{
color(t, cc);
cc++;
}
for (int i = 0; i < cc; i++)
{
can[i].resize(gcd[i]);
for (int j = 0; j < gcd[i]; j++) can[i][j] = false;
for (auto t : comp[i])
{
for (int j = 0; j < (int)init[t].size(); j++) if (init[t][j] == '1') can[i][j % gcd[i]] = true;
}
}
for (int i = 0; i < cc - 1; i++)
{
int g = __gcd(gcd[i], gcd[i + 1]);
for (int j = 0; j < g; j++) nowcan[j] = false;
for (int j = 0; j < gcd[i]; j++) nowcan[j % g] |= can[i][j];
for (int j = 0; j < gcd[i + 1]; j++) can[i + 1][j] = (can[i + 1][j] | nowcan[j % g]);
}
for (int i = 0; i < cc; i++)
{
for (auto t : comp[i])
{
for (int j = 0; j < (int)init[t].size(); j++) if (init[t][j] == '0' && can[i][j % gcd[i]]) maxcnt[t]++;
}
}
c[0][0] = 1;
for (int i = 1; i <= n; i++)
{
c[i][0] = 1;
for (int j = 1; j <= i; j++) c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % MOD;
}
int answer = 0;
for (int i = 0; i < n; i++)
{
int cntbigger = 0;
int cntupper = 0;
for (int j = 0; j < n; j++) if (i != j)
{
if (mincnt[j] > maxcnt[i]) cntbigger++;
else if (maxcnt[j] > maxcnt[i] || (maxcnt[j] == maxcnt[i] && j > i)) cntupper++;
}
if (cntbigger >= A) continue;
for (int j = max(0, B - 1 - cntbigger); j <= cntupper && j + cntbigger + 1 <= A && j + 1 <= B; j++)
{
answer = (answer + (ll)getc(cntupper, j) * getc(cntbigger, B - 1 - j)) % MOD;
}
}
cout << answer << endl;
return 0;
}
#include <bits/stdc++.h>
#define xx first
#define yy second
#define mp make_pair
#define pb push_back
#define fill( x, y ) memset( x, y, sizeof x )
#define copy( x, y ) memcpy( x, y, sizeof x )
using namespace std;
typedef long long LL;
typedef pair < int, int > pa;
inline int read()
{
int sc = 0, f = 1; char ch = getchar();
while( ch < '0' || ch > '9' ) { if( ch == '-' ) f = -1; ch = getchar(); }
while( ch >= '0' && ch <= '9' ) sc = sc * 10 + ch - '0', ch = getchar();
return sc * f;
}
const int MAXN = 5005;
const int MAXM = 2000005;
const int mod = 1e9 + 7;
int n, a, b, len[MAXN], can[MAXM], id_cnt, L[MAXN], R[MAXN], C[MAXN][MAXN];
int dfn[MAXN], scc[MAXN], low[MAXN], tim, num, st[MAXN], top, w[MAXN], ans;
vector < int > G[MAXN], id[MAXN], scc_bit[MAXN], v[MAXN];
char ch[MAXM];
inline void inc(int &x, int y) { x += y; if( x >= mod ) x -= mod; }
inline void dfs(int x)
{
dfn[ x ] = low[ x ] = ++tim; st[ ++top ] = x;
for( auto y : G[ x ] )
if( !dfn[ y ] ) dfs( y ), low[ x ] = min( low[ x ], low[ y ] );
else if( !scc[ y ] ) low[ x ] = min( low[ x ], dfn[ y ] );
if( dfn[ x ] == low[ x ] )
{
num++; int t = 0;
while( t ^ x )
{
scc[ t = st[ top-- ] ] = num;
w[ num ] = __gcd( w[ num ], len[ t ] );
v[ num ].pb( t );
}
scc_bit[ num ].resize( w[ num ] );
for( auto y : v[ num ] )
for( int d = 0 ; d < len[ y ] ; d++ ) if( can[ id[ y ][ d ] ] ) scc_bit[ num ][ d % w[ num ] ] = 1;
}
}
int main()
{
#ifdef wxh010910
freopen( "data.in", "r", stdin );
#endif
n = read(), a = read(), b = read();
for( int i = 0 ; i <= n ; i++ )
{
C[ i ][ 0 ] = 1;
for( int j = 1 ; j <= i ; j++ ) inc( C[ i ][ j ] = C[ i - 1 ][ j ], C[ i - 1 ][ j - 1 ] );
}
for( int i = 1 ; i <= n ; i++ )
{
scanf( "%s", ch + 1 );
for( int j = 1 ; j <= n ; j++ ) if( ch[ j ] == '1' ) G[ i ].pb( j );
}
for( int i = 1 ; i <= n ; i++ )
{
len[ i ] = read(); scanf( "%s", ch );
for( int j = 0 ; j < len[ i ] ; j++ ) id[ i ].pb( ++id_cnt ), can[ id_cnt ] = ch[ j ] == '1', L[ i ] += can[ id_cnt ];
}
for( int i = 1 ; i <= n ; i++ ) if( !dfn[ i ] ) dfs( i );
for( int i = num ; i > 1 ; i-- )
{
int g = __gcd( w[ i ], w[ i - 1 ] );
w[ i - 1 ] = g;
for( int j = 0 ; j < w[ i ] ; j++ ) scc_bit[ i - 1 ][ j % g ] |= scc_bit[ i ][ j ];
}
for( int i = 1 ; i <= n ; i++ )
{
int x = scc[ i ];
for( int j = 0 ; j < len[ i ] ; j++ )
R[ i ] += scc_bit[ x ][ j % w[ x ] ];
}
for( int i = 1 ; i <= n ; i++ )
{
int t1 = 0, t2 = 0;
for( int j = 1 ; j <= n ; j++ ) if( L[ j ] > R[ i ] ) t1++;
if( t1 >= a ) continue;
for( int j = 1 ; j <= n ; j++ ) if( L[ j ] <= R[ i ] && mp( R[ j ], j ) > mp( R[ i ], i ) ) t2++;
for( int j = 0 ; j < b && j <= t2 && j + t1 < a ; j++ )
inc( ans, 1LL * C[ t2 ][ j ] * C[ t1 ][ b - j - 1 ] % mod );
}
return printf( "%d\n", ans ), 0;
}






