Hi. I am trying to solve this problem.

For convenience, I have summarized the problem statement below (based on my understanding):

Given a directed graph with N vertices and E edges (with cycles and not necessarily connected), find the minimum number of edges that we need to retain such that connectivity between vertices is retained as given in the original graph.

For example, for the following graph:

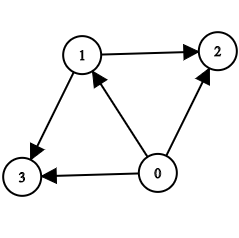
We should retain the edges:

0 -> 1
0 -> 3
1 -> 2
1 -> 3

So we must use a minimum of 4 edges.

Note that 0 -> 2 is redundant as