Hello, Codeforces!

I think many of you know about Mo's algorithm. For those, who don't know, please read this blog.

Here, I consider an alternative (and faster) approach of sorting queries in Mo's algorithm.

Table of contents

• Canonical version of the algorithm
• Achieving a better time complexity
  • Relation to TSP
  • Hilbert curve
• Benchmarks
• Applicability

Canonical version of the algorithm

The canonical version of this algorithm has 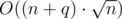time complexity if insertions and deletions work in O(1).

Usually, the two comparators for query sorting are used. The slowest one:

struct Query {
	int l, r, idx;
	
	inline pair<int, int> toPair() const {
		return make_pair(l / block, r);
	}
};

inline bool operator<(const Query &a, const Query &b) {
	return a.toPair() < b.toPair();
}

We know it can be optimized a little if for even blocks we use the reverse order for the right boundary:

struct Query {
	int l, r, idx;
	
	inline pair<int, int> toPair() const {
		return make_pair(l / block, ((l / block) & 1) ? -r : +r);
	}
};

inline bool operator<(const Query &a, const Query &b) {
	return a.toPair() < b.toPair();
}

Achieving a better time complexity

We can achieve 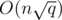complexity for Mo's algorithm (still assuming that insertions and deletions are O(1)). Note that 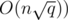is always better than 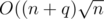. We can prove it as follows:

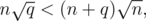
n²q < n(n + q)², 

nq < n² + 2nq + q², 

n² + nq + q² > 0

But how this complexity can be achieved?

Relation to TSP

At first, notice that changing the segment (l₁;r₁) to (l₂;r₂) will take |l₁ - l₂| + |r₁ - r₂| insertions and deletions.

Denote the queries as (l₁;r₁), (l₂;r₂), ..., (l_q;r_q). We need to permute them to minimize the number of operations, i. e. to find a permutation p₁, p₂, ... p_q such that total number of operations

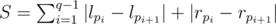
is minimal possible.

Now we can see the relationship between Mo's algorithm and TSP on Manhattan metrics. Boundaries of queries can be represented as points on 2D plane. And we need to find an optimal route to visit all these points (process all the queries).

But TSP is NP-complete, so it cannot help us to find the optimal query sorting order. Instead, we should use a fast heuristic approach. A good approach would be the use of recursive curves. Wikipedia says about using Sierpiński curve as a basis to find a good TSP solution.

But Sierpiński curve is not very convenient in implementation for integer point coordinates, so we will use another recursive curve: Hilbert curve.

Hilbert curve

Let's build a Hilbert curve on a 2^k × 2^k matrix and visit all the cells on the matrix according to this curve. Denote ord(i, j, k) as the number of cells visited before the cell (i, j) in order of Hilbert curve on the 2^k × 2^k matrix. The following picture shows ord(i, j) for each cell on the 8 × 8 matrix:

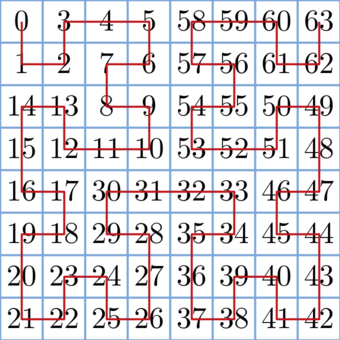
Now we can write a function to determine ord(i, j, k). It will do the following:

• Divide the matrix onto four parts (as Hilbert curve is built recursively, each part is a rotated Hilbert curve).
• Determine, in which of the four parts the cell (i, j) is located.
• Add all the cells in the previous parts. There are 4^n - 1·k or them, where k is the number of parts visited before the current one.
• Recursively go into the selected part (do not forget that it can be rotated).

The code looks in the following way:

inline int64_t hilbertOrder(int x, int y, int pow, int rotate) {
	if (pow == 0) {
		return 0;
	}
	int hpow = 1 << (pow-1);
	int seg = (x < hpow) ? (
		(y < hpow) ? 0 : 3
	) : (
		(y < hpow) ? 1 : 2
	);
	seg = (seg + rotate) & 3;
	const int rotateDelta[4] = {3, 0, 0, 1};
	int nx = x & (x ^ hpow), ny = y & (y ^ hpow);
	int nrot = (rotate + rotateDelta[seg]) & 3;
	int64_t subSquareSize = int64_t(1) << (2*pow - 2);
	int64_t ans = seg * subSquareSize;
	int64_t add = hilbertOrder(nx, ny, pow-1, nrot);
	ans += (seg == 1 || seg == 2) ? add : (subSquareSize - add - 1);
	return ans;
}

Assume the matrix has size 2^k × 2^k, where 2^k ≤ n (you can take k = 20 for most cases or find minimal such k that 2^k ≤ n). Now denote o_i as ord(l_i, r_i, k) on this matrix. Then sort the queries according to their o_i.

Here is the proof why this works in 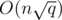time. Suppose we have n = 2^k and q = 4^l, where k and l are some integers. (If n and q are not powers of 2 and 4 respectively, we increase them, it don't have any effect on asymptotic). Now divide the matrix onto squares with size 2^l × 2^l. To travel between a pair of adjacent squares, we need 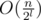time, so we can travel between all the squares in 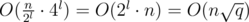time. Now consider the groups of queries inside a 2^l × 2^l square. Here we can travel from one query to another in 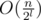, so we process all such groups of queries in 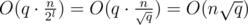. So the total time to process all the queries is 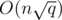, which was to be proved.

Benchmarks

Let's compare the canonical version of Mo's algorithm and the version with Hilbert order. To do this, we will use the problem 617E - XOR и любимое число with different constraints for n and q. The implementations are here:

• Standard implementation: code
• Mo with Hilbert curves: code

To reduce the amount of input and output, the generators are built into the code and the output is hashed.

For benchmarks I used Polygon. The results are here:

n	q		Standard Mo time	Mo+Hilbert time	Time ratio
400000	400000	1	2730 ms	2698 ms	1.012
1000000	1000000	1	13602 ms	10841 ms	1.255
500000	250000	2	3369 ms	2730 ms	1.234
1000000	500000	2	10077 ms	7644 ms	1.318
600000	200000	3	4134 ms	2901 ms	1.425
1000000	333333	3	8767 ms	6240 ms	1.405
600000	150000	4	4851 ms	2496 ms	1.944
1000000	250000	4	8672 ms	5553 ms	1.561
700000	140000	5	6255 ms	2854 ms	2.192
1000000	200000	5	8423 ms	5100 ms	1.652
750000	100000	7.5	5116 ms	2667 ms	1.918
1000000	333333	7.5	7924 ms	4009 ms	1.976
1000000	100000	10	7425 ms	3977 ms	1.866
1000000	40000	25	9671 ms	2355 ms	4.107
1000000	20000	50	9016 ms	1590 ms	5.670
1000000	10000	100	6879 ms	1185 ms	5.805
1000000	5000	200	5802 ms	857 ms	6.770
1000000	2500	400	4897 ms	639 ms	7.664

What is interesting, when I ran these codes locally even on the test with n = q, Hilbert version worked about three times faster.

Applicability

As you can see, such sorting order doesn't make Mo's algorithm work slower, and when q is significantly less than n, it works much faster than the classical version. So it is ideal for problems with n = 10⁶ and q = 10⁴. For smaller q solutions with naive query processing can pass.

Thanks to everyone who read this article! I hope it will be useful for someone.