| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
Help needed in a uva geometry problem
This a problem from UAP NCPC 2016. link: problem uva-13084
In short the description is: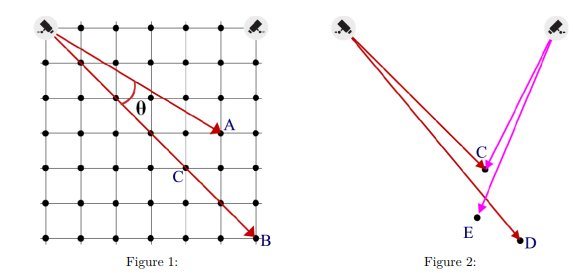 
A point in a n*n grid (n is maximum 5000) is considered troublesome if there exist another point in the grid which creates angle less than atan(1/k) and it is more than 0 degree where n^2<=k<=2n^2 with respect to the upper two corners. In the above picture C is a troublesome point. There are at most 10 test cases. No idea How to solve this problem. Any help?
| Rev. | Lang. | By | When | Δ | Comment | |
|---|---|---|---|---|---|---|
| en3 |
|
t.muttaqueen | 2018-10-03 08:17:21 | 47 | ||
| en2 |
|
t.muttaqueen | 2018-10-03 08:16:30 | 29 | Tiny change: 'atan(1/k) where n^2' -> 'atan(1/k) and it is more than 0 degree where n^2' | |
| en1 |
|
t.muttaqueen | 2018-10-03 08:12:19 | 643 | Initial revision (published) |
