In the name of God;
Hi, here I want to suggest some random functions for Testlib.
Testlib has nice random functions, here I want to suggest some other ones. The first and the second random functions are available in testlib, but the rest are not.
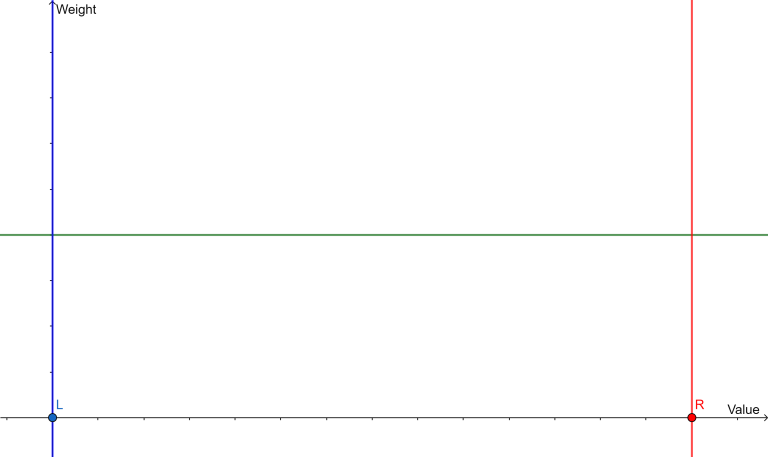
1, $$$\text{rnd.next(l, r)}$$$, it will return a random number in range $$$l$$$ to $$$r$$$ with equal weights :
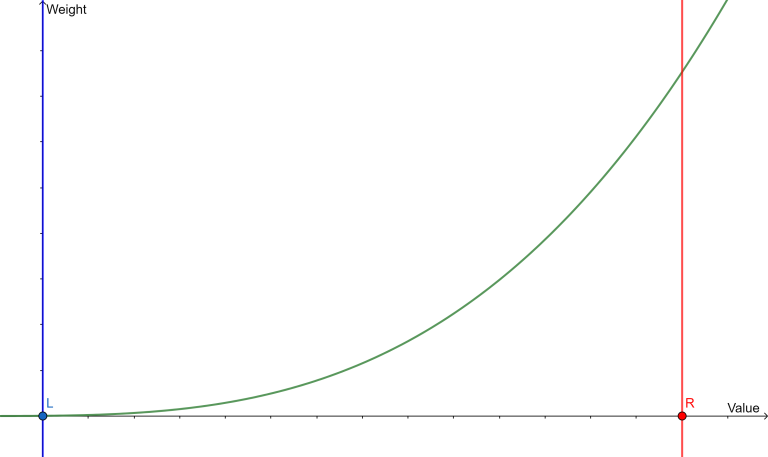
2, $$$\text{rnd.wnext(l, r, w)}$$$, it will return a random number in range $$$l$$$ to $$$r$$$ with monotonically increasing/decreasing weights depending on $$$w$$$ :
If $$$w = 0$$$ then it will be equal to $$$\text{rnd.next(l, r)}$$$.
If $$$w > 0$$$ :
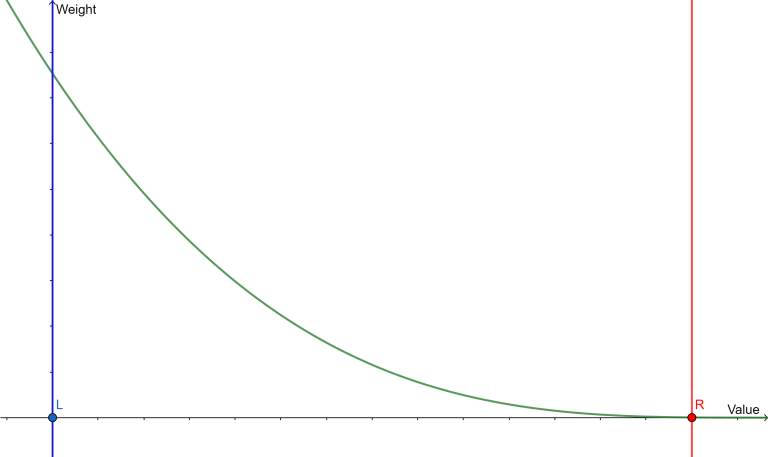
If $$$w < 0$$$ :
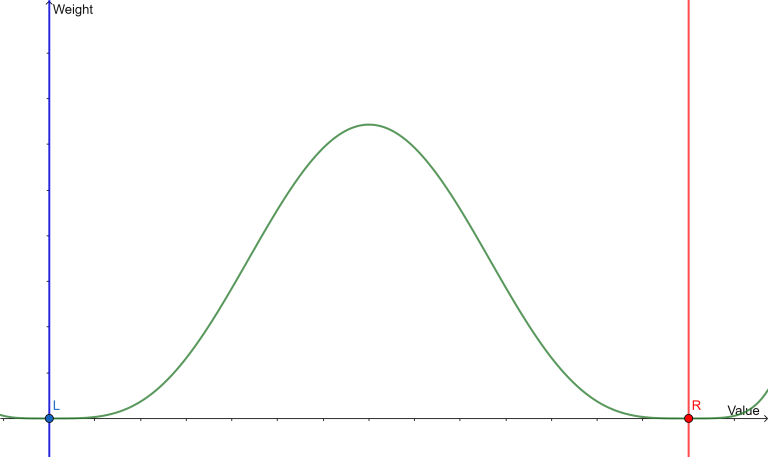
3, $$$\text{rnd.cnext(l, r, c)}$$$, it will return a random number in range $$$l$$$ to $$$r$$$ :
If $$$c = 0$$$ then it will be equal to $$$\text{rnd.next(l, r)}$$$
If $$$c > 0$$$ :
If $$$c < 0$$$, (I couldn't find a accurate graph for it) :
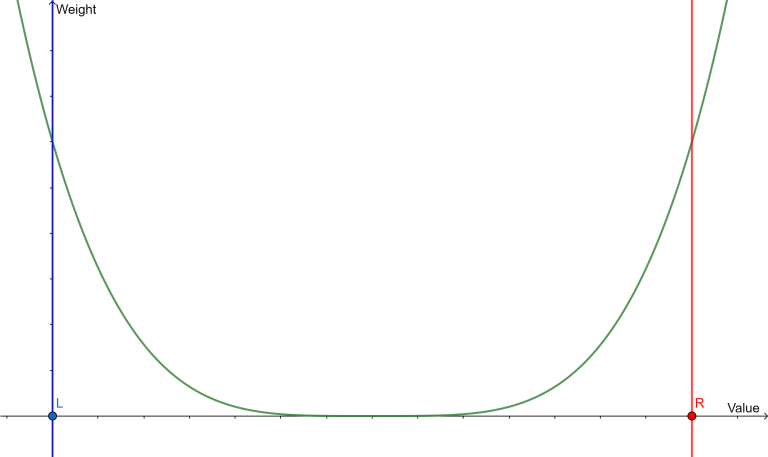
4, $$$\text{rnd.cnext(l, r, c1, c2)}$$$, it will return a random number in range $$$l$$$ to $$$r$$$ like $$$\text{rnd.cnext(l, r, c)}$$$, but its not centered around $$$\frac {r+l} 2$$$ : ($$$c1 \ge 0$$$ and $$$c2 \ge 0$$$)
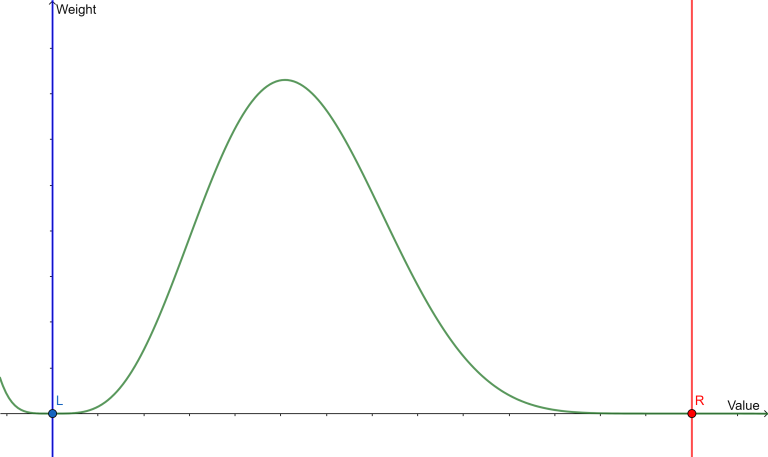
About the implementation of $$$\text{cnext(l, r, c1, c2)}$$$, its as follow :
Choose $$$c1+c2+1$$$ random numbers in rage $$$l$$$ to $$$r$$$ and sort them.
Print $$$c1+1$$$-th one.
As you can see if $$$c1 = c2$$$ then its equal to $$$\text{cnext(l, r, c1)}$$$.
If $$$c1 = 0$$$ then it will be equal to $$$\text{wnext(l, r, -c2)}$$$, if $$$c2 = 0$$$ then it will be equal to $$$\text{wnext(l, r, c1)}$$$.
You want to say that they are useless? Indeed they are very useful, open your eyes and find some examples! Please share them in the comment section.






