Bridge Tree(2-edge connected) decomposition of graph[Tutorial and Problems]

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	166
2	maomao90	163
2	Um_nik	163
4	atcoder_official	161
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	nor	153
9	Dominater069	153

Hello, codeforces!

I don't know how helpful will this be to anyone, but I thought it would be nice to share it. Before reading this blog, you should be familiar with the concept of Bridges in a graph.

What it can do

Find minimum number of edges to add in a graph, so that there are no bridges.
Add a single edge to minimize the number of bridges in a graph.
Given a graph, and queries in from A B C D: For the current query add an edge between nodes numbered A and B(note that this operation is temporary and only for the current query). Now, output the maximum number of bridge edges occuring on any path between C and D.

What is Bridge Tree of a graph?

One of the formal terms often used to describe Bridge tree is decomposing graph into 2-edge connected components and making a tree of it.

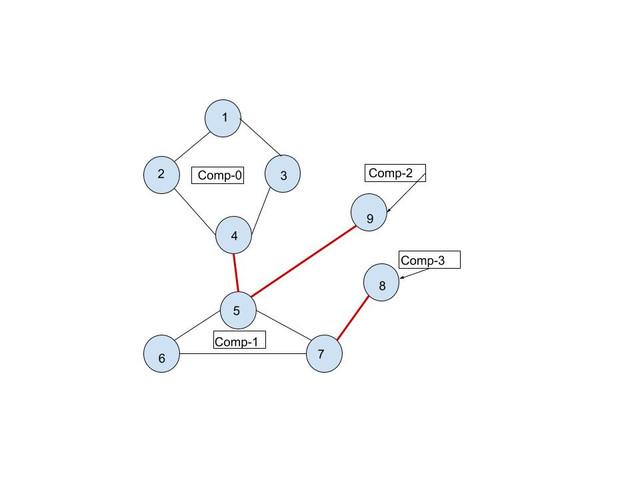
2-edge connected component in simple terms is a set of vertices grouped together into a component, such that if we remove any edge from that component, that component still remains connected. In short, it's a component which doesn't have any bridges in it.

So, how can we make bridge tree of a graph?

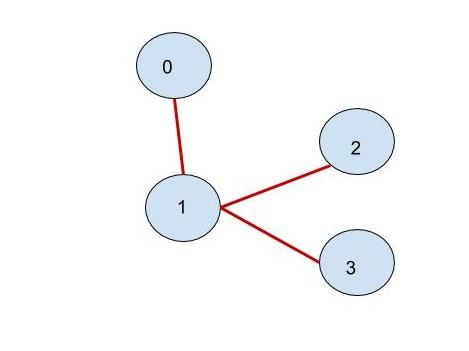
In Bridge Tree we will have => Nodes as:-> 2-edge connected components. and, edges as:-> Bridge connecting two different components.

Example, Consider we have a graph. (Red line edge is a bridge)

It's Bridge Tree would be,

How to implement

Find bridges in the graph and mark them.

Code

void dfs(int v, int p) {
    tin[v] = minAncestor[v] = ++timer;
    used[v] = 1;
    for(auto &e: g[v]) {
        int to, id;
        tie(to, id) = e;
        if(to == p) continue;
        if(used[to]) {
            minAncestor[v] = min(minAncestor[v], tin[to]);
        } else {
            dfs(to, v);
            minAncestor[v] = min(minAncestor[v], minAncestor[to]);
            if(minAncestor[to] > tin[v]) {
                isBridge[id] = true;
            }
        }
    }
}

Remove the bridge from the graph.
Run dfs/dsu or bfs whichever way you prefer to group one components and give vertices the component id in which they belong. (Note: Remove bridge means: while traversing make sure not to cross the bridge, so we can group vertices of one component)

Code

void dfs1(int v, int p) {
    used[v] = 1;
    comp[v] = compid;
    for(auto &e: g[v]) {
        int to, id;
        tie(to, id) = e;
        
        if(isBridge[id]) { // avoid traversing from this edge. so we get full component.
            continue;
        }
        if(used[to]) {
            continue;
        }
        dfs1(to, v);
    }
}

Traverse every edge, if it is a bridge, connect the two components via an edge.

Code

for(int i = 1; i <= M; ++i) {
    if(isBridge[i]) {
         int u, v;
         tie(u, v) = edges[i];
         // connect two componets using edge.
         tree[comp[u]].push_back(comp[v]);
         tree[comp[v]].push_back(comp[u]);
    }
}

Alternative Implementation:

There is also alternative implementation using dfs and queues(bfs) mentioned in this blog which is also on this same topic. Link

Honestly, i think using just dfs to find components is intuitively to me and easy to code. You can use any approach you like.

Full Code:

Code Link

Code

const int MAXN = 1e5 + 5;
const int MAXM = 1e5 + 5;

int N, M, timer, compid;

vector<pair<int, int>> g[MAXN];
bool used[MAXN], isBridge[MAXM];
int comp[MAXN], tin[MAXN], minAncestor[MAXN];

vector<int> tree[MAXN]; // Store 2-edge-connected component tree.(Bridge tree).

void dfs(int v, int p) {
    tin[v] = minAncestor[v] = ++timer;
    used[v] = 1;
    for(auto &e: g[v]) {
        int to, id;
        tie(to, id) = e;
        if(to == p) continue;
        if(used[to]) {
            minAncestor[v] = min(minAncestor[v], tin[to]);
        } else {
            dfs(to, v);
            minAncestor[v] = min(minAncestor[v], minAncestor[to]);
            if(minAncestor[to] > tin[v]) {
                isBridge[id] = true;
            }
        }
    }
}

void dfs1(int v, int p) {
    used[v] = 1;
    comp[v] = compid;
    for(auto &e: g[v]) {
        int to, id;
        tie(to, id) = e;
        
        if(isBridge[id]) { // avoid traversing from this edge. so we get full component.
            continue;
        }
        if(used[to]) {
            continue;
        }
        dfs1(to, v);
    }
}

vector<pair<int, int>> edges;

void addEdge(int from, int to, int id) {
    g[from].push_back({to, id});
    g[to].push_back({from, id});
    edges[id] = {from, to};
}

void initB() {

    for(int i = 0; i <= compid; ++i)
        tree[i].clear();
    for(int i = 1; i <= N; ++i)
        used[i] = false;
    for(int i = 1; i <= M; ++i)
        isBridge[i] = false;
    
    timer = 0;
    compid = 0;
}

void bridge_tree() {

    initB();
    
    dfs(1, -1); //Assuming graph is connected.
    
    for(int i = 1; i <= N; ++i)
        used[i] = 0;

    for(int i = 1; i <= N; ++i) {
        if(!used[i]) {
            dfs1(i, -1);
            ++compid;
        }
    }

    for(int i = 1; i <= M; ++i) {
        if(isBridge[i]) {
            int u, v;
            tie(u, v) = edges[i];
            // connect two componets using edge.
            tree[comp[u]].push_back(comp[v]);
            tree[comp[v]].push_back(comp[u]);
        }
    }
}

void init() {
    edges.clear(); edges.resize(M + 1);
    for(int i = 1; i <= N; ++i)
        g[i].clear();
}

void solve() {
    cin >> N >> M;

    init();

    for(int i = 1; i <= M; ++i) {
        int u, v;
        cin >> u >> v; addEdge(u, v, i);
    }

    bridge_tree();

}

Thanks to

I already found this blog about Bridge tree on quora(Link) but I found implementation hard to interpret. Also, thanks to Algorithms Live Channel on Youtube which really helped me to clear concepts on Bridge Finding and forming 2 edge connected component tree of a graph and biconnected components in general.

Problems

If you have any doubts regarding explanation, you can ask in comments. Also, if you have solved problems related to it, please share it here, I will update the Problems section.

Have a great day!

What it can do

What is Bridge Tree of a graph?

So, how can we make bridge tree of a graph?

How to implement

Alternative Implementation:

Full Code:

Thanks to

Problems

История