Решим следующую задачу:

Дана таблица $$$n \cdot m$$$, поступают 2 вида запросов в онлайне:

1) Прибавить $$$x$$$ на прямоугольнике $$$[l1, r1], [l2, r2]$$$, помимо ассоциативности операция должна быть коммутативна, например присваивание не подойдёт.

2) Посчитать сумму (минимум, ...) на прямоугольнике $$$[l1, r1], [l2, r2]$$$.

Сначала разберём, как делать прибавление на отрезке и сумму на отрезке без пушей в одномерном ДО.

В каждой вершине будем хранить $$$sum[v]$$$ и $$$add[v]$$$ — сумму на отрезке и сколько мы прибавим каждому элементу на отрезке. Рассмотрим запрос прибавления: для всех вершин, посещенных нашей функцией (на картинке желтые и зелёные), мы корректно пересчитаем значение в вершине, для суммы это $$$sum[v] += (min(r, rx)-max(l, lx)) \cdot x$$$, но сумма в вершинах ниже останется старой (красные). Чтобы это учесть в тех вершинах, в которых остановилась функция (зелёные) сделаем $$$add[v] += x$$$.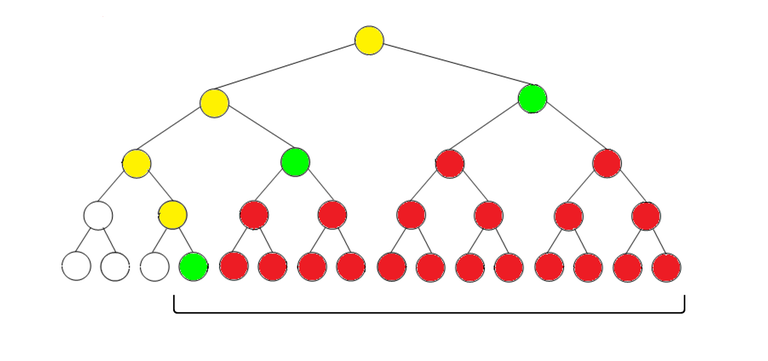

Номер корня равен 0, реализация на полуинтервалах

void upd(int l, int r, int lx, int rx, int v, int x) {
    if (l >= rx || r <= lx) return;
    sum[v] += (min(r, rx)-max(l, lx)) * x;

    if (l >= lx && r <= rx) {
        add[v] += x;
        return;
    }
    int m = (l + r) / 2;
    upd(l, m, lx, rx, v*2+1, x);
    upd(m, r, lx, rx, v*2+2, x);
}

Теперь запрос суммы. Чтобы узнать актуальную сумму в вершине, нужно взять сумму $$$add[p]$$$ по всем предкам, умноженную на длину отрезка, и sum[v]. Чтобы лучше понять, почему это так, попробуйте посчитать сумму для красной вершины на каринке. Функция запроса будет такой же, как и в обычном ДО, только нужно поддерживать сумму на пути от корня до вершины.

int ask(int l, int r, int lx, int rx, int v, int path) {
    if (l >= rx || r <= lx) return 0;
    if (l >= lx && r <= rx) {
        return sum[v] + (r-l) * path;
    }
    int m = (l + r) / 2;
    path += add[v];
    return ask(l, m, lx, rx, v*2+1, path) + ask(m, r, lx, rx, v*2+2, path);
}

Сделаем ДО по первой координате, в каждой вершине которого будет ДО на сумму, отвечающее за прямоугольник [l, r] [0, m]