Hi, recently I've been trying to do problems that are way too hard for me and stumbled across the following problem from Deltix Summer 2021: [https://mirror.codeforces.com/contest/1556/problem/E](https://mirror.codeforces.com/contest/1556/problem/E). I would recommend people actually go and try the solve the problem first before looking at this post as there will be problem spoilers here. ↵
↵
I took the day trying to think of solutions to this problem and I actually made a handful of nice observations but ultimately got stuck at some point and didn't really figure out what to do. After a lot of frustration I eventually decided to look at the editorial, but even after viewing the solution I was still stumped about the intuition behind the answer. I looked on youtube as well and didn't find much of use which led me to some sort of upset state about not being able to understand the problem well. ↵
↵
Regardless I kept thinking throughout the day and recently the problem solution has hit me in a very elegant manner that I'd like to share with you. I'll start from my original thinking about the problem. The problem statement basically summed up to how we should fix some subarray so that the elements of a and b are the same while using operations that alternate between incrementing a and incrementing b. I wrote out the sample case and it became apparent pretty quickly that the actual solution would only depend on what the difference between a_i and b_i would be. I made note of storing some difference array dif and continued on. ↵
↵
After some fumbling around and realizing I read the criteria of the operations wrong I stepped back and thought of the problem as one where we should be choosing the closest positive value for each negative value. The greedy method made me think a bit about bracket sequences as I noticed a lot of similarities between those types of problems and the one I was currently facing. For example if the value of dif_1 was positive it would be impossible to deal with such a case because there would be no negative values to "balance" it. Likewise for a case where we had some negative value at the end there would be no way to deal with a case b balancing it out with positive values further down the segment. I began to write the problem as a regular bracket sequence where a negative number n would signify using n ( brackets and a positive value p would signify using p ) brackets. Of course I had no proof that such problems were even remotely similar but to my intuition this seemed like the most logical step to reduce the problem. In fact, the idea checked out, such a sequence was only possible if the bracket sequence was regular, else we would run into a case where no matter how many negative values were incremented before a ) we would never be able to balance out the ) and would run into a case where we had a ) at the beginning which would be impossible to remove. Likewise for ( if we did not have enough ) after it we would be forced into a bad position. Aha! Done with the problem onto another―― oh it's asking for the minimum amount of such operations... So I slumped down in my seat a little bit. ↵
↵
This seemed like a much more difficult problem, with some thinking I eventually came up with the idea to split our bracket sequence into pieces of similar types. For example: (((( | ))) | ( | )). With some further thinking I convinced myself that we should always take as many brackets as we could which becomes the number of such segments. My reasoning for this was basically that if we didn't we would have to do later, so we might as well do so now. So this left me with the following problem, how are we supposed to figure out for any subsegment the amount of times it would take for us to make such a subsegment empty while using this sort of method. ↵
↵
I was stuck here for a while, I thought we could maybe do this operation once for the original sequence and then use that as our best result for every subsegment but that seemed complicated and I didn't really see a clear way to deal with the fact that the whole array and each subsegment didn't really line up too well when trying to take this approach. There would be issues regarding how we could quickly find exactly which operation made this whole subsegment 0's and having values we removed have to update multiple possible queries. It just didn't make sense to me. After a lot more diagrams (one in which I accidentally found something very useful but never bothered to think about it) I eventually gave up and turned to the editorial, a bit disappointed that I was stuck on this one step. The editorial gave me the solution and a proof, but this left me still unsatisfied, I didn't think I could simply solve this by just guessing the solution and I wanted a way to intuitively find it. I also looked in the comments and on youtube but I didn't totally understand how people were coming up with the solution and I still wanted to find if the things I was doing before could translate nicely into a solution. ↵
↵
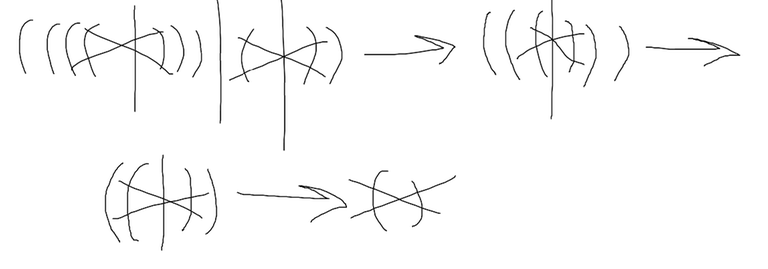
I eventually relaxed a bit and came back to the problem, hoping to simplify things. As I put my pencil down onto the paper and drew out a RBS it suddenly occurred to me that I had done something before which might be very useful. When I was simulating my approach I was doing the following: ↵
↵
↵
↵
The thing I was doing was essentially crossing out very close brackets that were of the form () to make my life easier when writing down the simulation on paper. Only now did it occur to me that such a way of representing operations was actually incredibly useful as it allowed for the following:↵
↵
↵
↵
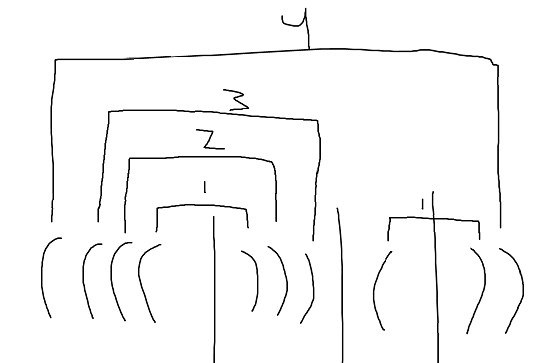
Essentially what I had constructed before by just writing stuff nicely on paper was actually a direct representation of the depths of a bracket sequence where the maximum depth was the amount of operations I needed. I was excited by such a nice way of representing the problem and quickly proved myself correct. It turned out that something very hard could be simplified into a much easier problem through just some concepts I had used before and a little bit of luck. It also made me have a deeper appreciation for such problems which, if worked out completely, actually are very instructive. ↵
↵
That's really all I have to say for this story, not sure why I posted it but I guess I just felt like I had to share my excitement a bit~
↵
I took the day trying to think of solutions to this problem and I actually made a handful of nice observations but ultimately got stuck at some point and didn't really figure out what to do. After a lot of frustration I eventually decided to look at the editorial, but even after viewing the solution I was still stumped about the intuition behind the answer. I looked on youtube as well and didn't find much of use which led me to some sort of upset state about not being able to understand the problem well.
↵
Regardless I kept thinking throughout the day and recently the problem solution has hit me in a very elegant manner that I'd like to share with you. I'll start from my original thinking about the problem. The problem statement basically summed up to how we should fix some subarray so that the elements of a and b are the same while using operations that alternate between incrementing a and incrementing b. I wrote out the sample case and it became apparent pretty quickly that the actual solution would only depend on what the difference between a_i and b_i would be. I made note of storing some difference array dif and continued on. ↵
↵
After some fumbling around and realizing I read the criteria of the operations wrong I stepped back and thought of the problem as one where we should be choosing the closest positive value for each negative value. The greedy method made me think a bit about bracket sequences as I noticed a lot of similarities between those types of problems and the one I was currently facing. For example if the value of dif_1 was positive it would be impossible to deal with such a case because there would be no negative values to "balance" it. Likewise for a case where we had some negative value at the end there would be no way to deal with a case b balancing it out with positive values further down the segment. I began to write the problem as a regular bracket sequence where a negative number n would signify using n ( brackets and a positive value p would signify using p ) brackets. Of course I had no proof that such problems were even remotely similar but to my intuition this seemed like the most logical step to reduce the problem. In fact, the idea checked out, such a sequence was only possible if the bracket sequence was regular, else we would run into a case where no matter how many negative values were incremented before a ) we would never be able to balance out the ) and would run into a case where we had a ) at the beginning which would be impossible to remove. Likewise for ( if we did not have enough ) after it we would be forced into a bad position. Aha! Done with the problem onto another―― oh it's asking for the minimum amount of such operations... So I slumped down in my seat a little bit.
↵
This seemed like a much more difficult problem, with some thinking I eventually came up with the idea to split our bracket sequence into pieces of similar types. For example: (((( | ))) | ( | )). With some further thinking I convinced myself that we should always take as many brackets as we could which becomes the number of such segments. My reasoning for this was basically that if we didn't we would have to do later, so we might as well do so now. So this left me with the following problem, how are we supposed to figure out for any subsegment the amount of times it would take for us to make such a subsegment empty while using this sort of method.
↵
I was stuck here for a while, I thought we could maybe do this operation once for the original sequence and then use that as our best result for every subsegment but that seemed complicated and I didn't really see a clear way to deal with the fact that the whole array and each subsegment didn't really line up too well when trying to take this approach. There would be issues regarding how we could quickly find exactly which operation made this whole subsegment 0's and having values we removed have to update multiple possible queries. It just didn't make sense to me. After a lot more diagrams (one in which I accidentally found something very useful but never bothered to think about it) I eventually gave up and turned to the editorial, a bit disappointed that I was stuck on this one step. The editorial gave me the solution and a proof, but this left me still unsatisfied, I didn't think I could simply solve this by just guessing the solution and I wanted a way to intuitively find it. I also looked in the comments and on youtube but I didn't totally understand how people were coming up with the solution and I still wanted to find if the things I was doing before could translate nicely into a solution.
↵
I eventually relaxed a bit and came back to the problem, hoping to simplify things. As I put my pencil down onto the paper and drew out a RBS it suddenly occurred to me that I had done something before which might be very useful. When I was simulating my approach I was doing the following: ↵
↵
↵
↵
The thing I was doing was essentially crossing out very close brackets that were of the form () to make my life easier when writing down the simulation on paper. Only now did it occur to me that such a way of representing operations was actually incredibly useful as it allowed for the following:↵
↵
↵
↵
Essentially what I had constructed before by just writing stuff nicely on paper was actually a direct representation of the depths of a bracket sequence where the maximum depth was the amount of operations I needed. I was excited by such a nice way of representing the problem and quickly proved myself correct. It turned out that something very hard could be simplified into a much easier problem through just some concepts I had used before and a little bit of luck. It also made me have a deeper appreciation for such problems which, if worked out completely, actually are very instructive.
↵
That's really all I have to say for this story, not sure why I posted it but I guess I just felt like I had to share my excitement a bit~





