Всем спасибо за участие! Задачи следуют в порядке, в котором они шли на оригинальном соревновании.

562A - Логистические вопросы

(в трансляции: 566C - Логистические вопросы)

Формализуем задачу. Нам дано необычное определение расстояния по дереву: ρ(a, b) = dist(a, b)^1.5. У каждой вершины есть её вес w_i. Нужно как-то так выбрать место x для проведения соревнования, чтобы минимизировать сумму взвешенных расстояний от всех вершин до неё: f(x) = w₁ρ(1, x) + w₂ρ(x, 2) + ... + w_nρ(x, n).

Давайте изучим свойства функции f(x). Мысленно разрешим себе ставить точку x не только в вершины дерева, но и в любую точку на ребре, доопределив естественным образом расстояние от точки внутри ребра до всех остальных вершин (например, середина ребра длины 4 находится на обычном расстоянии 2 от концов ребра).

Утверждение 1. На любом пути 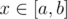в дереве функция ρ(i, x) является выпуклой вниз. Действительно, функция dist(i, x) на любом пути выглядит как график функции abs(x), то есть сначала линейно убывает до ближайшей к i точки на пути [a, b], а потом линейно возрастает. Взяв композицию с выпуклой возрастающей функциея t^1.5, как нетрудно видеть, мы снова получим выпуклую вниз на пути функцию. Здесь под функцией на пути мы подразумеваем обычную функцию действительной переменной x, где под x мы подразумеваем координату точки x на пути [a, b], или, что то же самое, dist(a, x). Таким образом, каждое из слагаемых в определении функции f(x) выпукло вниз на любом пути в дереве, а значит и функция f(x) выпукла на любом пути в дереве.

Будем называть функции, выпуклые вниз на любом пути в дереве выпуклыми на дереве. Сформулируем пару утверждений про выпуклые функции на дереве.

Утверждение 2. У выпуклой на дереве функции не может быть двух различных локальных минимумов. Действительно, в противном случае на пути между двумя этими минимумами функция сначала возрастает, а в конце убывает, что нарушает условие на выпуклость на этом пути.

Таким образом, у выпуклой вниз функции f(x) есть единственный локальный минимум на дереве, совпадающий с глобальным.

Утверждение 3. Из каждой вершины v дерева существует не более одного ребра, при движении по которому функция убывает. Действительно, в противном случае, если рассмотреть путь, образованный двумя такими рёбрами, то в точке, соответствующей вершине v, функция не будет выпукла вниз.

Назовём направление ребра из вершины v, при движении по которому убывает функция, градиентом функции f в точке x. Согласно утверждению 3, у выпуклой вниз функции f в любой вершине либо однозначно определён градиент, либо вершина является минимумом (глобальным).

Предположим, мы умеем некоторым образом эффективно искать направление градиента из вершины v. Научимся, пользуясь этим знанием и утверждениями 2 и 3 находить глобальный минимум. Если бы наше дерево представляло собой бамбук, то задача бы стала обычной одномерной задачей минимизации выпуклой функции, которая эффективно решается бинарным поиском, т. е. дихотомией. Нам же нужен некоторый эквивалент дихотомии на дереве. Что же это за эквивалент?

Воспользуемся centroid decmoposition! Действительно, возьмём центр дерева (т. е. такую вершину, что размеры всех её поддеревьев не превосходят n / 2). По утверждению 3 можно рассмотреть градиент функции в центре дерева. Во-первых, у функции может не оказаться градиента в центре дерева, что значит, что мы уже нашли оптимум. Иначе, мы знаем, что глобальный минимум расположен именно в поддереве в направлении градиента, значит все остальные поддеревья и сам центр можно выбросить из рассмотрения и оставить только выбранное поддерево. Таким образом, за один подсчёт градиента мы сократили в два раза количество вершин в рассматриваемой части дерева.

Значит, за подсчётов градиента мы практически научились решать задачу. Осталось только понять, где именно расположен ответ. Заметим, что глобальный оптимум, скорее всего, окажется внутри какого-то ребра. Тогда, как нетрудно видеть, оптимальной вершиной является один из концов этого ребра, а именно, одна из двух последних рассмотренных в процессе нашего алгоритма вершин. В какой именно можно определить, явно вычислив значение функции в них и взяв меньшее.

Теперь научимся считать направление градиента в вершине v. Зафиксируем одно поддерево u_i вершины v. Рассмотрим производную всех слагаемых, соответствующих поддереву u_i при движении в поддерево u_i, и обозначим её за der_i. Тогда, как нетрудно видеть, производная f(x) при движении от x = v в сторону поддерева u_i есть  - der₁ - der₂ - ... - der_i - 1 + der_i - der_i + 1 - ... - der_k, где k — степень вершины v. Таким образом, мы можем за один запуск обхода из вершины v определить все вершины der_i, а значит, и направление градиента, найдя с помощью формулы выше направление, в котором производная функции отрицательна.

Таким образом, получилось решение за .

562B - Клика в графе делителей

(в трансляции: 566F - Клика в графе делителей)

Упорядочим числа в искомой клике по возрастанию. Заметим, что чтобы множество X = {x₁, ..., x_k} образовывало клику, необходимо и достаточно, чтобы 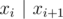для (1 ≤ i ≤ k - 1). Таким образом, нетрудно сформулировать задачу динамического программирования: D[x] есть длина наибольшей подходящей возрастающей подпоследовательности, заканчивающейся в числе x. Формула пересчёта: 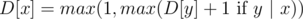по всем x, лежащим в A.

Если оформлять задачу динамического программирования в виде динамики "вперёд", то легко оценить сложность получившегося решения: в худшем случае количество переходов есть .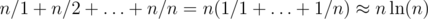

562C - Восстановление карты

(в трансляции: 566E - Восстановление карты)

Назовём окрестностью вершины — множество, состоящее из вершины и всех близких к ней вершин. Таким образом, нам известен набор окрестностей всех вершин в некотором произвольном порядке, причём каждая окрестность также перечислена в произвольном порядке.

Назовём вершину дерева внутренней, если она не является листом дерева. Аналогично, назовём ребро дерева внутренним, если оно соединяет две внутренних вершины. Заметим, что если две окрестности пересекаются ровно по двум элементам a и b, то a и b обязаны быть соединены ребром, причём ребро (a, b) является внутренним. Наоборот, любое внутреннее ребро (a, b) может быть найдено как пересечение каких-то двух окрестностей С и D двух вершин c и d, таких что в дереве есть путь c – a – b – d. Таким образом, мы можем найти все внутренние рёбра, рассмотрев попарные пересечения всех окрестностей. Это можно сделать за время порядка n³ / 2 наивно, либо в 32 раза быстрее, воспользовавшись битовым сжатием.

Заметим, что зная все внутренние рёбра, мы можем узнать все внутренние вершины, за исключением случая, когда граф представляет из себя звезду (т. е. вершину, к которой подцеплены все остальные). Случай звезды нужно разобрать отдельно.

Теперь мы знаем все листы, все внутренние вершины и структуру дерева на внутренних вершинах. Осталось только определить для каджого листа, к какой внутренней вершине он подцеплен. Это можно сделать следующим образом. Рассмотрим лист l. Рассмотрим все окрестности, его содержащие. Рассмотрим минимальную по включению окрестность — утверждается, что это есть окрестность L, соответствующая самому листу l. Рассмотрим все внутренние вершины в L. Их не может быть меньше двух. Если их три или более, то мы можем однозначно определить, к какой из них надо подцепить l — это должна быть та вершина из них, которая имеет степень внутри L больше единицы. Если же их ровно две (скажем, a и b), то определить, к кому из них надо подцепить l, несколько сложнее.

Утверждение: l должна быть подсоединена к той из двух вершин a и b, у которой степень по всем внутренним рёбрам — ровно один. Действительно, если бы l была подсоединена к вершине со внутренней степнью два или более, мы бы рассмотрели этот случай ранее.

Если же у обоих вершин a и b внутренняя степень — 1, то наш граф имеет вид гантели (ребро (a, b), и все остальные вершины, подцепленные либо за a, либо за b). Такой случай также придётся разобрать отдельно.

Разбор двух специальных случаев оставляется пытливому читателю как несложное упражнение.

562D - Реструктуризация компании

(в трансляции: 566D - Реструктуризация компании)

Эта задача допускает множество решений с разными асимптотиками. Опишем решение за .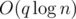

Рассмотрим сначала задачу, в которой присутствуют только запросы второго и третьего типа. Её можно решить следующим образом. Отметим всех работников в ряд на прямой от 1 до n. Заметим, что отделы представляют собой отрезки из подряд идущих работников. Будем поддерживать эти отрезки в любой логарифмической структуре данных, например в сбалансированном дереве поиска (std::set или TreeSet). Объединяя все отделы с позиции x по позицию y, вытаскиваем все отрезки, попавшие в диапазон [x, y] и сливаем их. Для ответа на запрос третьего типа проверяем, лежат ли работники x и y в одном отрезке. Таким образом, мы получаем решение более простой задачи за на запрос.

Добавляя запросы первого типа мы на самом деле разрешаем некоторым отрезкам на прямой относиться к одному и тому же отделу. Добавим в решение систему непересекающихся множеств, которая будет поддерживать классы эквивалентности на отрезках. Теперь запросы первого типа можно реализовать как вызов merge в системе непересекающихся множеств от номеров отделов, к которым принадлежат сотрудники x и y. Также в запросах второго типа надо не забывать вызывать merge от всех удаляемых отрезков.

Получилось решение за время .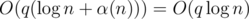

562E - Макс и Мин

(в трансляции: 566G - Макс и Мин)

Сформулируем задачу в геометрической интерпретации. У Макса и у Мина есть набор векторов из первой координатной четверти на плоскости и точка (x, y). За свой ход Макс может прибавить любой из имеющихся у него векторов к (x, y), а Мин — вычесть. Мин хочет добиться, чтобы точка (x, y) оказалась строго в третьей координатной четверти, Макс пытается ему помешать. Обозначим вектора Макса за Mx_i, вектора Мина за Mn_j.

Сформулируем очевидное достаточное условие для Макса, чтобы тот мог выиграть. Рассмотрим некоторое неотрицательное направление на плоскости, т. е. вектор (a, b), такой что a, b ≥ 0, при этом хотя бы одно из чисел a, b — не ноль. Тогда если среди ходов Макса есть такой вектор Mx_i, что он не короче всех векторов Мина Mn_j вдоль направления (a, b), то Макс может гарантировать себе победу. Здесь под длиной вектора v вдоль направления (a, b) подразумевается скалярное произведение вектора v на вектор (a, b).

Действительно, пусть Макс постоянно ходит в этот вектор Mx_i. Тогда за пару ходов Макса и Мина точка (x, y) сдвинется на вектор Mx_i - Mn_j для некоторого j, а значит её сдвиг вдоль вектора (a, b) составит ((Mx_i - Mn_j), (a, b)) = (Mx_i, (a, b)) - (Mn_j, (a, b)) ≥ 0. Значит, так как исходно скалярное произведение ((x, y), (a, b)) = ax + by > 0, то и в любой момент времени ax + by будет строго положительно. А значит, Мин ни в какой момент времени не сможет добиться чтобы x и y стали оба отрицательными (так как это значило бы, что ax + by < 0).

Теперь сформулируем некоторый вариант обратного утверждения. Пусть вектор Макса Mx_i лежит строго внутри треугольника, образованного векторами Мина Mn_j и Mn_k. При этом, вектор Mx_i не может лежать на отрезке [Mn_j, Mn_k], но может быть коллинеарен одному из векторов Mn_j и Mn_k.

Заметим, что раз Mx_i лежит строго внутри треугольника, натянутого на Mn_j и Mn_k, то его можно продлить до вектора Mx'_i, конец которого лежит на отрезке [Mn_j, Mn_k]. В силу линейной зависимости Mx'_i и Mn_j, Mn_k, имеем, что Mx'_i = (p / r)Mn_j + (q / r)Mn_k, где p + q = r и p, q, r — целые неотрицательные числа. Это эквивалентно rMx'_i = pMn_j + qMn_k, а значит, если на каждые r ходов Макса в Mx_i мы будем отвечать p ходами Мина в Mn_j и q ходами Мина в Mn_k, то суммарный сдвиг составит  - pMn_j - qMn_k + rMx_i =  - rMx'_i + rMx_i =  - r(Mx'_i - Mx_i), то есть вектор со строго отрицательными компонентами. Таким образом, мы можем мажорировать данный ход Макса, т. е. он ему невыгоден.

Естественным образом возникает желание построить выпуклую оболочку на ходах Мина и посмотреть на все ходы Макса относительно неё. Если ход Макса лежит внутри выпуклой оболочки ходов Мина, то из предыдущего утверждения этот ход Максу невыгоден. В противном случае, возможно два варианта.

Либо этот ход пересекает выпуклую оболочку, но выходит из неё наружу — в таком случае этот ход Макса не короче всех ходов Мина в некотором неотрицательном направлении, а значит Макс победил.

Либо же, вектор Макса находится сбоку от выпуклой оболочки ходов Мина. Пусть для определённости вектор Mx_i В таком случае, требуется отдельный анализ. Рассмотрим самый верхний из векторов Мина. Если вектор Mx_i не ниже самого верхнего из ходов Макса Mx_j, то по первому утверждению Макс может выиграть, ходя исключительно в этот вектор. В противном же случае, как несложно видеть, разность Mn_i - Mx_j — это вектор со строго отрицательными компонентами, ходя в который мы можем мажорировать соответствующий вектор Макса.

Значит, полная версия критерия победы Мина выглядит следующим образом. Рассмотрим выпуклую оболочку ходов Мина и продлим её от самой верхней точки влево и от самой правой точки вниз. Если все ходы Макса попадают строго внутрь образованной фигуры, то Мин побеждает. Иначе побеждает Макс.

562F - Подбор имён

(в трансляции: 566A - Подбор имён)

Сформиурем бор из всех имён и псевдонимов. Отметим красным все вершины, соответствующие именам, и синим все вершины, соответствующие всем псевдонимам (одна вершина может быть отмечена несколько раз, в том числе разными цветами). Заметим, что если мы сопоставили имя a и псевдоним b, то качество такого сопоставления может быть выражено как lcp(a, b) = 1 / 2(2 * lcp(a, b)) = 1 / 2(|a| + |b| - (|a| - lcp(a, b)) - (|b| - lcp(a, b))), что представляет собой константу 1 / 2(|a| + |b|), из которой вычитается половина длины пути между a и b по бору. Таким образом, мы должны соединить все красные вершины с синими, минимизировав суммарную длину путей.

Нетрудно видеть, что такая задача решается жадным образом следующей рекурсивной процедурой: если у нас есть вершина v, в поддереве которой x красных вершин и y синих вершин, то мы должны сопоставить min(x, y) красных вершин этого поддерева синим вершинам, а оставшиеся max(x, y) - min(x, y) красных или синих вершин "отдать" на уровень выше. Корректность данного алгоритма легко объясняется следующим соображением. Ориентируем ребро каждого пути по направлению от красной вершины к синей. Если ребро получает две разных ориентации, то два пути, на которых оно лежит, легко "развести", уменьшив их суммарную длину.

Таким образом, получается несложное решение за O(sumlen), где sumlen — суммарная длина всех имён и псевдонимов.

562G - Репликация процессов

(в трансляции: 566B - Репликация процессов)

Эту задачу можно решить симулируя процесс реплицирования. Будем к каждому шагу поддерживать список всех репликаций, которые в текущий момент можно применить. Применяем любую репликацию, после чего обновляем список, добавляя/удаляя все подходящие или переставшие быть подходящими репликации со всех затронутых на данном шаге серверов. Список репликаций можно поддерживать в структуре данных "двусвязный список", которая позволяет за O(1) добавлять и удалять элемент в/из множества и вынимаь произвольный элемент множества.

Доказательство корректности этого алгоритма несложно и оставляется как упражнение (впрочем, если будет большое количество желающих, оно появится здесь позднее).

Получается решение за O(n) операций (впрочем, константа, скрытая за O-нотацией весьма немаленькая — один только ввод составляет 12n чисел, да и само решение оперирует по меньшей мере константой 36).

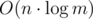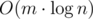Мы были вынуждены удалить регистрации, сделанные до 00:00, так как регистрационная форма на тот момент не поддерживала регистрацию команд. Пожалуйста, пройдите регистрацию вновь, если ваша регистрация была удалена.

Вчера завершился финал чемпионата VK Cup 2015, о котором вы могли прочитать в предыдущих наших постах. Осталось объявить последнее событие, связанное с прошедшим чемпионатом — онлайн-трансляцию, которая состоится в четверг 30 июля в 19:00 по Москве. К соревнованию допускаются как индивидуальные участники, так и команды из двух человек, которые желают почувствовать себя участниками финала соревнования. Трансляция продлится три часа, задачи будут перемешаны по сравнению с оригинальным порядком. Допускаются участники обоих дивизионом, но мы считаем своим долгом предупредить, что для участников из второго дивизиона набор задач, скорее всего, будет слишком сложным. Этот раунд является рейтинговым раундом Codeforces.

В заключение мы хотели бы поблагодарить всех людей, которые помогли чемпионату состояться. Придумывали и готовили задачи для вас сотрудники ВКонтакте, члены команды Codeforces и другие люди, любезно предложившие свою помощь: PavelKunyavskiy, burunduk3, Dmitry_Egorov, Kurpilyansky, dark_ai, MikeMirzayanov, Zlobober, MaximShipko, kuviman, Nickolas, Errichto, sankear и malcolm. Хочется сказать большое спасибо людям, прорешивавшим наши раунды, и дававшим ценные советы по поводу задач: winger и AlexFetisov. Также, мы благодарим всех работников ВКонтакте, с которыми вместе мы занимались проведением чемпионата: burunduk3, Burunduk2, KOTEHOK и многих других. Спасибо!

Всем удачи на онлайн-трансляции!

UPD: Обратите внимание, что во время раунда команде разрешается пользоваться только одним компьютером. Это значит, что программировать/пользоваться консолью/как-либо иначе продвигаться в решении задач в один момент времени можно только с одного компьютера. Единственное, что разрешается делать с двух компьютеров — это читать условия.

UPD2: Так как это командное соревнование, специально для вашего удобства мы выкладываем запароленный архив с pdf-условиями задач: vkcup2015-mirror-statements.zip. С началом тура мы опубликуем пароль к нему.

UPD3: В раунде будет использована динамическая разбалловка с шагом в 250 очков.

UPD4: По техническим причинам начало раунда переносится на 19:20 по Москве.

UPD5: Пароль на архив с условиями: vkcup4ever. Удачи!

UPD6: Онлайн-трансляция завершена! Поздравляем победителей:

1. rng_58
2. Zenith: I_love_Hoang_Yen, ngfam_kongu
3. OrOrZZZ!: zld3794955, KFDong
4. Petr team: Petr, ilyakor
5. jcvb_matthew99: matthew99, jcvb

Мой персональный респектам команде Petr team: Petr, ilyakor за единственное решение по задаче Е в трансляции, пользователю rng_58 и команде Excited: YuukaKazami, jqdai0815 за два правильных решения по задаче С.

Также, поздравляем пользователя rng_58, который продемонстрировал, что одиночному пользователю есть что противопоставить командам, состоящим из двух людей!

Рейтинг будет пересчитан в ближайшее время.

UPD7: Разбор!

VK Cup 2015 завершен! Это было что-то невероятное — частая смена лидеров, тяжелый ход контеста фаворита, посылки топовых команд на последних секундах!

Сегодня же вечером в торжественной обстановке в зале "Толстой" отеля Кортъярд Марриотт были подведены результаты.

• 1 место: команда из ИТМО в составе Геннадия «tourist» Короткевича и Нияза «niyaznigmatul» Нигматуллина — Чемпионы VK Cup 2015 и приз в 1048576 рублей,
• 2 место: команда из ИТМО в составе Адама «subscriber» Бардашевича и Бориса «qwerty787788» Минаева — приз в 524288 рублей,
• 3 место: команда из ИТМО в составе Ивана «Belonogov» Белоногова и Ильи «izban» Збаня — приз в 262144 рублей,
• 4 место: команда из Нижегородского ГУ в составе: Владислав «vepifanov» Епифанов (ННГУ) и Николай «KAN» Калинин
• 5 место: команда из Уральского ФУ в составе Ильи «KuchumovIlya» Кучумова и Олега «Merkurev» Меркурьева
• 6 место: команда из Московского ГУ в составе: Василия «SirShokoladina» Мокина и Глеба «GlebsHP» Евстропова
• 7 место: команда из Уральского ФУ в составе Алексея «Um_nik» Данилюка и Никиты «sivukhin» Сивухина
• 8 место: команда из МФТИ в составе Михаила «Endagorion» Тихомирова и Александра «map» Машрабова

Команды с 4-го по 8-е места завоевали призы в размере 131072 рублей! Все участники финала получили ценный подарок и сертификат финалиста.

Вот несколько фотографий с закрытия соревнования.

VK Cup 2015 - Finals состоится уже сегодня! Мы желаем удачи всем участникам, а болельщикам — насладится интересным соревнованием.

Лучшие 20 команд по результатам серии отборов собрались в Санкт-Петербурге, чтобы встретиться в финале и побороться за титул Чемпиона и солидный призовой фонд:

• 1 место — 1048576 рублей,
• 2 местo — 524288 рублей,
• 3 местo — 262144 рубля,
• 4-8 места — 131072 рубля.

Болеть за команды можно будет по ссылке http://mirror.codeforces.com/spectator/contest/562/standings, которая будет доступна после старта соревнования.

Удачи! Желаем только положительных эмоций. На старт! Внимание! ...

Всем привет!

Вчера, 24 июля, мы открыли финал VK Cup 2015! В течение дня к нам съехались все участники финала соревнования, а те из них, кто прибыл пораньше, успели насладиться прогулкой по крышам Санкт-Петербурга. А сегодня через пару часов состоится пробный тур, во время которого участники смогут познакомиться с условиями проведения финала и попробовать свои силы в решении пары обычных (и не совсем) задач. После обеда участников ждёт первый тур нашего соревнования, CodeGame Coding, в рамках которого им предстоит написать стратегию для управления боевым магом.

На время сегодняшнего и завтрашнего дня функциональность Codeforces будет по большей части урезана. В эти выходные вы можете отдохнуть от написания тренировок и насладиться результатами одного из крупнейших соревнований 2015 года по программированию.

Результаты пробного тура будут доступны для болельщиков по данному адресу. Ждите новостей от нас!

В воскресенье, 3-го мая, в 19:00 начнётся Раунд 3 чемпионата по программированию VK Cup 2015! Не забудьте зарегистрировать вашу команду на раунд, регистрация закроется за пять минут до его старта.

В этом раунде могут принять участие все те команды, которые отобрались в Раунде 2 или в Уайлд-кард раунде 2. Напомним, что из второго раунда допущены все те команды, что набрали не менее 928 баллов. В уайлд-кард раунде 2 было достаточно набрать 1827 баллов. Таким образом, принять участие в Раунде 2 могут 100 + 20 = 120 команд!

Участников ждет соревнование по правилам классических раундов Codeforces. Раунд 3 пройдёт в таком же формате, как и Раунд 2 — с онлайн-трансляцией, рейтинговой и доступной только для див-1 участников. Будет использована плавная динамическая система оценки задач, но сами задачи будут расположены в случайном порядке. Участникам будет предложено 6 задач.

Раунд подготовлен силами команды Codeforces, команды VK и пользователя yeputons. Как всегда, неоценимую помощь в тестировании задач оказали winger и AlexFetisov.

Напомним, что в Финал VK Cup пройдут все те команды, которые наберут положительный балл, не меньший, чем у команды на 20-м месте. Также обращаем ваше внимание, что участники всех команд, прошедших в Раунд 3 (независимо от их участия или неучастия в Раунде 3 или в его трансляции), получат фирменную футболку Чемпионата. Помимо этого, фирменной футболкой будут награждены топ-50 участников интернет-трансляции Раунда 3.

Желаем удачи и интересной борьбы!

UPD1 Раунд 3 завершён! Поздравляем топ-20 команд, которые отправятся в июле на Финал VK Cup 2015! Следите за объявлениями на сайте, точная информация о финальном раунде появится позднее.

UPD2 Тем временем появился разбор.

Сегодня, 18-го апреля в 21:00, начнется VK Cup 2015 - Уайлд-кард раунд 2.

Участникам раунда будет предложено максимально продвинуться в решении одной сложной и необычной задачи. Официально в этом раунде смогут принять участие команды чемпионата VK Cup 2015, которые прошли в Раунд 2, но не оказались среди тех топ-100 лучших по его результатам, кто проходит в Раунд 3. Кроме того, этот раунд будет открыт для всех желающих для неофициального участия вне чемпионата. Зарегистрироваться на раунд можно будет в любое время пока он идет.

Продолжительность раунда — одна неделя. После ее окончания мы выберем последнюю попытку, набравшую положительный балл, каждого из участников и проведем финальное тестирование.

Удачи!

UPD: Закончено системное тестирование. Тесты системного тестирования доступны по ссылке: http://assets.codeforces.com/files/vkcup-2015-wildcard-2-tests.2.zip

Вы можете присылать апелляции по содержанию тестов и ответов на них до 23:59:59 28-го апреля. После этого будут подведены официальные результаты и даже найденные потом проблемы в тестах не будут влиять на финальное положение участников

В пятницу, 17-го апреля, в 19:00 начнётся Раунд 2 чемпионата по программированию VK Cup 2015! Не забудьте зарегистрировать вашу команду на раунд, регистрация закроется за пять минут до его старта.

В этом раунде могут принять участие все те команды, которые отобрались в Раунде 1 или в Уайлд-кард раунде 1. Напомним, что из первого раунда допущены все те команды, что набрали не менее 796 баллов. В уайлд-кард раунде было достаточно решить не менее шести задач, либо решить пять задач со штрафным временем не более 415 минут. Таким образом, принять участие в Раунде 2 могут 400 + 50 = 450 команд!

Участников ждет соревнование по правилам классических раундов Codeforces. По сравнению с Раундом 1 вас ждут некоторые изменения. Во-первых, одновременно с основным раундом будет проведена интернет-трансляция, которая представляет из себя обычный рейтинговый div1-раунд по правилам Codeforces. В трансляции может участвовать любой div1-участник, не зарегистрированный на основной раунд в составе отобравшейся команды.

Во-вторых, вас, как и ранее, ждёт плавная динамическая система оценки задач, но сами задачи будут расположены в случайном порядке. Участникам будет предложено 6 задач.

Раунд подготовлен силами команды Codeforces, команды VK и пользователя Errichto, который предложил свою неоценимую помощь в рамках кампании "5 лет Codeforces". Большую помощь в тестировании задач оказал winger.

Напомним, что в Раунд 3 пройдут все те команды, которые наберут положительный балл, не меньший, чем у команды на 100-м месте. Также обращаем ваше внимание, что все команды, проходящие в Раунд 3, получат фирменную футболку Чемпионата. Помимо этого, фирменной футболкой будут награждены топ-50 участников интернет-трансляции Раунда 3.

Желаем удачи и интересной борьбы!

UPD: Благодарим всех за участие! Появился разбор задач. Ждём вас на Уайлд-кард раунде 2 и Раунде 3!

Язык этого раунда — Picat, во многом похожий на Prolog. Мы постарались подобрать задачи так, чтобы большинство из них было удобно решать с использованием декларативного подхода.

Традиционная программа A+B (числа A и B разделены пробелом) выглядит следущим образом:

main =>
  A = read_int(),
  B = read_int(),
  C = A + B,
  println(C).

Основной источник информации о языке — сайт http://picat-lang.org/. Используется версия 0.9.

В субботу, 21-го марта, в 17:00 будет дан старт Раунду 1 чемпионата по программированию VK Cup 2015! Не забудьте зарегистрировать вашу команду на раунд, регистрация закроется за пять минут до его старта.

В этом раунде могут принять все те команды, которые прошли квалификацию. Напомним, что из первой квалификации допущены все те команды, что набрали не менее 1500 баллов. Таких оказалось 789. Вторую квалификацию прошли 504 команды, все те, что набрали не менее 1850 баллов. Таким образом, принять участие в Раунде 1 могут 1293 команды!

Участников ждет соренование по правилам классических раундов Codeforces с некоторыми адаптациями:

• задачи будут исключительно на русском языке (в отличие от интернет-трансляции, где будут и на английском);
• в Раунде 1 будут участвовать команды по 1 или 2 человека, разрешается любая коммуникация внутри команды, но какое-либо общение с другими лицами по прежнему, конечно, запрещено;
• каждая команда может использовать один или более компьютеров по своему усмотрению (напомним, что в Финале команде будет дана возможность использовать только один компьютер);
• для членов команды рейтинг будет пересчитан одинаково, исходя из рейтинга команды (учитываются зарегистрированные на раунд члены команды), о подсчете рейтинга команды можно почитать здесь.

Участников ждет обновленная динамическая стоимость задач (смотрите пост), теперь более плавная, с шагом в 250 баллов.

Отметим, что сразу после окончания Раунда 1 будет проведена интернет-трансляция, поэтому просим участников воздержаться до ее окончания от публичных обсуждений, распространения информации о задачах, идеях и даже ходе соренования.

Напомним, что в Раунд 2 пройдут все те команды, которые наберут положительный балл не меньший, чем у команды на 400-м месте.

Желаем удачи и интересной борьбы!

UPD.: Раунд закончен, спасибо за проявленный интерес. Раунд получился динамичным, жюри с интересом следили за ходом соревнования. Поздравляем победителей и напоминаем, что лучшие 400 команд (т.е. те, кто набрал не менее 796 баллов) получают приглашение в Раунд 2. Остальным еще рано расстраиваться, ведь через неделю вас ждет Вайлд-кард 1, по результатам которого будут разыграны еще 50 приглашений в Раунд 2.

523A - Rotate, Flip and Zoom

Это была несложная задача на технику работы с двумерными массивами. Для решения задачи можно было честно последовательно проделать все три операции или заметить, что первые две (поворот + отражение) совместно дают простую транспозицию (отражение относительно главной диагонали, когда клетка с координатами (i, j) отображается на клетку с координатами (j, i)). Поэтому для вывода ответа было достаточно сделать два цикла (используется 0-индексация и псевдоязык):

for i = [0...2*a-1] begin
  for j = [0...2*b-1] begin
    print(a[i / 2][j / 2])
  end
  вывести перевод строки
end

Пример решения: 10286345.

523B - Mean Requests

Подсчет приближенного среднего подробно описан в условии задачи (даже приведен псевдокод). В самом деле при его подсчете надо было просто следовать описанным правилам подсчета.

Для подсчета среднего на отрезках длины T достаточно знать значение суммы элементов на отрезках длины T (для получения среднего надо просто значение суммы делить на T). Если это делать наивным способом, подсчитывая сумму каждый раз в цикле заново, то получается неэффективный медленный алгоритм. В самом деле, при T = n / 2 и наборе из m = n запросов n / 2 + 1, n / 2 + 2, ..., n такой алгоритм суммарно выполнит около n² / 4 действий. Для заданного максимального значения n эта величина будет слишком большой для вычисления в 4 секунды.

Для ускорения подсчета суммы на отрезках длины T можно либо поддерживать эту сумму, тогда при перемещении старта такого отрезка с индекса i на индекс i + 1 сумма изменяется следующим образом: sum:  = sum - a[i] + a[i + T]. Таким образом, пересчет суммы от предыдущего положения старта отрезка до нового будет работать за одну формулу (ограниченное сверху некоторой константой количество действий).

Второй вариант как быстро находить суммы на отрезках состоит в подсчете вспомогательного массива частичных сумм. Пусть b[i] — сумма первых i элементов массива a. Тогда сумма элементов массива a на отрезке от l до r равна b[r + 1] - b[l] (если массив a 0-индексирован). Подсчет массива b можно осуществить за один проход слева направо по формуле b[i] = b[i - 1] + a[i - 1].

Пример решения: 10291184.

523C - Name Quest

Наивный способ решения задачи (перебрать разрез и проверить "хорошесть" каждого из них) работает за квадратичное время и недостаточно эффективен, чтобы решение прошло.

Посчитаем две позиции:

• такую минимальную позицию l, что подстрока t[1..l] хорошая, тогда очевидно, что любой разрез за позицией l будет таким, что левая часть "хорошая",
• такую максимальную позицию r, что подстрока t[r..|t|] хорошая, тогда очевидно, что любой разрез перед позицией r будет таким, что правая часть "хорошая".

Каждую из величин l и r можно найти жадным образом просто итерируясь до вхождения очередной буквы и продолжая поиск следующей. Вот пример возможного кода для поиска l:

j := 1
for i := 1 to |t|
    if j <= |s| && s[j] == t[i]
        j = j + 1
        if j = |s| + 1
            l := i

Для того, чтобы после разреза обе части содержали s необходимо и достаточно, чтобы разрез проходил между l и r. Таким образом, ответ равен r - l или 0, если l или r не нашлось или r < l.

523D - Statistics of Recompressing Videos

Для эффективной реализации алгоритма моделирования процесса необходимо хранить в какой-то структуре h отсортированные моменты освобождения каждого из серверов. Сначала h состоит k единиц.

Будем обрабатывать ролики последовательно в хронологическом порядке. Для того, чтобы начать обрабатывать очередной i-й надо дождаться освобождения какого-либо сервера. Пусть ролик приходит в момент s_i и имеет длительность t_i.

Очевидно, что можно ждать освобождения до первого из моментов из h (так как первый — минимальный). Возможно, что дожидаться в явном виде и не надо, так как сервер уже освобождается к моменту s_i, в любом случае можно считать, что ролик надо отправить на первый из серверов, который освободиться. Пусть минимальный элемент из h равен h₀, тогда ролик начнется обрабатываться в момент max(h₀, s_i), а закончит к моменту max(h₀, s_i) + t_i. Для поддержания структуры h надо исключить из нее h₀ и добавить max(h₀, s_i) + t_i. Таким образом, в h по прежнему будут все моменты освобождения серверов.

Для того, чтобы решения быстро работали, h надо хранить в подходящей структуре данных. Это может быть очередь с приоритетами (тогда минимум будет в голове), либо в упорядоченном множестве. Так как в h могут быть равные элементы, то эта структура либо должна работать с одинаковыми элементами (как очередь с приоритетами или мультимножество по типу std::multiset в C++) или надо в структуре хранить пары (момент освобождения, номер сервера).

Кроме того в качестве h можно использовать классическую бинарную кучу или упорядоченный ассоциативный массив (TreeMap в Java).

Такое решение будет работать за .

Пример решения: 10290987. В этом решении в очереди с приоритетами q моменты хранятся со знаком минус, чтобы сортировка по-умолчанию ставящая максимум вперед, ставила вперед минимум.

14 марта в 18:00 начнется второй квалификационный раунд чемпионата VK Cup 2015!

Правила этого раунда будут совпадать с Квалификацией 1. К участию приглашаются те команды, кто не участвовал в Квалификации 1 или набрал менее 1500 баллов в ней.

Раунд продлится 24 часа, такая продолжительность выбрана для того, чтобы все нашли себе удобное время для участия. Квалификационный раунд, как и все предстоящие раунды, требует отдельной регистрации, она будет открыта на протяжении всего раунда.

При регистрации на раунд состав вашей команды фиксируется и не подлежит дальнейшей модификации. Вы не сможете в будущем добавить или удалить члена команды. Пожалуйста, перед регистрацией убедитесь, что у вас нет желания изменить состав. Состав команды не сможет быть изменен, даже если вы отмените регистрацию на квалификационный раунд.

В Раунд 1 пройдут все те команды, которые набрали положительный балл и одновременно не меньший, чем у 500-го места.

Во время квалификации задачи тестируются системой только на претестах, а системное тестирование состоится после окончания раунда. Обратите внимание, что претесты не покрывают все возможные случаи входных данных, поэтому тщательно тестируйте свои программы! Взломов, падения стоимости задач во время квалификации не будет. Время сдачи задач не будет учитываться, однако будут учитываться штрафные попытки.

Категорически запрещается публиковать где-либо условия задач/решения/какие-либо мысли и соображения о них до окончания раунда. Запрещено обсуждать задачи с кем-либо кроме вашего сокомандника. Будьте честны, пусть в Раунд 1 пройдут сильнейшие!

Результаты раунда не будут влиять на рейтинг. Уже прошедшие в Раунд 1 команды, могут участвовать в Квалификации 2 вне конкурса. Они никак не влияют на отбор участников в Раунд 1, они могут участвовать только just for fun. Внеконкурсное участие тоже требует соблюдение всех правил, в случае нарушения команда может быть дисквалифицирована с Чемпионата.

После окончания раунд станет доступен всем для дорешивания, а его задачи попадут в архив в том числе и на английском языке.

522A - Reposts

Для решения этой задачи надо было проитерироваться по записям о репостах и поддерживать для каждого пользователя длину цепочки, которая заканчивается в нем. Здесь удобно воспользоваться ассоциативным массивом из строки (имени пользователя) в целое число (длину цепочки). Например, для С++ такой структурой данных будет просто map<string,int>. Назовем такую структуру chainLengths, тогда при обработки строки вида <<a reposted b>> надо просто выполнить присвоение chainLengths[a] = chainLengths[b] + 1. В качестве ответа надо вывести максимальное из значений chainLengths, что можно подсчитывать на лету.

Пара тонкостей: в начале надо занести chainLengths["polycarp"] = 1;, а всюду при работе со строками приводить их к нижнему регистру (или верхнему), чтобы сделать сравнение строк нечувствительным к регистру букв.

Пример такого решения: 10209456.

522B - Photo to Remember

В этой задаче для каждого i фактически надо было найти:

• W_i, равное сумме всех заданных w_j без w_i,
• и H_i, равное максимуму всех h_j без h_i.

Для подсчета первой величины достаточно найти сумму s всех значений w_j, тогда W_i = s - w_i.

Для подсчета второй величины достаточно заметить, что либо искомое значение есть просто максимум по h, либо (если h_i совпало с максимумом) это второй максимум (т.е. предпоследний элемент при сортировке по неубыванию). Второй максимум, как и максимум ищется за один проход по массиву.

В таком случае, для нахождения как W_i, так и H_i требуется O(1) действий, то есть O(n) суммарно на всё решение.

Пример решения: 10193758.

522C - Chicken or Fish?

Для решения задачи необходимо заметить, что при наличии недовольных пассажиров (т.е. тех, для кого r_i = 1), существенную роль играет только первый из них, так как остальные вполне могут быть недовольными именно тем блюдом, которое не хватило первому из таковых.

Пусть массив b — это массив максимальных возможных количеств порций каждого из блюда на момент старта обслуживания Поликарпа. То есть просто массив b надо заинициализировать массивом a, а каждый раз, когда t_i отлично от 0, то делать b[t_i] = b[t_i] - 1 (уменьшать количество порций блюда). Кроме того, пусть unknown — это количество пассажиров, про которых неизвестно какие точно блюда им достались (то есть для них t_i = 0). Пусть величина unknownBeforeUpset — это такое же количество, но до первого недовольного.

Таким образом, есть два основных случая:

• недовольных пассажиров нет вообще, тогда блюдо i могло закончится тогда и только тогда, когда b[i] ≤ unknown (жадно отдаем это блюдо всем пассажирам, для кого их точное блюдо неизвестно),
• недовольный пассажир есть, этот случай разберем подробнее.

Каким блюдом мог быть недоволен первый из таких пассажиров? Очевидно из списка кандидатов надо выкинуть все такие блюда, которые упоминаются не раньше него (значит, что они закончится до него не могли). Из оставшегося набора блюд достаточно перебрать все блюда и проверить могли ли они закончиться до этого пассажира. То есть блюдо i могло быть тем блюдом, что привело в недовольство первого недовольного, если одновременно верно:

• это блюдо i не упоминается на этом пассажире или позже,
• это блюдо i такое, что b[i] ≤ unknownBeforeUpset.

Для всех таких блюд, очевидно, в ответе должно стоять Y (они могли закончится к Поликарпу). Кроме того, из всех таких блюд наибольшую степень свободы дает блюдо с наименьшим расходом (количеством порций b[i]). Выберем именно такое блюдо и в остаток пассажиров с неизвестным блюдом restUnknown = unknown - b[minFirstFinished] попробуем поместить все вхождения каждого из других блюд. То есть блюдо j могло закончится до Поликарпа тогда и только тогда, если для него b[j] ≤ restUnknown (то есть закончилось то блюдо, что расстроило первого из недовольных, а следом — j-е).

Такое решение работает за O(m + k).

Пример решения: 10212686.

522D - Closest Equals

Воспользуемся тем, что задача задана в офлайн-формулировке, то есть все запросы можно считать до нахождения ответов на них.

Пройдем слева направо по массиву и составим новый массив b, записав в b[j] расстояние до ближайшего слева парного j-му элементу значения, то есть a[j - b[j]] = a[j]. Если такового нет, то запишем в ячейку бесконечность.

Эти значения соответствуют расстояниям между парными элементами и записаны они в позициях правых элементов в этих парах.

При рассмотрении запроса на отрезке [l, r] нам не нужны вообще такие пары, что начинаются левее l, а минимум надо искать среди пар, что заканчиваются не правее r.

Отсортируем все запросы по l слева направо. Тогда при прохождении по запросам можно поддерживать, что для запроса [l, r] в массиве b установлены бесконечности для всех пар, в которых левый элемент левее l. Для этого просто предподсчитаем для каждого элемента ближайший справа парный next[i] (то есть верно, что b[next[i]] = next[i] - i), и при покидании ячейки i будем записывать в b[next[i]] значение бесконечность.

В таком случае, для ответа на запрос [l, r] надо просто найти минимум на префиксе до индекса r включительно по массиву b. Это можно делать быстро разными способами (дерево отрезков, дерево Фенвика).

Асимптотическая временная сложность такого решения составляет .

Пример решения: 10192075.

Всем привет!

7 марта в 18:00 начнется первый квалификационный раунд чемпионата VK Cup 2015!

Раунд продлится 24 часа, такая продолжительность выбрана для того, чтобы все нашли себе удобное время для участия. Квалификационный раунд, как и все предстоящие раунды, требует отдельной регистрации. Регистрация станет доступна 7 марта в 00:00, она будет открыта на протяжении всего раунда.

При регистрации на любой из квалификационных раундов состав вашей команды фиксируется и не подлежит дальнейшей модификации. Вы не сможете в будущем добавить или удалить члена команды. Пожалуйста, перед регистрацией убедитесь, что у вас нет желания изменить состав. Состав команды не сможет быть изменен, даже если вы отмените регистрацию на квалификационный раунд.

Если вы пока не уверены в текущем составе команды, то не регистрируйтесь на предстоящий раунд. Если вы не будете участвовать в первой квалификации или не пройдете по ее результатам в Раунд 1, то вы сможете попробовать свои силы во второй квалификации.

Чтобы пройти в Раунд 1, вам надо принять участие хотя бы в одной из квалификаций. Из каждой квалификации в Раунд 1 проходят все команды с положительным числом баллов, которые набрали не меньше баллов, чем команда на 500-ом месте.

Пользуясь случаем поздравляем всех девушек-участниц с праздником. Спасибо вам за весну!

Во время квалификации задачи тестируются системой только на претестах, а системное тестирование состоится после окончания раунда. Обратите внимание, что претесты не покрывают все возможные случаи входных данных, поэтому тщательно тестируйте свои программы! Взломов, падения стоимости задач во время квалификации не будет. Время сдачи задач не будет учитываться, однако будут учитываться штрафные попытки.

Категорически запрещается публиковать где-либо условия задач/решения/какие-либо мысли и соображения о них до окончания раунда. Запрещено обсуждать задачи с кем-либо кроме вашего сокомандника. Будьте честны, пусть в Раунд 1 пройдут сильнейшие!

Результаты раунда не будут влиять на рейтинг, внеконкурсное участие в раунде не разрешается. Однако, после окончания раунд станет доступен всем для дорешивания, а его задачи попадут в архив в том числе и на английском языке.

Добрый день, Codeforces!

Мы рады сообщить вам, что в этом году компания ВКонтакте совместно с площадкой Codeforces проведет обновленный VK Cup. Во многих IT-компаниях, в том числе и ВКонтакте, широко применяется практика парного программирования. VK Cup 2015 предлагает участникам попробовать именно такой формат, допуская к участию команды до двух человек. За призы и звание победителя приглашается побороться русскоязычным молодым специалистам, студентам, школьникам и просто любителям алгоритмов и программирования.

Лучшие 20 команд по результатам отборочных интернет-этапов будут приглашены в финал соревнования, который состоится в июле 2015-го года в Санкт-Петербурге. Компания ВКонтакте покроет расходы на проезд и проживание финалистов, которые будут бороться не только за звание лучших из лучших, но и призовой фонд чемпионата. В этом году мы сделали призы соревнования круглыми числами в двоичной системе счисления:

• 1 место — 1048576 рублей
• 2 местo — 524288 рублей
• 3 местo — 262144 рубля
• 4-8 места — 131072 рубля

Hi Codeforces!

The VK company (vk.com), the largest social network in Europe and the most popular site in Russia and Ukraine, announces the competition for russian-speaking programmers VK Cup 2015.

As you can see, the reborn VK Cup is focused on Russian-speaking programming lovers. Indeed, the whole VK developer team speaks Russian, most social network users communicate in Russian and the head office of the company is located in St. Petersburg. Those are the reasons we decided to concentrate on the competition for russian-speaking participants — most of the social network code is written by medal winners and ACM-ICPC finals champions. We believe that when we support the enthusiasm of young people towards solving problems and studying algorithms, that we make the world better and invest for the future of our company.

That is not the only innovation of the championship: unlike many other championships conducted by companies, VK Cup 2015 will have two-man teams competing with each other, the participants’ age ranges from 14 to 23 years.

Though we focus on the Russian-speaking participants, we are happy to share our problems and rounds with the participants from the whole world. For that reason, all problems of the championship will be translated into English and will be available to solve after the official championship rounds are over. Besides, in some rounds the participants from around the world can take part unofficially, side by side with the official championship contestants. We will be happy to give out 50 brand T-shirts of the Championship to the best out of competition unofficial participants of Round 3. We will be happy to see interest towards the problems of our championship!

VK Team