Hey guys,
Recently I faced an interesting problem which took me about couple of days of thinking but I couldn't find out the polynomial time solution. So I decided to share it with you:
Let
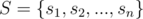 0 ≤ si ≤ 3
0 ≤ si ≤ 3
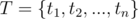 0 ≤ ti ≤ 1
0 ≤ ti ≤ 1
Now we want to Change the elements of S in a way that the following conditions are fulfilled:
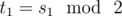
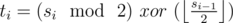 2 ≤ i ≤ n
2 ≤ i ≤ n
The only operations allowed are to increase or decrease si by 1 or let it to be unchanged. The goal is to find the minimum number of increasing or decreasing operations which satisfy the above equations for S and T. This task can be simply done using the Dynamic Programming in O(n) for any given S and T.
The main Problem is "what is the expected value of minimum operations for every given n?". The first Idea is to generate every Sequence of S and T for a given n, after computing the minimum operations for each pair, calculate the expected or average value. but this runs in O(n8n). Is there a polynomial time algorithm like DP for solving this task?










