I recently know about Strassen's aproach in multiplying matrices, which i find very clever and interesting. So i decided to share it. Hope this help :))).

People usually use the naive n^3 method to multiply a n*x and y*n matrix. Which mean the maximum size of n is about 500. But Strassen find a way to do so in n^log2(7) which is about n^2.8, which mean it will bring the maximum size of n to about 750. First, we divide the matrix in to smaller matrix.

Let consider a 2*2 matrix.

The result of this matrix will be:

And if A,B,C,D,E,F,G,H are all matrices of size n*n, it is still remain correct.

So we will multiply these matrices by using divide and conquer, divide them into smaller pieces and conquer them. Each time we multiply two matrices, we divide them into 2*2 matrices and calculate them.

Let consider a 2*2 matrix, regularly we need 8 multiplications to multiply 2 2*2 matrix.

But Strassen find a way to do so in just 7 multiplications so it will reduce the complexity from n^log2(8))(which is n^3) to n^log2(7).

So now i will describe the way he multiply 2*2 matrices with 7 multiplications.

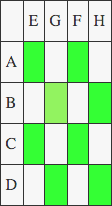
The figure above is a representation of the matrices multiplication i have show you earlier. Normally, we multiply each of the 8 green square to calculate the four sum of the matrix. To do so in 7 multiplication and then calculate the sum of each quarter separately we must think outside of the box and divide them differently (i honestly don't know how the heck Strassen came up with this). Strassen way of divide it look like this:

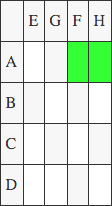
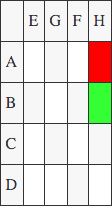
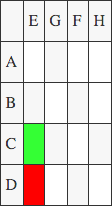
(In the following figure, green indicate a positive product and red is negative)

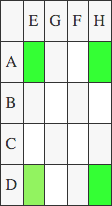
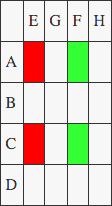
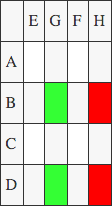
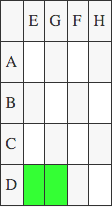
M1: (A+D)*(E+H)

M2: (F-E)*(A+C)

M3: (G-H)*(B+D)

M4: D*(E+G)

M5: A*(F+H)

M6: H*(B-A)

M7: E*(C-D)

The final result will be:

Although Strassen algorithm use less multiplication, it use many more addition and subtraction compare to the naive approach, so it is better with n>100.

UPD:Also, this only work with (2^x)*(2^x) matrix so you need to fill the space with 0 until it become a (2^x)*(2^x) matrix before doing the multiplication.

Hope this blog help, if i make any mistake please tell me.