Background
I have recently stumbled across a paper which analyzed the correlation between the IMO medal and future success in the mathematical field. So, inspired by annual predictions of IOI rankings based on CF ratings, I don't know what to do with my time decided to take a more "serious" approach.
Method
I collected the data from the last $$$7$$$ editions of IOI in order to create the graph of $$$f(x)$$$ is the maximal rating of the participant with rank $$$x$$$. For the last $$$6$$$ editions, I relied almost solely on the IOI statistics website. The $$$2012$$$ edition, however, is missing a lot of information and I collected the CF handles either from snarknews or by finding the handle on search engines.
I put the participants in the same order they were arranged in the scoreboard, so if there are multiple people on the same position, they would be assigned consecutive ranks. In case there was an unofficial participant, I assigned the mean of the ranks between which this participant was situated.
If there were participants with no competitions, I assigned the rating $$$1500$$$. This should not have big influence on the graph because there were very few such participants.
Things to consider:
A lot of participants from past editions don't participate in CF round anymore
The rating system has undergone inflation.
The rating system fluctuates too much.
The style/difficulty/originality of CF problems highly depends on the round and unlike the AtCoder case this creates disproportionality of rating distribution. So do the div 2/div 3/educational rounds.
Not everybody is active in CF rounds.
IOI 2012
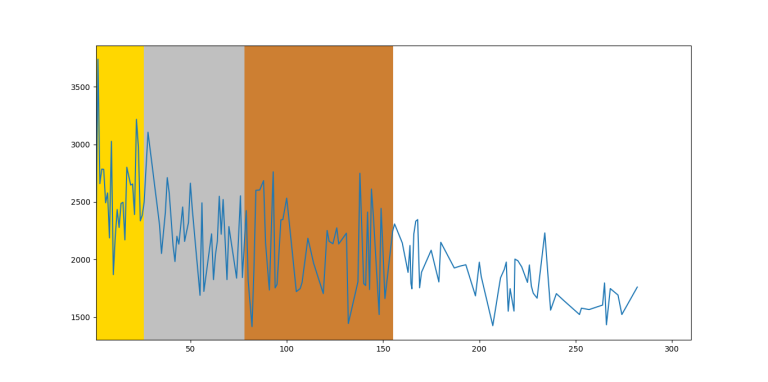
IOI 2013
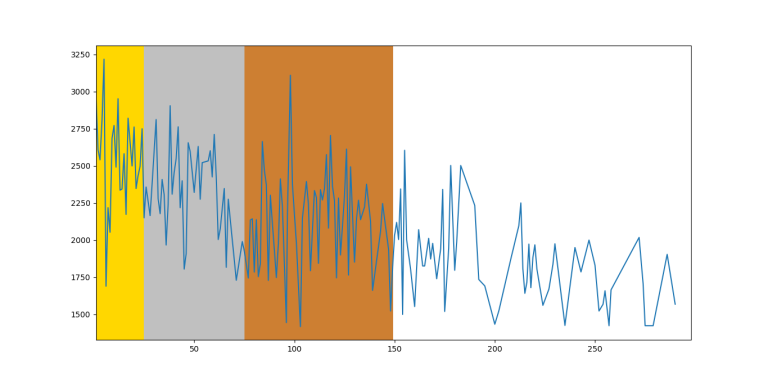
IOI 2014
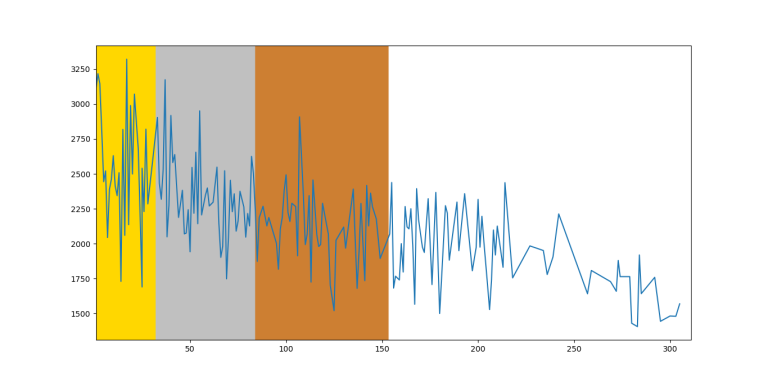
IOI 2015
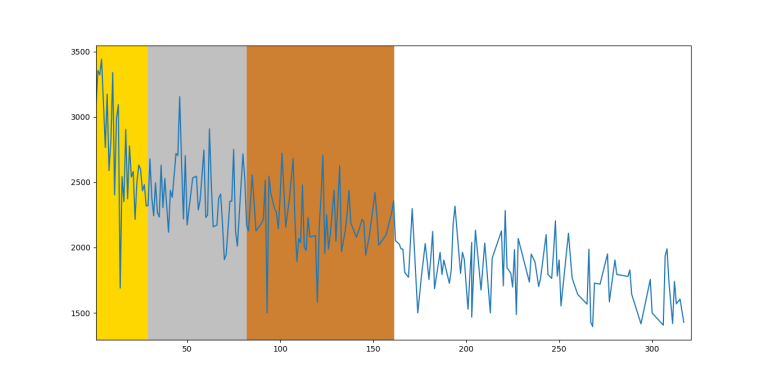
IOI 2016
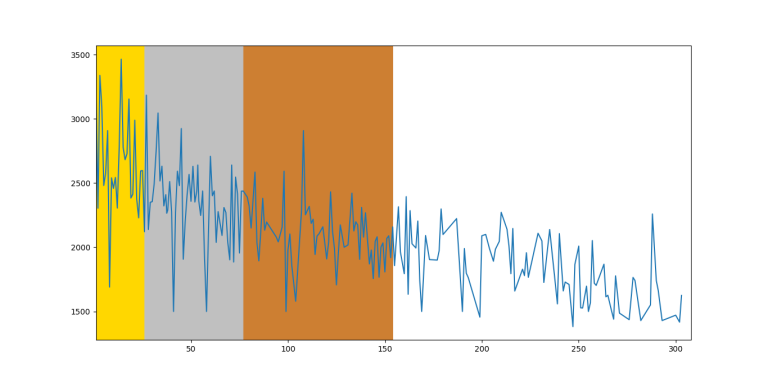
IOI 2017
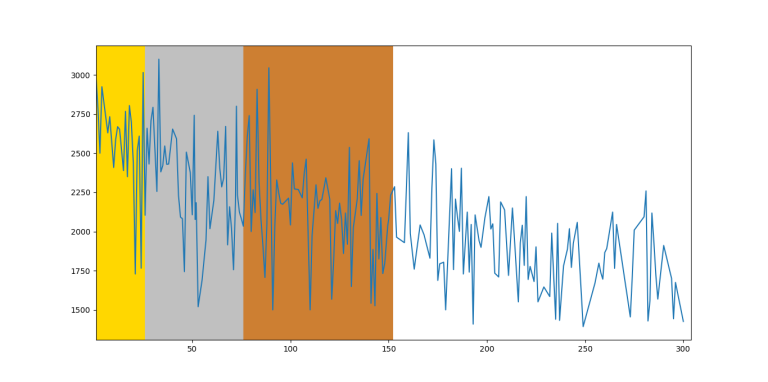
IOI 2018
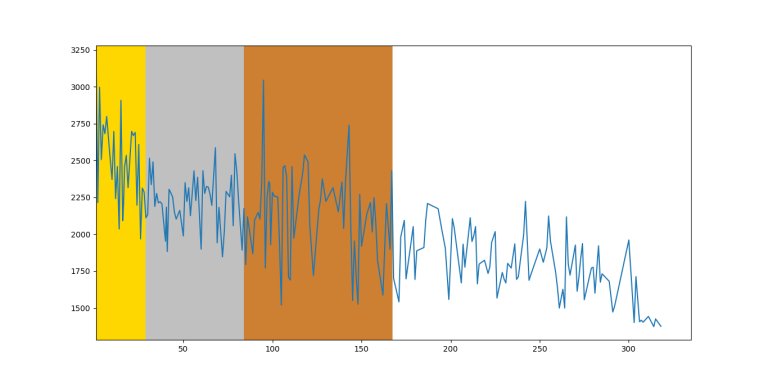
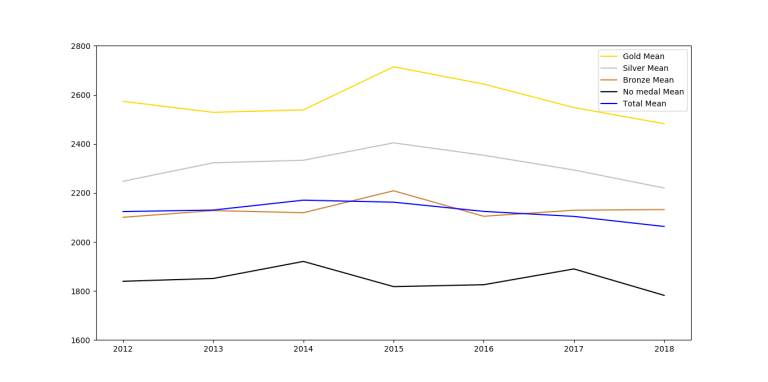
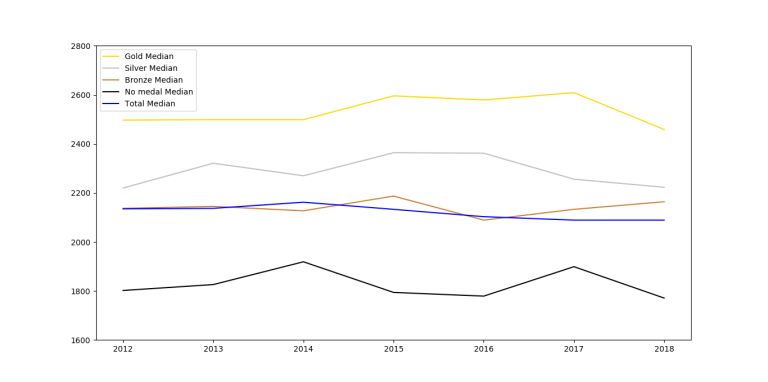
Conclusion
So, unsurprisingly, on average you can see that the function is decreasing by rank, however it fluctuates too much between close ranks. Therefore, on an individual level, you can't predict someone's future rating based on IOI ranking.
What do you think about this?








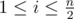 such that
such that 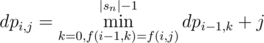 .
.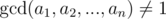 then the answer is
then the answer is 
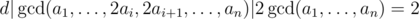 , so the gcd of the sequence can become at most
, so the gcd of the sequence can become at most 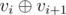 . Find the minimal number of moves to make the whole sequence equal to
. Find the minimal number of moves to make the whole sequence equal to 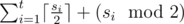 .
.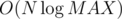 .
.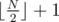 . First suppose that
. First suppose that  .
. What if you have
What if you have 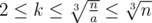 , so for each
, so for each 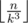 . Considering this, the final answer is
. Considering this, the final answer is 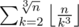 .
.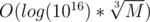 , Space:
, Space: 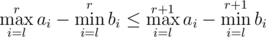 . So we can just use binary search to find the smallest index
. So we can just use binary search to find the smallest index  time and
time and 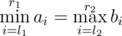 .
.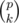 times,so our task reduce to calculate how many points is intersected by
times,so our task reduce to calculate how many points is intersected by 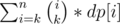 . We can easily calculate array
. We can easily calculate array 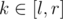 where
where 
