We realize that $$$n$$$ isn't too large in this version of the problem. First thing that comes to mind is using brute force. We'll simply check the sum of every single subarray and check if it's equal to $$$0$$$. An $$$O(n ^ 3)$$$ solution won't suffice so instead we'll have to write an $$$O(n ^ 2)$$$ one. We'll also have to make sure that the variable keeping track of our sum is of type long long since the values of $$$a_{i}$$$ reach up to $$$10^9$$$, meaning int would overflow.
#include <bits/stdc++.h>
using namespace std;
#define IAMSPEED ios_base::sync_with_stdio(0); cin.tie(0);
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
#define getrand(l, r) uniform_int_distribution<int>(l, r)(rng)
const int mod = 1000000007;
const int oo = 1000000010;
const int N = 1010;
int n, arr[N];
void solve(){
cin >> n;
for(int i = 0; i < n; ++i){
cin >> arr[i];
}
int ans = 0;
for(int i = 0; i < n; ++i){
long long sum = 0;
for(int j = i; j < n; ++j){
sum += arr[j];
if(sum == 0){
ans++;
}
}
}
cout << ans << '\n';
}
int main(){
IAMSPEED
int t = 1;
cin >> t;
while(t--){
solve();
}
return 0;
}
An $$$O(n ^ 2)$$$ solution is no longer sufficient here. Instead we'll have to find a more efficient method to solve the problem.
Given a precomputed cumulative sum array, we can calculate the sum of a subarray $$$[l, r]$$$ by $$$sum[r] - sum[l - 1]$$$. Now we want to count the subarrays such that $$$sum[r] - sum[l - 1] = 0$$$. Rearranging the terms leads us to $$$sum[r] = sum[l - 1]$$$. We can now rephrase the problem to the following: count the number of subarrays $$$[l, r]$$$ such that $$$sum[r] = sum[l - 1]$$$.
This makes the problem a lot simpler! We are now going to iterate over each $$$r$$$ and count the number of $$$(l - 1)$$$'s behind it such that $$$sum[r] = sum[l - 1]$$$. We can keep track of the frequency of each $$$sum[l - 1]$$$ using a frequency map.
#include <bits/stdc++.h>
using namespace std;
#define IAMSPEED ios_base::sync_with_stdio(0); cin.tie(0);
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
#define getrand(l, r) uniform_int_distribution<int>(l, r)(rng)
const int mod = 1000000007;
const int oo = 1000000010;
const int N = 100010;
int n, arr[N];
map<long long, int> cnt;
void solve(){
cin >> n;
for(int i = 0; i < n; ++i){
cin >> arr[i];
}
cnt.clear();
cnt[0]++;
long long ans = 0, pre = 0;
for(int i = 0; i < n; ++i){
pre += arr[i];
ans += cnt[pre];
cnt[pre]++;
}
cout << ans << '\n';
}
int main(){
IAMSPEED
int t = 1;
cin >> t;
while(t--){
solve();
}
return 0;
}
This was initially intended to be a very difficult problem to solve, but later realized that there's a much simpler solution to it (but still difficult enough).
The simpler solution can be implemented using a sliding window. We will iterate over every $$$r$$$ and find the minimum $$$l$$$ such that the range $$$[l, r]$$$ satisfies the condition. When the minimum $$$l$$$ has been found, we will then add every valid subarray ending with $$$r$$$ to our answer $$$([l, r], [l + 1, r], [l + 2, r], \dots, [r, r]) = r - l + 1$$$. We will keep track of the values in the current sliding window using a multiset in order to both check if the condition has been satisfied yet and for efficient retrieval, insertion and removal.
A sliding window works for this problem since if a range $$$[l_{1}, r_{1}]$$$ is valid and $$$l_{1} \le l_{2} \le r_{2} \le r_{1}$$$ then $$$[l_{2}, r_{2}]$$$ is definitely valid.
#include <bits/stdc++.h>
using namespace std;
#define IAMSPEED ios_base::sync_with_stdio(0); cin.tie(0);
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
#define getrand(l, r) uniform_int_distribution<int>(l, r)(rng)
const int mod = 1000000007;
const int oo = 1000000010;
const int N = 200010;
int n, k, arr[N];
void solve(){
cin >> n >> k;
for(int i = 0; i < n; ++i){
cin >> arr[i];
}
multiset<int> s;
int l = 0;
long long ans = 0;
for(int i = 0; i < n; ++i){
s.insert(arr[i]);
while(*s.rbegin() - *s.begin() > k){
s.erase(s.find(arr[l]));
l++;
}
ans += i - l + 1;
}
cout << ans << '\n';
}
int main(){
IAMSPEED
int t = 1;
cin >> t;
while(t--){
solve();
}
return 0;
}
#include <bits/stdc++.h>
using namespace std;
#define IAMSPEED ios_base::sync_with_stdio(0); cin.tie(0);
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
#define getrand(l, r) uniform_int_distribution<int>(l, r)(rng)
const int mod = 1000000007;
const int oo = 1000000010;
const int N = 100010;
int n, k, arr[N], mn[4 * N], mx[4 * N];
void build1(int c, int s, int e){
if(s == e){
mn[c] = arr[s];
return;
}
build1(2 * c, s, (s + e) / 2);
build1(2 * c + 1, (s + e) / 2 + 1, e);
mn[c] = min(mn[2 * c], mn[2 * c + 1]);
}
void build2(int c, int s, int e){
if(s == e){
mx[c] = arr[s];
return;
}
build2(2 * c, s, (s + e) / 2);
build2(2 * c + 1, (s + e) / 2 + 1, e);
mx[c] = max(mx[2 * c], mx[2 * c + 1]);
}
int get1(int c, int s, int e, int l, int r){
if(s > r || e < l) return oo;
if(s >= l && e <= r) return mn[c];
return min(get1(2 * c, s, (s + e) / 2, l, r), get1(2 * c + 1, (s + e) / 2 + 1, e, l, r));
}
int get2(int c, int s, int e, int l, int r){
if(s > r || e < l) return -oo;
if(s >= l && e <= r) return mx[c];
return max(get2(2 * c, s, (s + e) / 2, l, r), get2(2 * c + 1, (s + e) / 2 + 1, e, l, r));
}
void solve(){
cin >> n >> k;
for(int i = 1; i <= n; ++i){
cin >> arr[i];
}
build1(1, 1, n);
build2(1, 1, n);
long long ans = 0;
for(int i = 1; i <= n; ++i){
int idx = i;
for(int j = n; j > 0; j >>= 1){
while(idx + j <= n && get2(1, 1, n, i, idx + j) - get1(1, 1, n, i, idx + j) <= k){
idx += j;
}
}
ans += idx - i + 1;
}
cout << ans << '\n';
}
int main(){
IAMSPEED
int t = 1;
cin >> t;
while(t--){
solve();
}
return 0;
}
This was my favorite question out of the lot as I pinky promised El-Sisi that he'd love it and I never break my pinky promises.
Lets take an arbitrary cell in the grid with coordinates $$$(i, j)$$$ with value $$$x$$$:
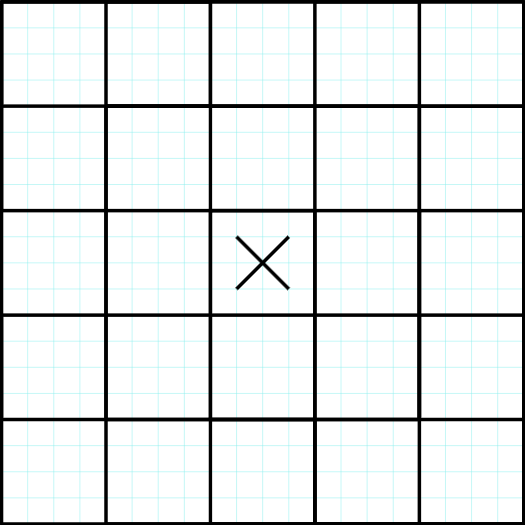
Now since every pair of adjacent cells has to give the same product then $$$(i + 1, j), (i - 1, j), (i, j + 1), (i, j - 1)$$$ must all have the same value, let's call it $$$O$$$:
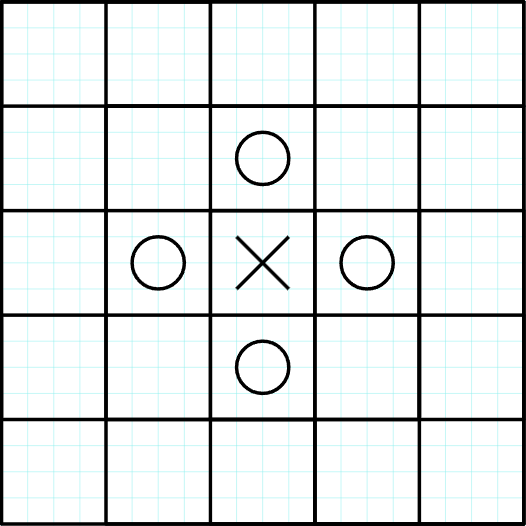
We have now decided that the product of any pair of adjacent cells must be $$$XO$$$. If we move on to the $$$O$$$ cells we will now have to assign $$$X$$$ to all adjacent cells in order for the product to be $$$XO$$$:
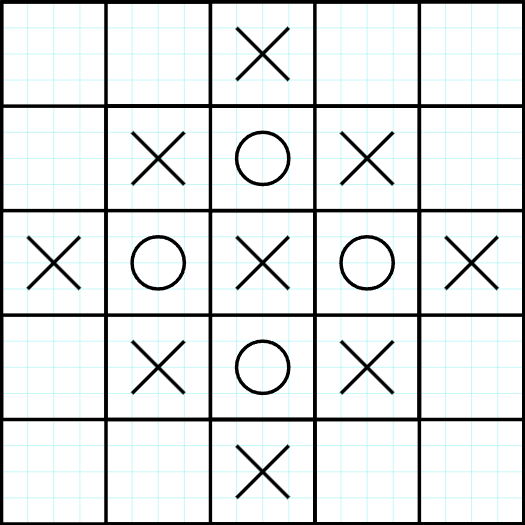
If we apply the same thing to all cells we will reach to the following:
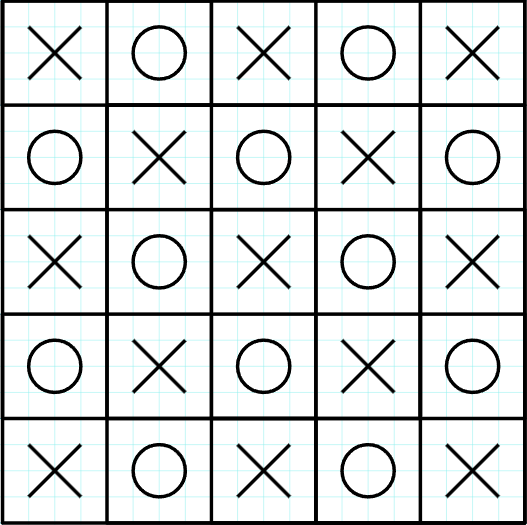
We reach to something that looks like a chess board. All black cells must have the same value $$$X$$$ and all white cells must have the same value $$$O$$$. There's a small edge case being when either $$$X$$$ or $$$O$$$ is equal to $$$0$$$. In this case it doesn't matter what the other value is because multiplying any value with $$$0$$$ will yield $$$0$$$.
As for the implementation, we need to keep track of the values in the black cells and the white cells. Determining what color $$$(i, j)$$$ is, can be done by checking whether $$$(i + j) \% 2$$$ is equal to $$$0$$$ or $$$1$$$. All that remains is using a suitable data structure to handle the queries in an efficient way. In this case a multiset is what we'll go with for quick retrieval, insertion and removal.
#include <bits/stdc++.h>
using namespace std;
#define IAMSPEED ios_base::sync_with_stdio(0); cin.tie(0);
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
#define getrand(l, r) uniform_int_distribution<int>(l, r)(rng)
const int mod = 1000000007;
const int oo = 1000000010;
const int N = 510;
int n, m, q, arr[N][N];
multiset<int> s[2];
void solve(){
cin >> n >> m >> q;
for(int i = 1; i <= n; ++i){
for(int j = 1; j <= m; ++j){
cin >> arr[i][j];
s[(i + j) % 2].insert(arr[i][j]);
}
}
while(q--){
int i, j, x;
cin >> i >> j >> x;
auto it = s[(i + j) % 2].find(arr[i][j]);
s[(i + j) % 2].erase(it);
arr[i][j] = x;
s[(i + j) % 2].insert(x);
bool ok = false;
ok |= (s[0].empty() || s[1].empty());
ok |= (!s[0].empty() && *s[0].rbegin() == 0);
ok |= (!s[1].empty() && *s[1].rbegin() == 0);
ok |= (!s[0].empty() && *s[0].begin() == *s[0].rbegin() && !s[1].empty() && *s[1].begin() == *s[1].rbegin());
cout << (ok ? "REEF" : "EL-SISI") << '\n';
}
}
int main(){
IAMSPEED
int t = 1;
// cin >> t;
while(t--){
solve();
}
return 0;
}









