Today we were solving probability problems in class when suddenly the schoolmaster came, opened the door and said the president was coming. A few moments later, the president entered the class and greeted us and visited school! Imagine that you are solving a problem in class on an ordinary day when suddenly the president of your country walks into the class.
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3977 |
| 2 | tourist | 3815 |
| 3 | jqdai0815 | 3682 |
| 4 | ksun48 | 3614 |
| 5 | orzdevinwang | 3526 |
| 6 | ecnerwala | 3514 |
| 7 | Benq | 3483 |
| 8 | hos.lyric | 3381 |
| 9 | gamegame | 3374 |
| 10 | heuristica | 3358 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 170 |
| 2 | -is-this-fft- | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 160 |
| 5 | djm03178 | 157 |
| 6 | Dominater069 | 156 |
| 7 | adamant | 154 |
| 8 | luogu_official | 152 |
| 8 | awoo | 152 |
| 10 | TheScrasse | 147 |
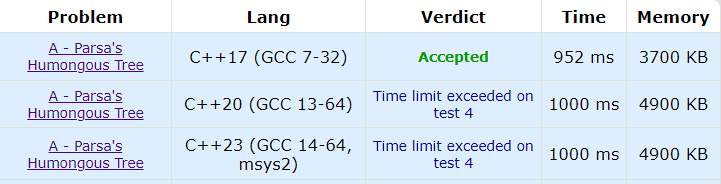
The same code on different versions of C++, but only C++17 gets AC. Old but Gold!
In the New Year, we can set our rank to Tourist by magic, if Mike add it to that list
Here is my view when coding :)

Hello there!
Today is Persian New Year's day, Nowruz!
I wish this year be an amazing year for you!
I hope to see all you in RED...
Happy Nowruz!

Binary Search
Hello everyone!
Today I'm going to talk you about a useful problem-solving method, binary search. If you have seen, in some problems we can't use an algorithm with $$$O(n^2)$$$ (because your program would be too slow to solve such problems). In those cases, you can use faster algorithms, but one of the popular algorithm is binary search. In binary search, you assume an integer as the answer, and you try that to see if it is the real answer or not. In this algorithm, you have an answer range, with usually starts with 0 and the end of the range will be maximum possible answer (i.g. 1e9). Let's play a game to understand better. One of your friends choose an integer from 1 to 100 and you need to ask some questions of your friend to find the number your friend had chosen. If you work smart (you will because you are smart) you start with this question: Is it less than 50? Do you agree if the friend's answer is yes, your range will be divided by 2 and also if your friend's answer is no. We assume he/she said NO, then you choose the number that is in the middle to work more efficiently, so you choose 25 and until you trap 1 exact integer, which is the answer!
Binary search is so similar to this game. You choose the middle integer in your current range, and check it. Let's calculate the order of algorithm. We assume you divide the range $$$x$$$ times, then $$$x$$$ would be $$$⌈log2(x)⌉$$$, because you it divides by 2 at most $$$⌈log2(x)⌉$$$ times! So the binary search is $$$O(⌈log(n)⌉)$$$.
Here's a simple code of binary search game:
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n; //assume we don't know the answer is n
int left = 1, middle, right = 101; //defining left and right of the range
while(left < right - 1) { //because our program does not check 101 and more!
middle = (left + right) / 2; //getting the middle of the current range
if (middle <= n) { //here is the question: is my guess less than the answer?
left = middle; //if yes, remove the left part of current range by moving the pointer
}
else {
right = middle; //and also similar thing for this
}
}
cout << "The answer is " << left; //finally we have found the exact answer
}
I explained the game in detail in the code comments ;)
Binary search is optimal algorithm to solve a lot of problems, so if you didn't know how to solve some problems without "Time limit exceeded", then try this!
Hope you enjoy my entry, please make me happy by clicking this little green button below :)
Thanks codeforces!
//This tutorial is just for begginers!
Happy New Year 2024 to all people around the world including Codeforces users! ;)
Please make me happy by giving me like on this entry <3 Thanks!
Hi everyone! I want to find the formula which changes the ratings. Does anyone know the formula for rates? (By contest Div, old rating and count of Accepted problems) Thanks!
| Name |
|---|










