895A - Pizza Separation
Заметим, что если один из секторов непрерывен, то все оставшиеся куски также образуют непрерывный сектор. Для каждого непрерывного сектора найдем его угол, то есть сумму углов кусков входящих в него. Если угол одного сектора равен x, то разница углов секторов равна |x - (360 - x)| = |2 * x - 360| = 2 * |x - 180|. Переберем сектор, зная его угол x обновим ответ.
Асимптотика O(n2) или O(n).
895B - XK Segments
Для начала узнаем, как посчитать количество чисел на отрезке делящихся на x. Пусть левая граница отрезка это l, а правая r. Тогда количество чисел делящихся нацело на x и принадлежащих [l, r] равно r/x – (l-1)/x. Отсортируем массив a по возрастанию. Переберем левую границу отрезка, пусть это a[i]. Тогда на роль правой границы подходят все числа a[j] такие, что a[j] / x–(a[i] - 1) / x = k. Значение (a[i] - 1) / x мы знаем, а a[j] / x монотонно возрастает при возрастающем a[j]. То есть можно сделать бинарный поиск по отсортированному массиву, который найдет индексы минимального и максимального подходящего a[j], а значит и их количество.
Асимптотика O(n * log(n)).
895C - Square Subsets
Заметим, что число x является квадратом некоторого натурального числа <=> в разложение x на простые множители каждое простое число входит четное количество раз. Простых чисел меньших 70 всего 19. Посчитаем битмаску для каждого из чисел от 1 до 70 по следующему принципу: В битовом представлении маски в разряде k стоит 1, если k-ое простое число входит в разложение этого числа нечетное количество раз. Иначе 0. Для каждого различного значения a[i] нас на самом деле интересует только войдет оно четное количество раз в произведение или нечетное. Пусть f1[i], f0[i] это количество способов взять из a нечетное и четное количество чисел i соответственно. Будем считать динамику по битмаскам. Обозначим за dp[i][j] количество способов выбрать некоторые элементы массива <= i таким образом, чтобы в их произведении в нечетных степенях содержались только те простые числа, на месте порядкового номера которых в битовом представлении j стоит 1. Изначально dp[0][0] = 1. Переходы следующие:
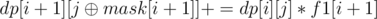
dp[i + 1][j] + = dp[i][j] * f0[i + 1]
Тогда ответ это dp[70][0].
Асимптотика O(max*2^cnt(max)), где max максимальное значение a[i], а cnt(max) количество простых чисел не больших max.
895D - String Mark
Пусть мы умеем вычислять функцию f(s) равную количеству перестановок строки a строго меньших s. Тогда ответ равен f(b) - f(a)–1. Теперь надо научиться находить значение f(s). Посчитаем количество вхождений каждой буквы в строку a – cnt[26]. Будем перебирать позицию первого различного символа в перестановке a и строке s и обновлять количество оставшихся символов cnt[26]. Для каждой такой позиции переберем символ в перестановке a который будет стоять на этой позиции. Он должен быть меньше символа на этой позиции в строке s. Для каждой такой ситуации надо вычислить и прибавить к ответу количество различных перестановок которые можно получить используя не задействованные на данный момент символы. Их количество хранится в cnt[26]. В простейшем виде это решение работает за O(n * k2), где k размер алфавита. Такое решение не проходит тесты, но его можно оптимизировать до O(n * k), что уже проходит по времени.
Асимптотика O(n * k), где k размер алфавита.
895E - Eyes Closed
Будем поддерживать для каждой позиции математическое ожидание значения на ней. Изначально для позиции i оно равно a[i]. Пусть надо обработать запрос первого типа. Каждое число из отрезка [l1, r1] останется на своем месте с вероятностью (r1–l1) / (r1–l1 + 1). Вероятность того, что оно будет заменено числом из [l2, r2] равна 1 / (r1 - l1 + 1). Математическое ожидание числа, на которое оно будет заменено есть среднее арифметическое математических ожидании чисел в [l2, r2], обозначим его за x. Тогда чтобы обновить матожидание числа из [l1, r1] надо умножить его на (r1–l1) / (r1–l1 + 1) и прибавить x / (r1–l1 + 1). То есть запрос первого типа сводится к запросу домножить все числа на отрезке и прибавить к ним число. Чтобы обработать второй запрос надо находить сумму чисел на отрезке. Все эти запросы можно обрабатывать деревом отрезков.
Асимптотика O(n + q * log(n)).










