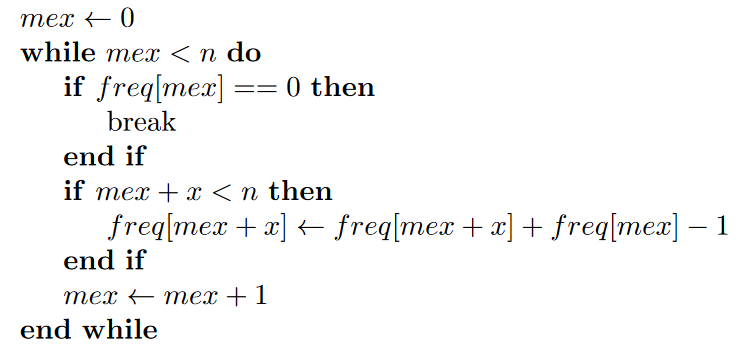Hello fellow Codeforcers ! I took part in Codeforces Round 981 (Div. 3) on last Friday. I didn't have a Div. 3 contest in a long time, so I was eager to participate. I didn't like the round so much, because I felt it relied too much on implementation rather than problem solving. I was able to find the theoretical solution for A-F during the contest, but I couldn't implement successfully D-F in real time. Having a better understanding of what I missed could get me a huge improve in future contests.
This is why I share here is my thoughts and solutions about the first 6 problems of the contest. Welcome to my humble green editorial !
2033A - Sakurako and Kosuke
We want to find the parity of the last $$$k$$$ s.t. $$$|S_k|\leq n \implies k \leq n$$$, i.e. the parity of $$$n$$$. If $$$n\%2$$$, Kosuke plays the last turn, else it is Sakurako.
Complexity
$$$\mathcal{O}(1)$$$ complexity
What I've learnt
Not much, Div. 3 A problem, focus on pattern identification.
2033B - Sakurako and Water
Observation : When defining a square to increase one value on its diagonal, it's always better to consider the largest square possible increasing it.
The formalism here is boring and I think it doesn't really help to understand the solution. At each operation, one can increase all values in the same "diagonal" of the matrix by 1 by choosing the largest possible squares for each "diagonal". The answer is to find the sum of the maximum over all matrix "diagonals".
Complexity
You'll end up iterating over all values in a specific order. $$$\mathcal{O}(n^2)$$$ complexity.
What I've learnt
Not much, problem statement was misleading for me, and the only difficulty is the implementation.
2033C - Sakurako's Field Trip
I read many unhappy comments on C, and during the contest, less people succeeded at it than D. I felt it wasn't a hard problem at all, which means I must be improving :D .
Observation : The participation to the disturbance of each pair of $$$(i, n-i+1)$$$ can be decided only based on the previous pair $$$(i-1, n-(i-1)+1)$$$
This leads to consider pairs iteratively, starting from the middle pair (or middle point) of the array. For the $$$i$$$-th pair $$$(i, n-i+1)$$$, regardless of the positioning of the $$$(i-1)$$$-th pair, you can always swap it or not to get the minimal disturbance amount.
Complexity
Iterating over values in $$$a$$$ results in $$$\mathcal{O}(n)$$$ complexity overall.
What I've learnt
This was an easy problem in my opinion, but nothing surprising for a Div. 3 C problem.
2033D - Kousuke's Assignment
Here comes my big frustration. During the contest, I found the statement misleading, since there may be many way to chose beautiful segments. Once I got my head wrapped around it, the idea for this problem stroke me as pretty simple.
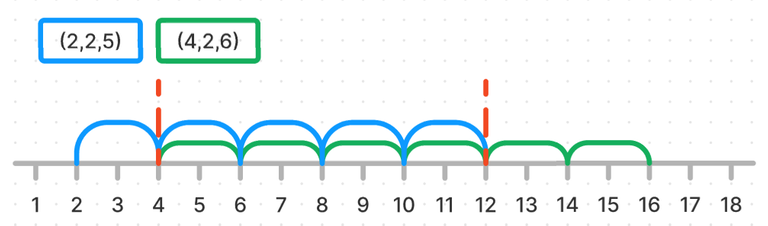
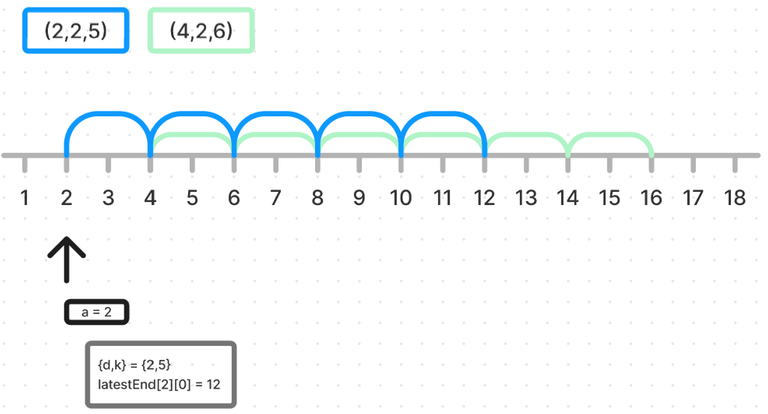
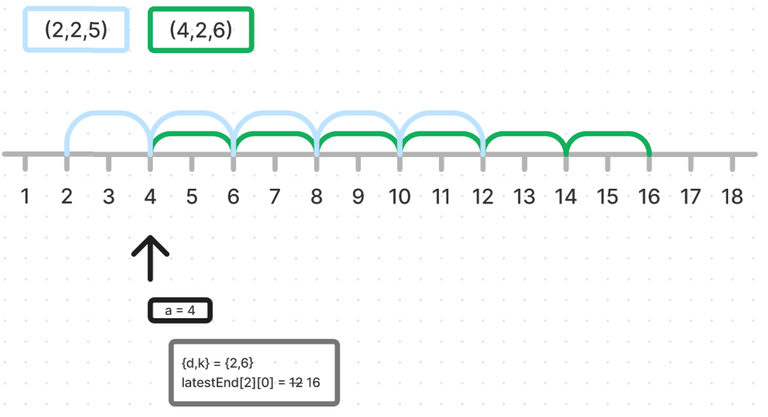
For any two positions $$$i < j$$$, if $$$pref[i] == pref[j]$$$, then $$$(i+1,j)$$$ is a beautiful segment. To find the maximum number of such segments, one should consider greedily the shortest possible segments. This can be done by iterating of $$$i$$$ and store the prefixes met. If the current prefix has been seen after the last beautiful segment has been found, a new shortest non-overlapping beautiful segment can be considered.
The loop is in $$$\mathcal{O}(n)$$$, and I used a $$$unordered_set$$$ to insert and search elements in $$$\mathcal{O}(1)$$$.
During the contest, I got WA (on 530-th value of test 2 ...) because I wasn't careful enough on handling beautiful segments with ends in $$$1$$$ or $$$n$$$.
I came back after the contest, and wrote correct code, this time getting TLE on test 18. My solution seems correct and I didn't know how to optimize it.
Looking at others submissions, I came across this submission(TLE) and this one(Accepted) by avi032904, between which he changed from an unordered_set to a set. I did some more research and found this blog by neal. I highly encourage you to read it, I'll summarize here the main ideas.
For insertion operations on an unordered_map to be in $$$\mathcal{O}(1)$$$ time complexity, the average number of collisions for each item should be $$$\mathcal{O}(1)$$$ on average. This is most likely always true in an context where items at selected at random. Now, in a hacking context, knowing the hash function of the unordered_map, one can deliberately cause as much collisions as possible and make insertion a $$$\mathcal{O}(n^2)$$$ operation.
An approach is to reintroduce unpredicability by using a precise clock and some arithmetic operations to prevent targeted attacks on modular key values. The detailed explanation is to read on neal's blog.
This allows my code to pass all tests.
Complexity
The code only performs one prefix sum on the whole array and perform basic operations on an unordered_map, resulting in an overall $$$\mathcal{O}(n)$$$ complexity.
What I've learnt
In some (hacking) contexts, things I held to be always true (insertion in $$$\mathcal{O}(1)$$$) can outcome being proven wrong. When facing such situations, one must be ready to look into a new level of complexity and understand in depth the related concepts. I'll definitely remember this one.
2033E - Sakurako, Kosuke, and the Permutation
This is not the first time I see a problem about permutations with an operation involving $$$p_{p_i}$$$. I should remember the following observations. My editorial is very similar to the official from FBI :
My idea during the contest was to suppose that one was always able to break a cycle of size $$$k$$$ into two cycles of size $$$\frac{k}{2}$$$ and $$$\frac{k}{2}+(k\%2)$$$. I used a recursive function and memoization to get the statement tests right, but got WA on testcase 2.
My assumption and my implementation were correct, but it doesn't yield the optimal answer. A better assumption is that is is always possible to perform a swap to create 2-cycles iteratively.
A cycle of size $$$n$$$ needs $$$\lfloor \frac{k-1}{2} \rfloor$$$ operations to create a valid subsequence in the permutation.
Complexity
Detecting all cycles is in $$$\mathcal{O}(n)$$$ and each can be handled independently, resulting in an overall $$$\mathcal{O}(n)$$$ complexity.
What I've learnt
My first assumption was suboptimal, and I failed at realizing it in time. This lead me to prove the result used in the problem, I'll probably have use for this later.
2033F - Kosuke's Sloth
This problem is definitely built like a Project Euler problem, which is not to my displeasure. I took some 30 minutes during the contest to think about this, and I must say that I came pretty close. I submitted an accepted solution short after the end of the contest, which I already see as a win.
I got the intuition that Fibonacci modulo $$$k$$$ was periodic. My approach was then to compute the first complete period and store the positions of zeros in an array $$$zeros$$$. The answer can be found by taking computing $$$\lfloor \frac{n}{size(z)} \rfloor$$$ to know the number of complete periods before $$$n$$$, and consider the right element in $$$zeros$$$.
With more research and the official editorial, I learnt more properties about the Fibonacci sequence :
The Fibonacci modulo $$$n$$$ is called Pisano period and writes $$$\pi(n)$$$.
$$$gcd(F_n, F_m) = F_{gcd(n,m)}$$$. This leads to $$$gcd(F_i, F_{i*j}) = F_i$$$ and finally $$$F_i | F_{i*j}$$$
We can show that zeros in the period cycle are evenly spaced. $$$F(0) = 0$$$, we can skip it. If we denote $$$i$$$ the smallest natural integer such that $$$F(i) \equiv 0 [n]$$$, all others zeros will be at indices $$$i*j$$$.
The simplest solution is to look for $$$i$$$ and consider $$$i*n$$$.
Complexity
It appears that $$$\pi(k) \leq 6*k$$$ the resulting complexity is then $$$\mathcal{O}(k)$$$
What I've learnt
I really liked this type of problem. I have a computer science and mathematics background, so I should be able to be good at this type of problems. I will definitely try to remember these properties on Fibonacci (as well as the proof).
Conclusion
I have less time currently to write these custom editorials and I apologize for there is less preparation. I think it still allows me to better learn from contests and maybe share some thoughts with other participants. I really liked the problems and learnt many very useful things on maps, Fibonacci and others. Thank you again FBI, Vladosiya and all other involved in the contest organization (Parag_AP for green testing :)) and once again MikeMirzayanov for creating Codeforces and Polygon.
See you soon for my next editorial, this time with more graphics I promise.