CodeChef invites you to participate in the May Cook-off 2015 at http://www.codechef.com/COOK58. The CodeChef May Cook-Off 2015 is an especial contest dedicated to our beloved community member Harsha Suryanarayana, whose sudden demise last year left us all in shock. Harsha, was an inspiration to many and he remains so. On his birthday, 23rd May let’s come together and do what Harsha liked the most and that is to have a fun filled competitive contest. So, do join us for the May Cook-Off 2015 to pay homage to one of finest and respected community member. You will always be with us humblefool.
Time: 24nd May 2015 (2130 hrs) to 25rd May 2015 (0000 hrs). (Indian Standard Time — +5:30 GMT) — Check your timezone.
Details: http://www.codechef.com/COOK58
Registration: Just need to have a CodeChef user id to participate.
New users please register here
- Problem Setters : RedAnt (Anil Kishore) and PraveenDhinwa (Praveen Dhinwa)
- Editorialist: Balajiganapathi (Balajiganapathi)
- Problem Tester: utkarshl (Utkarsh Lath)
- Russian Translator : CherryTree (Sergey Kulik)
- Mandarin Translator: gediiiiiii (Gedi Zheng)
- Contest Admin: PraveenDhinwa (Praveen Dhinwa)
It promises to deliver on an interesting set of algorithmic problems with something for all.
The contest is open for all and those, who are interested, are requested to have a CodeChef userid, in order to participate.









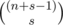 .
.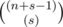 % p. As
% p. As 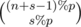 .
.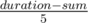 songs.
songs.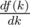 = — (# of elements of b > k) + (# of elements of a < k)
= — (# of elements of b > k) + (# of elements of a < k)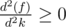
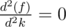 at the event points (or the points of array a and b).
at the event points (or the points of array a and b).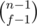 .
.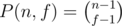
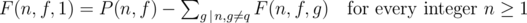
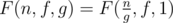 .
.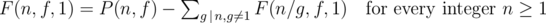
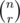 .
.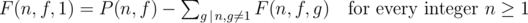
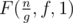 .
.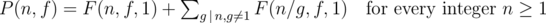
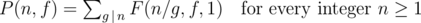
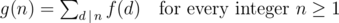
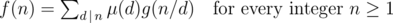
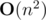 , Can anybody give a better solution than this?
, Can anybody give a better solution than this?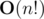 .
.
