Всем привет! :)
На случай, если вы пропустили рассылку, сообщаем, что сегодня в 10:00 UTC +3 стартовал второй раунд Оптимизационного трека. Как и первый раунд, он продлится 7 дней. Вам предложена одна задача, которая не предполагает наличие полного решения, но допускает множество подходов. По результатам двух раундов (смотрите раздел 3 в https://contest.yandex.ru/algorithm2018/rules/ — правила суммирования раундов одинаковы для алгоритмического и оптимизационного треков) будут определены победители трека и 128 будущих обладателей футболок с символикой конкурса.
Мы подготовили для вас задачу, которая симулирует работу поискового робота. Предлагаем вам ощутить на себе сложности индексации сайтов и постараться оптимизировать обход интернета — это всего лишь одна из задач, которую в Яндексе решают разработчики. Разумеется, задача была достаточно сильно упрощена, поскольку на её решение у вас всего неделя, но сможете ли вы научиться назначать сайты роботам достаточно оптимально?
Регистрация на конкурс еще открыта, так что всё в ваших руках — удачи!










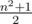 . Несложно убедиться, что на квадратное поле со стороной
. Несложно убедиться, что на квадратное поле со стороной 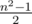 "доминошек"
"доминошек" 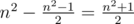 .
.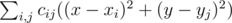 принимает минимальное возможное значение. Эту величину можно преобразовать к виду
принимает минимальное возможное значение. Эту величину можно преобразовать к виду 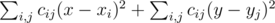 , и заметить, что поскольку левая часть не зависит от
, и заметить, что поскольку левая часть не зависит от 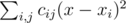 , вторая минимизируется аналогично. Поскольку выражение в скобках не зависит от
, вторая минимизируется аналогично. Поскольку выражение в скобках не зависит от 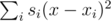 , где
, где 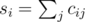 . Теперь достаточно просто перебрать все возможные значения
. Теперь достаточно просто перебрать все возможные значения 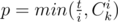 чисел с
чисел с 
