1. Одежда (A Div-2)
2. Сумма цифр (B Div-2)
3. Домашнее задание (C Div-2, A Div-1)
4. Автобусы (D Div-2, B Div-1)
5. Вектора (E Div-2, C Div-1)
6. Замок (D Div-1)
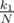 клад окажется в первом поддереве. Тогда среднее время нахождения клада будет t1.
клад окажется в первом поддереве. Тогда среднее время нахождения клада будет t1.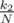 клад окажется во втором поддереве. Тогда среднее время нахождения клада будет T1 + t2.
клад окажется во втором поддереве. Тогда среднее время нахождения клада будет T1 + t2.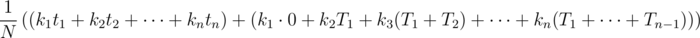
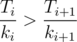 .
.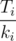 , иначе найдется пара соседних поддеревьев, замена местами которых приведёт к улучшению результата. Таким образом, надо отсортировать поддеревья по этой величине, и обходить их этом порядке.
, иначе найдется пара соседних поддеревьев, замена местами которых приведёт к улучшению результата. Таким образом, надо отсортировать поддеревья по этой величине, и обходить их этом порядке.7. Конфеты и Камни. (E Div-1)
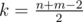 . Какие клетки поля могут быть k-тыми? Очевидно, те, у которых сумма координат равна k, то есть, это будет диагональ прямоугольника. Поэтому очевидно, что несложно динамикой за O(nm) в нижнем треугольнике под этой диагональю посчитать, какое какую максимальную сумму можно набрать, придя в каждую из клеток этой диагонали. Аналогичной динамикой в верхнем треугольнике (на это раз сверху вниз) для каждой клетки на этой диагонали посчитаем, какую максимальную сумму можно собрать, стартовав с этой клетки. Сложив эти две величины, получим, какую максимальную сумму можно получить, пройдя через эту клетку. Осталось найти клетку (x, y), в которой достигается максимум. Её мы и возьмем за k-тую клетку нашего пути. Заметим, что в течение этой итерации мы использовали O((n + m)2) времени и O(n + m) памяти.
. Какие клетки поля могут быть k-тыми? Очевидно, те, у которых сумма координат равна k, то есть, это будет диагональ прямоугольника. Поэтому очевидно, что несложно динамикой за O(nm) в нижнем треугольнике под этой диагональю посчитать, какое какую максимальную сумму можно набрать, придя в каждую из клеток этой диагонали. Аналогичной динамикой в верхнем треугольнике (на это раз сверху вниз) для каждой клетки на этой диагонали посчитаем, какую максимальную сумму можно собрать, стартовав с этой клетки. Сложив эти две величины, получим, какую максимальную сумму можно получить, пройдя через эту клетку. Осталось найти клетку (x, y), в которой достигается максимум. Её мы и возьмем за k-тую клетку нашего пути. Заметим, что в течение этой итерации мы использовали O((n + m)2) времени и O(n + m) памяти.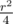 . На третьем - 4 раза по
. На третьем - 4 раза по 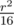 , и так далее. Все будет потрачено времени
, и так далее. Все будет потрачено времени 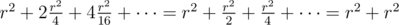 . Таким образом, описанное решение занимает O((n + m)2) времени и очевидно, что оно занимает O(n + m) памяти.
. Таким образом, описанное решение занимает O((n + m)2) времени и очевидно, что оно занимает O(n + m) памяти.









