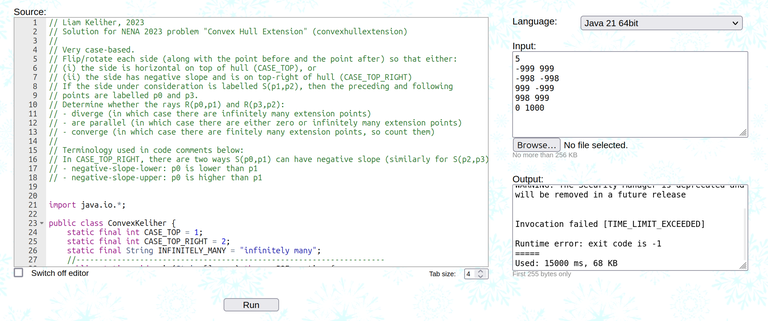
For years, I have been dissuading people from using random vector in C++ unless it is necessary (like in adjacency lists, where otherwise it is very annoying to implement). The most common response I get is
BuT iT'S sO eAsY tO uSe!
Recently I finally had a prime example of why all these syntactic sugar will give you a sweet tooth. Witness Collect the Coins, a problem from the recent UCup contest.
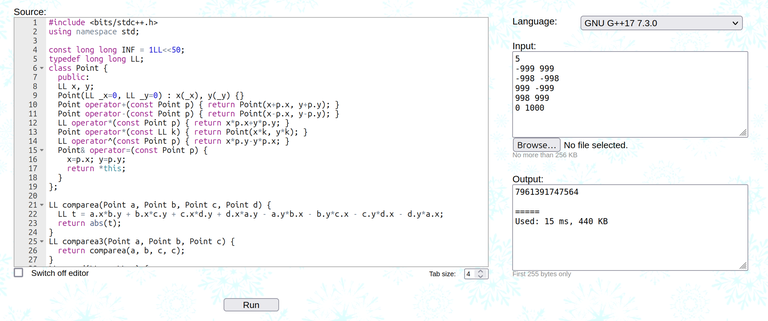
The code we had in contest got TLE'ed:
Code
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int maxn = 1e6 + 100;
ll n;
pair<ll, ll> vec[maxn];
bool check(ll V) {
vector<bool> dp(n + 1);
multiset<pair<ll, ll>> all;
auto valid = [&](ll i, ll j) {
auto [t1, p1] = vec[i];
auto [t2, p2] = vec[j];
return abs(p1 - p2) <= abs(t1 - t2) * V;
};
auto insert = [&](ll pos) {
auto [t, p] = vec[pos];
// insert (p - tV, -p-tV)
// ...
auto x = p - t * V;
auto y = -p - t * V;
while (all.size()) {
auto it = all.lower_bound({x + 1, -3e18});
if (it == all.begin()) break;
auto [tx, ty] = *(--it);
if (ty <= y) all.extract({tx, ty});
}
bool flag = true;
if (all.size()) {
auto rit = all.lower_bound({x, y});
if (rit == all.end())
flag = true;
else {
auto [tx, ty] = *rit;
if (ty < y)
flag = true;
else
flag = false;
}
}
if (flag) all.insert({x, y});
};
for (int i = 2; i < n; i++) {
if (!valid(i - 1, i)) break;
dp[i + 1] = true;
}
// check st = 2, i = 3?
dp[2] = true;
for (ll i = 3; i <= n; i++) {
if (!valid(i - 2, i - 1)) {
all.clear();
}
// cout << "addr2" << endl;
if (dp[i - 1]) insert(i - 2);
// j-1
auto [qt, qp] = vec[i];
auto qx = qp - qt * V;
auto qy = -qp - qt * V;
auto it = all.lower_bound({qx, qy});
if (it != all.end()) {
auto [tx, ty] = *it;
if (ty >= qy) dp[i] = true;
}
}
for (int temp = n; temp >= 1; temp--) {
if (temp < n and !valid(temp, temp + 1)) break;
if (dp[temp]) return true;
}
return false;
};
void solve() {
cin >> n;
for (ll i = 1; i <= n; i++) {
cin >> vec[i].first >> vec[i].second;
}
unordered_set<ll> all_pos;
for (ll i = 1; i <= n; i++) {
all_pos.insert(vec[i].second);
}
if (all_pos.size() <= 2) {
cout << 0 << '\n';
return;
}
ll L = 1, R = 1e9 + 100;
while (L < R) {
ll mid = (L + R) / 2;
if (check(mid))
R = mid;
else
L = mid + 1;
}
if (L > 1e9) L = -1;
cout << L << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
ll t;
cin >> t;
while (t--) {
solve();
}
return 0;
}
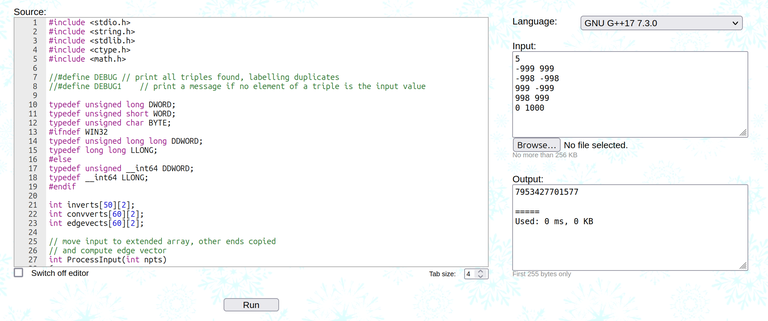
However, just doing these three things is enough for AC:
- Move all data structure variables to global;
- Move all closures to functions;
- Last but not the least, stop using random vectors.
Code
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int maxn = 1e6 + 100;
ll n;
pair<ll, ll> vec[maxn];
set<pair<ll, ll>> all;
unordered_set<ll> all_pos;
ll V;
bool valid(ll i, ll j) {
auto [t1, p1] = vec[i];
auto [t2, p2] = vec[j];
return abs(p1 - p2) <= abs(t1 - t2) * V;
}
void insert(ll pos) {
auto [t, p] = vec[pos];
// insert (p - tV, -p-tV)
// ...
auto x = p - t * V;
auto y = -p - t * V;
bool flag = true;
auto rit = all.lower_bound({x, y});
if (rit == all.end())
flag = true;
else {
auto [tx, ty] = *rit;
if (ty < y)
flag = true;
else
flag = false;
}
if (flag) {
auto it = rit;
while (it != all.begin()) {
auto pit = prev(it, 1);
auto [tx, ty] = *pit;
if (ty <= y)
all.erase(pit);
else
break;
}
all.insert({x, y});
}
}
bool check() {
static bool dp[maxn];
std::fill(dp, dp + n + 1, 0);
all.clear();
for (int i = 2; i < n; i++) {
if (!valid(i - 1, i)) break;
dp[i + 1] = true;
}
// check st = 2, i = 3?
dp[2] = true;
for (ll i = 3; i <= n; i++) {
if (!valid(i - 2, i - 1)) {
all.clear();
}
// cout << "addr2" << endl;
if (dp[i - 1]) insert(i - 2);
// j-1
auto [qt, qp] = vec[i];
auto qx = qp - qt * V;
auto qy = -qp - qt * V;
auto it = all.lower_bound({qx, qy});
if (it != all.end()) {
auto [tx, ty] = *it;
if (ty >= qy) dp[i] = true;
}
}
for (int temp = n; temp >= 1; temp--) {
if (temp < n and !valid(temp, temp + 1)) break;
if (dp[temp]) return true;
}
return false;
};
void solve() {
cin >> n;
for (ll i = 1; i <= n; i++) {
cin >> vec[i].first >> vec[i].second;
}
all_pos.clear();
for (ll i = 1; i <= n; i++) {
all_pos.insert(vec[i].second);
}
if (all_pos.size() <= 2) {
cout << 0 << '\n';
return;
}
ll L = 1, R = 1e9 + 100;
while (L < R) {
ll mid = (L + R) / 2;
V = mid;
if (check())
R = mid;
else
L = mid + 1;
}
if (L > 1e9) L = -1;
cout << L << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
ll t;
cin >> t;
while (t--) {
solve();
}
return 0;
}
Surely everyone will stop using random vectors instead of...
BuT mY tEaMmAtE wIlL hElP mE wItH tHe CoNsTaNtS!
Ugh for the love of...